
- •Preface
- •Introduction
- •1.1 Spatial coordinate systems
- •1.2 Sound fields and their physical characteristics
- •1.2.1 Free-field and sound waves generated by simple sound sources
- •1.2.2 Reflections from boundaries
- •1.2.3 Directivity of sound source radiation
- •1.2.4 Statistical analysis of acoustics in an enclosed space
- •1.2.5 Principle of sound receivers
- •1.3 Auditory system and perception
- •1.3.1 Auditory system and its functions
- •1.3.2 Hearing threshold and loudness
- •1.3.3 Masking
- •1.3.4 Critical band and auditory filter
- •1.4 Artificial head models and binaural signals
- •1.4.1 Artificial head models
- •1.4.2 Binaural signals and head-related transfer functions
- •1.5 Outline of spatial hearing
- •1.6 Localization cues for a single sound source
- •1.6.1 Interaural time difference
- •1.6.2 Interaural level difference
- •1.6.3 Cone of confusion and head movement
- •1.6.4 Spectral cues
- •1.6.5 Discussion on directional localization cues
- •1.6.6 Auditory distance perception
- •1.7 Summing localization and spatial hearing with multiple sources
- •1.7.1 Summing localization with two sound sources
- •1.7.2 The precedence effect
- •1.7.3 Spatial auditory perceptions with partially correlated and uncorrelated source signals
- •1.7.4 Auditory scene analysis and spatial hearing
- •1.7.5 Cocktail party effect
- •1.8 Room reflections and auditory spatial impression
- •1.8.1 Auditory spatial impression
- •1.8.2 Sound field-related measures and auditory spatial impression
- •1.8.3 Binaural-related measures and auditory spatial impression
- •1.9.1 Basic principle of spatial sound
- •1.9.2 Classification of spatial sound
- •1.9.3 Developments and applications of spatial sound
- •1.10 Summary
- •2.1 Basic principle of a two-channel stereophonic sound
- •2.1.1 Interchannel level difference and summing localization equation
- •2.1.2 Effect of frequency
- •2.1.3 Effect of interchannel phase difference
- •2.1.4 Virtual source created by interchannel time difference
- •2.1.5 Limitation of two-channel stereophonic sound
- •2.2.1 XY microphone pair
- •2.2.2 MS transformation and the MS microphone pair
- •2.2.3 Spaced microphone technique
- •2.2.4 Near-coincident microphone technique
- •2.2.5 Spot microphone and pan-pot technique
- •2.2.6 Discussion on microphone and signal simulation techniques for two-channel stereophonic sound
- •2.3 Upmixing and downmixing between two-channel stereophonic and mono signals
- •2.4 Two-channel stereophonic reproduction
- •2.4.1 Standard loudspeaker configuration of two-channel stereophonic sound
- •2.4.2 Influence of front-back deviation of the head
- •2.5 Summary
- •3.1 Physical and psychoacoustic principles of multichannel surround sound
- •3.2 Summing localization in multichannel horizontal surround sound
- •3.2.1 Summing localization equations for multiple horizontal loudspeakers
- •3.2.2 Analysis of the velocity and energy localization vectors of the superposed sound field
- •3.2.3 Discussion on horizontal summing localization equations
- •3.3 Multiple loudspeakers with partly correlated and low-correlated signals
- •3.4 Summary
- •4.1 Discrete quadraphone
- •4.1.1 Outline of the quadraphone
- •4.1.2 Discrete quadraphone with pair-wise amplitude panning
- •4.1.3 Discrete quadraphone with the first-order sound field signal mixing
- •4.1.4 Some discussions on discrete quadraphones
- •4.2 Other horizontal surround sounds with regular loudspeaker configurations
- •4.2.1 Six-channel reproduction with pair-wise amplitude panning
- •4.2.2 The first-order sound field signal mixing and reproduction with M ≥ 3 loudspeakers
- •4.3 Transformation of horizontal sound field signals and Ambisonics
- •4.3.1 Transformation of the first-order horizontal sound field signals
- •4.3.2 The first-order horizontal Ambisonics
- •4.3.3 The higher-order horizontal Ambisonics
- •4.3.4 Discussion and implementation of the horizontal Ambisonics
- •4.4 Summary
- •5.1 Outline of surround sounds with accompanying picture and general uses
- •5.2 5.1-Channel surround sound and its signal mixing analysis
- •5.2.1 Outline of 5.1-channel surround sound
- •5.2.2 Pair-wise amplitude panning for 5.1-channel surround sound
- •5.2.3 Global Ambisonic-like signal mixing for 5.1-channel sound
- •5.2.4 Optimization of three frontal loudspeaker signals and local Ambisonic-like signal mixing
- •5.2.5 Time panning for 5.1-channel surround sound
- •5.3 Other multichannel horizontal surround sounds
- •5.4 Low-frequency effect channel
- •5.5 Summary
- •6.1 Summing localization in multichannel spatial surround sound
- •6.1.1 Summing localization equations for spatial multiple loudspeaker configurations
- •6.1.2 Velocity and energy localization vector analysis for multichannel spatial surround sound
- •6.1.3 Discussion on spatial summing localization equations
- •6.1.4 Relationship with the horizontal summing localization equations
- •6.2 Signal mixing methods for a pair of vertical loudspeakers in the median and sagittal plane
- •6.3 Vector base amplitude panning
- •6.4 Spatial Ambisonic signal mixing and reproduction
- •6.4.1 Principle of spatial Ambisonics
- •6.4.2 Some examples of the first-order spatial Ambisonics
- •6.4.4 Recreating a top virtual source with a horizontal loudspeaker arrangement and Ambisonic signal mixing
- •6.5 Advanced multichannel spatial surround sounds and problems
- •6.5.1 Some advanced multichannel spatial surround sound techniques and systems
- •6.5.2 Object-based spatial sound
- •6.5.3 Some problems related to multichannel spatial surround sound
- •6.6 Summary
- •7.1 Basic considerations on the microphone and signal simulation techniques for multichannel sounds
- •7.2 Microphone techniques for 5.1-channel sound recording
- •7.2.1 Outline of microphone techniques for 5.1-channel sound recording
- •7.2.2 Main microphone techniques for 5.1-channel sound recording
- •7.2.3 Microphone techniques for the recording of three frontal channels
- •7.2.4 Microphone techniques for ambience recording and combination with frontal localization information recording
- •7.2.5 Stereophonic plus center channel recording
- •7.3 Microphone techniques for other multichannel sounds
- •7.3.1 Microphone techniques for other discrete multichannel sounds
- •7.3.2 Microphone techniques for Ambisonic recording
- •7.4 Simulation of localization signals for multichannel sounds
- •7.4.1 Methods of the simulation of directional localization signals
- •7.4.2 Simulation of virtual source distance and extension
- •7.4.3 Simulation of a moving virtual source
- •7.5 Simulation of reflections for stereophonic and multichannel sounds
- •7.5.1 Delay algorithms and discrete reflection simulation
- •7.5.2 IIR filter algorithm of late reverberation
- •7.5.3 FIR, hybrid FIR, and recursive filter algorithms of late reverberation
- •7.5.4 Algorithms of audio signal decorrelation
- •7.5.5 Simulation of room reflections based on physical measurement and calculation
- •7.6 Directional audio coding and multichannel sound signal synthesis
- •7.7 Summary
- •8.1 Matrix surround sound
- •8.1.1 Matrix quadraphone
- •8.1.2 Dolby Surround system
- •8.1.3 Dolby Pro-Logic decoding technique
- •8.1.4 Some developments on matrix surround sound and logic decoding techniques
- •8.2 Downmixing of multichannel sound signals
- •8.3 Upmixing of multichannel sound signals
- •8.3.1 Some considerations in upmixing
- •8.3.2 Simple upmixing methods for front-channel signals
- •8.3.3 Simple methods for Ambient component separation
- •8.3.4 Model and statistical characteristics of two-channel stereophonic signals
- •8.3.5 A scale-signal-based algorithm for upmixing
- •8.3.6 Upmixing algorithm based on principal component analysis
- •8.3.7 Algorithm based on the least mean square error for upmixing
- •8.3.8 Adaptive normalized algorithm based on the least mean square for upmixing
- •8.3.9 Some advanced upmixing algorithms
- •8.4 Summary
- •9.1 Each order approximation of ideal reproduction and Ambisonics
- •9.1.1 Each order approximation of ideal horizontal reproduction
- •9.1.2 Each order approximation of ideal three-dimensional reproduction
- •9.2 General formulation of multichannel sound field reconstruction
- •9.2.1 General formulation of multichannel sound field reconstruction in the spatial domain
- •9.2.2 Formulation of spatial-spectral domain analysis of circular secondary source array
- •9.2.3 Formulation of spatial-spectral domain analysis for a secondary source array on spherical surface
- •9.3 Spatial-spectral domain analysis and driving signals of Ambisonics
- •9.3.1 Reconstructed sound field of horizontal Ambisonics
- •9.3.2 Reconstructed sound field of spatial Ambisonics
- •9.3.3 Mixed-order Ambisonics
- •9.3.4 Near-field compensated higher-order Ambisonics
- •9.3.5 Ambisonic encoding of complex source information
- •9.3.6 Some special applications of spatial-spectral domain analysis of Ambisonics
- •9.4 Some problems related to Ambisonics
- •9.4.1 Secondary source array and stability of Ambisonics
- •9.4.2 Spatial transformation of Ambisonic sound field
- •9.5 Error analysis of Ambisonic-reconstructed sound field
- •9.5.1 Integral error of Ambisonic-reconstructed wavefront
- •9.5.2 Discrete secondary source array and spatial-spectral aliasing error in Ambisonics
- •9.6 Multichannel reconstructed sound field analysis in the spatial domain
- •9.6.1 Basic method for analysis in the spatial domain
- •9.6.2 Minimizing error in reconstructed sound field and summing localization equation
- •9.6.3 Multiple receiver position matching method and its relation to the mode-matching method
- •9.7 Listening room reflection compensation in multichannel sound reproduction
- •9.8 Microphone array for multichannel sound field signal recording
- •9.8.1 Circular microphone array for horizontal Ambisonic recording
- •9.8.2 Spherical microphone array for spatial Ambisonic recording
- •9.8.3 Discussion on microphone array recording
- •9.9 Summary
- •10.1 Basic principle and implementation of wave field synthesis
- •10.1.1 Kirchhoff–Helmholtz boundary integral and WFS
- •10.1.2 Simplification of the types of secondary sources
- •10.1.3 WFS in a horizontal plane with a linear array of secondary sources
- •10.1.4 Finite secondary source array and effect of spatial truncation
- •10.1.5 Discrete secondary source array and spatial aliasing
- •10.1.6 Some issues and related problems on WFS implementation
- •10.2 General theory of WFS
- •10.2.1 Green’s function of Helmholtz equation
- •10.2.2 General theory of three-dimensional WFS
- •10.2.3 General theory of two-dimensional WFS
- •10.2.4 Focused source in WFS
- •10.3 Analysis of WFS in the spatial-spectral domain
- •10.3.1 General formulation and analysis of WFS in the spatial-spectral domain
- •10.3.2 Analysis of the spatial aliasing in WFS
- •10.3.3 Spatial-spectral division method of WFS
- •10.4 Further discussion on sound field reconstruction
- •10.4.1 Comparison among various methods of sound field reconstruction
- •10.4.2 Further analysis of the relationship between acoustical holography and sound field reconstruction
- •10.4.3 Further analysis of the relationship between acoustical holography and Ambisonics
- •10.4.4 Comparison between WFS and Ambisonics
- •10.5 Equalization of WFS under nonideal conditions
- •10.6 Summary
- •11.1 Basic principles of binaural reproduction and virtual auditory display
- •11.1.1 Binaural recording and reproduction
- •11.1.2 Virtual auditory display
- •11.2 Acquisition of HRTFs
- •11.2.1 HRTF measurement
- •11.2.2 HRTF calculation
- •11.2.3 HRTF customization
- •11.3 Basic physical features of HRTFs
- •11.3.1 Time-domain features of far-field HRIRs
- •11.3.2 Frequency domain features of far-field HRTFs
- •11.3.3 Features of near-field HRTFs
- •11.4 HRTF-based filters for binaural synthesis
- •11.5 Spatial interpolation and decomposition of HRTFs
- •11.5.1 Directional interpolation of HRTFs
- •11.5.2 Spatial basis function decomposition and spatial sampling theorem of HRTFs
- •11.5.3 HRTF spatial interpolation and signal mixing for multichannel sound
- •11.5.4 Spectral shape basis function decomposition of HRTFs
- •11.6 Simplification of signal processing for binaural synthesis
- •11.6.1 Virtual loudspeaker-based algorithms
- •11.6.2 Basis function decomposition-based algorithms
- •11.7.1 Principle of headphone equalization
- •11.7.2 Some problems with binaural reproduction and VAD
- •11.8 Binaural reproduction through loudspeakers
- •11.8.1 Basic principle of binaural reproduction through loudspeakers
- •11.8.2 Virtual source distribution in two-front loudspeaker reproduction
- •11.8.3 Head movement and stability of virtual sources in Transaural reproduction
- •11.8.4 Timbre coloration and equalization in transaural reproduction
- •11.9 Virtual reproduction of stereophonic and multichannel surround sound
- •11.9.1 Binaural reproduction of stereophonic and multichannel sound through headphones
- •11.9.2 Stereophonic expansion and enhancement
- •11.9.3 Virtual reproduction of multichannel sound through loudspeakers
- •11.10.1 Binaural room modeling
- •11.10.2 Dynamic virtual auditory environments system
- •11.11 Summary
- •12.1 Physical analysis of binaural pressures in summing virtual source and auditory events
- •12.1.1 Evaluation of binaural pressures and localization cues
- •12.1.2 Method for summing localization analysis
- •12.1.3 Binaural pressure analysis of stereophonic and multichannel sound with amplitude panning
- •12.1.4 Analysis of summing localization with interchannel time difference
- •12.1.5 Analysis of summing localization at the off-central listening position
- •12.1.6 Analysis of interchannel correlation and spatial auditory sensations
- •12.2 Binaural auditory models and analysis of spatial sound reproduction
- •12.2.1 Analysis of lateral localization by using auditory models
- •12.2.2 Analysis of front-back and vertical localization by using a binaural auditory model
- •12.2.3 Binaural loudness models and analysis of the timbre of spatial sound reproduction
- •12.3 Binaural measurement system for assessing spatial sound reproduction
- •12.4 Summary
- •13.1 Analog audio storage and transmission
- •13.1.1 45°/45° Disk recording system
- •13.1.2 Analog magnetic tape audio recorder
- •13.1.3 Analog stereo broadcasting
- •13.2 Basic concepts of digital audio storage and transmission
- •13.3 Quantization noise and shaping
- •13.3.1 Signal-to-quantization noise ratio
- •13.3.2 Quantization noise shaping and 1-Bit DSD coding
- •13.4 Basic principle of digital audio compression and coding
- •13.4.1 Outline of digital audio compression and coding
- •13.4.2 Adaptive differential pulse-code modulation
- •13.4.3 Perceptual audio coding in the time-frequency domain
- •13.4.4 Vector quantization
- •13.4.5 Spatial audio coding
- •13.4.6 Spectral band replication
- •13.4.7 Entropy coding
- •13.4.8 Object-based audio coding
- •13.5 MPEG series of audio coding techniques and standards
- •13.5.1 MPEG-1 audio coding technique
- •13.5.2 MPEG-2 BC audio coding
- •13.5.3 MPEG-2 advanced audio coding
- •13.5.4 MPEG-4 audio coding
- •13.5.5 MPEG parametric coding of multichannel sound and unified speech and audio coding
- •13.5.6 MPEG-H 3D audio
- •13.6 Dolby series of coding techniques
- •13.6.1 Dolby digital coding technique
- •13.6.2 Some advanced Dolby coding techniques
- •13.7 DTS series of coding technique
- •13.8 MLP lossless coding technique
- •13.9 ATRAC technique
- •13.10 Audio video coding standard
- •13.11 Optical disks for audio storage
- •13.11.1 Structure, principle, and classification of optical disks
- •13.11.2 CD family and its audio formats
- •13.11.3 DVD family and its audio formats
- •13.11.4 SACD and its audio formats
- •13.11.5 BD and its audio formats
- •13.12 Digital radio and television broadcasting
- •13.12.1 Outline of digital radio and television broadcasting
- •13.12.2 Eureka-147 digital audio broadcasting
- •13.12.3 Digital radio mondiale
- •13.12.4 In-band on-channel digital audio broadcasting
- •13.12.5 Audio for digital television
- •13.13 Audio storage and transmission by personal computer
- •13.14 Summary
- •14.1 Outline of acoustic conditions and requirements for spatial sound intended for domestic reproduction
- •14.2 Acoustic consideration and design of listening rooms
- •14.3 Arrangement and characteristics of loudspeakers
- •14.3.1 Arrangement of the main loudspeakers in listening rooms
- •14.3.2 Characteristics of the main loudspeakers
- •14.3.3 Bass management and arrangement of subwoofers
- •14.4 Signal and listening level alignment
- •14.5 Standards and guidance for conditions of spatial sound reproduction
- •14.6 Headphones and binaural monitors of spatial sound reproduction
- •14.7 Acoustic conditions for cinema sound reproduction and monitoring
- •14.8 Summary
- •15.1 Outline of psychoacoustic and subjective assessment experiments
- •15.2 Contents and attributes for spatial sound assessment
- •15.3 Auditory comparison and discrimination experiment
- •15.3.1 Paradigms of auditory comparison and discrimination experiment
- •15.3.2 Examples of auditory comparison and discrimination experiment
- •15.4 Subjective assessment of small impairments in spatial sound systems
- •15.5 Subjective assessment of a spatial sound system with intermediate quality
- •15.6 Virtual source localization experiment
- •15.6.1 Basic methods for virtual source localization experiments
- •15.6.2 Preliminary analysis of the results of virtual source localization experiments
- •15.6.3 Some results of virtual source localization experiments
- •15.7 Summary
- •16.1.1 Application to commercial cinema and related problems
- •16.1.2 Applications to domestic reproduction and related problems
- •16.1.3 Applications to automobile audio
- •16.2.1 Applications to virtual reality
- •16.2.2 Applications to communication and information systems
- •16.2.3 Applications to multimedia
- •16.2.4 Applications to mobile and handheld devices
- •16.3 Applications to the scientific experiments of spatial hearing and psychoacoustics
- •16.4 Applications to sound field auralization
- •16.4.1 Auralization in room acoustics
- •16.4.2 Other applications of auralization technique
- •16.5 Applications to clinical medicine
- •16.6 Summary
- •References
- •Index

408 Spatial Sound
comparison of Equations (9.4.29) and (9.4.23) indicates that the independent signals of a target plane wave field with directional emphasis are related to those of original plane wave field by following transformation:
S TF S. |
(9.4.30) |
Therefore, directional emphasis in spatial Ambisonic reproduction can be implemented by applying a transformation of Equation (9.4.30) to the Ambisonic-independent signals, or equally, by changing the decoding matrix from [D] to [D′] with [T] = [TF] according to Equation (9.4.5) while keeping the independent signals S unchanged.
The aforementioned analysis of directional emphasis transformation is analogous to the theorem of addition of two angular moments in quantum mechanics (Zeng, 2007; Joshi, 1977). In fact, various symmetric transformations are important issues in modern physics. They are applicable to quantum mechanics, quantum field and particle theory, condensed matter physics, and even acoustics (Schroeder, 1989). Group theory is a useful mathematical tool for symmetric analysis. Gerzon (1973) applied group theory to analyze spatial Ambisonics in his early work. According to group theory (Joshi, 1977), all rotations around z-axis constitute the axial rotation group SO(2); all rotations in a three-dimensional space constitute the threedimensional rotation group SO(3); spatial reflection (inversion) and identity constitute a group S(2) of order 2; SO(3) and S(2) groups constitute the transformation group O(3) in a threedimensional space. The analysis of secondary source arrays for spatial Ambisonics in Section 9.4.1 is similar to that of crystallographic point groups. Short et al. (2007) applied the theory of the special unitary group SU(n) of the degree n to the transformation of multichannel sound signals. Moreover, the directional (beamforming) pattern of driving signals for the first-order Ambisonics with the tetrahedral array of four secondary sources in Figure 6.9 is analogous to electron distribution in a tetrahedral solid (such as silicon); furthermore, the directional pattern of driving signals for the second-order Ambisonics with the array of more secondary sources is analogous to electron distribution in transition metals (Economou, 2006). The discussion in this section shows that the methods in different branches of physics are interchangeable.
9.5 ERROR ANALYSIS OF AMBISONIC-RECONSTRUCTED SOUND FIELD
9.5.1 Integral error of Ambisonic-reconstructed wavefront
Sections 9.3.1 and 9.3.2 indicate that Ambisonics can reconstruct a target plane wave field up to a certain frequency limit and within a circular region centered at the origin. Errors in Ambisonic-reconstructed sound fields involve two parts, i.e., errors caused by approximation in truncating spatial harmonic decomposition of a sound field up to a finite order, and spa- tial-spectral aliasing errors caused by reproduction with discrete and finite secondary source array. The relationship of the errors in Ambisonic-reconstructed sound field, frequency, and size of a region is analyzed in this section.
Bamford and Vanderkooy (1995) suggested using the following (normalized) mean (integral) complex amplitude error of wavefront to evaluate the error in the reconstructed sound field:
|
|
|P r, , f P r, , f |d |
|
|
|
Err1 r, f Err1 kr |
|
. |
(9.5.1) |
||
|
|||||
|
|
||||
|
|
|P r, , f |d |
|
|

Analysis of multichannel sound field recording and reconstruction 409
Equation (9.5.1) is the mean normalized absolute value of errors between the reconstructed pressure amplitude P′(r, θ, f) and the target pressure amplitude P(r, θ, f) over a circle of the receiver position with radius r. For a target incident plane wave with a unit amplitude, the integral in the denominator of Equation (9.5.1) is 2π.
The error in reconstructed sound field can also be evaluated with the following mean square complex amplitude error of wavefront:
|
|
|
|
|
|
|
|
|
|
|
|
Err2 r, f Err2 kr |
|
|
P r, , f P(r, , f ) |
|
2 d |
|
|||||
|
|
|
|||||||||
|
|
|
|
. |
(9.5.2) |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
P r, , f |
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
For a target incident plane wave with a unit amplitude, the integral in the denominator of Equation (9.5.2) is also 2π. The error criteria in Equations (9.5.1) and (9.5.2) are appropriate for arbitrary secondary source arrays and driving signals and not limited to Ambisonics.
For Q-order horizontal far-field Ambisonics, if P(r, θ, f) is a plane wave with a unit amplitude given in Equation (9.3.1), and the reconstructed sound pressure P′(r, θ, f) is a truncation of Equation (9.3.2) up to the Q-order, and the mean square error caused by truncation is calculated from Equation (9.5.2) as
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
2 |
|
|
1 |
|
|
0 |
|
|
|
2 2 |
|
q |
|
|
2 . |
|
Err |
kr |
|
J |
|
|
kr |
|
J |
|
kr |
|
(9.5.3) |
q 1
Errors are independent of the target plane wave direction. When the radius of a region and a wave number satisfies the condition of kr ≤ Q in Equation (9.3.15) for ideal reconstruction, the mean square error expressed in Equation (9.5.3) is less than 0.1 or −10 dB. In this case, a target sound field can be reconstructed accurately (Ward and Abhayapala, 2001).
Discrete arrays with a finite number of secondary sources are used in practical horizontal Ambisonics, which cause mirror spatial spectra and aliasing in driving signals. The overall error in the reconstructed sound field is a mix of truncation errors and spatial-spectral aliasing errors. In Sections 9.3.1 and 9.3.2, driving signals are derived by matching each azimuthal harmonic component of the reconstructed sound field with that of the target sound field up to the Q-order. This operation is equivalent to minimizing the mean square error of the reconstructed sound field in Equation (9.5.2). For example, M secondary sources are arranged uniformly in a horizontal circle and satisfy the condition of M ≥ (2Q + 1), the target sound field is a plane wave with a unit amplitude expressed in Equation (9.3.1), and driving signals are given in Equation (9.3.12). Ambisonic-reconstructed sound pressure is calculated from Equations (9.3.12) and (9.2.14). Then, the mean square error of the reconstructed sound field can be calculated from Equation (9.5.2). However, analytic results are relatively complicated (Poletti, 2000). Instead, some numerical results have been described (Ward and Abhayapala, 2001; Poletti, 2005b).
Figure 9.7 illustrates the mean square errors of the reconstructed sound field for Q = 1-, 2-, and 3-order horizontal Ambisonics with M = 8 secondary sources and the target plane wave from θS = 22.5°. Errors are expressed in decibels. They increase as kr increases at least for kr ≤ 4. That is, the higher the frequency is and the larger the distance from the origin is, the larger the error will be. However, for a given kr, errors decrease as the Ambisonic order increases, or given the errors, the maximal allowable kr increases with the order of Ambisonics. For example, given the error of Err2(kr) ≤ −14 dB, Q = 1-, 2-, and 3-order reproduction have the
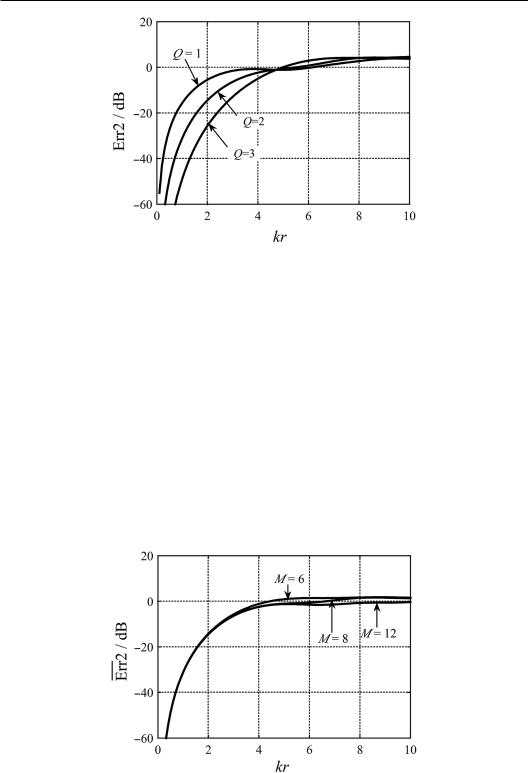
410 Spatial Sound
Figure 9.7 Mean square errors of the reconstructed sound field for Q = 1-, 2-, and 3-order horizontal Ambisonics with M = 8 secondary sources arranged at 0°, ±45°, ±90°, ±135°, and 180° and the target plane wave from θS = 22.5°.
maximal allowable kr of 1.1, 2.0, and 2.9, respectively. For a region with r = a = 0.0875 m (average head radius), the corresponding upper frequency limits are 0.7, 1.2, and 1.9 kHz. This example indicates that Ambisonics can reconstruct a target sound field within a region centered at the origin, and the radius of the region and upper frequency limit for accurate reconstruction increases with the order. This phenomenon is a basic feature of Ambisonics.
Figure 9.8 illustrates the mean square error of complex amplitude of the wavefront for Q = 2-order horizontal Ambisonics with M = 6, 8, and 12 secondary sources to explore the influence of the number of secondary sources on the error of the reconstructed sound field for a given order reproduction. For M = 6 array, which satisfies the number given in Equation (4.3.67), secondary sources are arranged in ±30°, ±90°, and ±150°. For M = 8 array, secondary sources are arranged identical to the example in Figure 9.7. For M = 12 array, secondary sources are arranged from the azimuth of 0° with a uniform azimuthal interval of 30°. For a target incident plane wave, the mean error in Equation (9.5.2) can be equivalently
Figure 9.8 Mean square error of complex amplitude of the wavefront for Q = 2-order horizontal Ambisonics with M = 6, 8, and 12 secondary sources.

Analysis of multichannel sound field recording and reconstruction 411
calculated on the basis of the mean error in a fixed receiver position over a variation in the incident plane wave direction −180° < θS ≤ 180°. The results are illustrated in Figure 9.8. For kr ≤ 2 that does not exceed the limit given by Shannon–Nyquist spatial sampling theorem in Equation (9.3.15), errors in different numbers of secondary sources are almost identical. They increase as kr increases, but they are still less than −14 dB. For kr > 2, they are obvious; for kr = 4, they reach 0 dB. When kr > 3, errors depend on the number M of secondary sources. Moreover, they reduce slightly or at least do not increase when M increases from 6 to 8. They further reduce when M increases from 8 to 12.
Below the limit of kr < Q of Shannon–Nyquist spatial sampling theorem, Ambisonics can theoretically reconstruct a target sound field with slight errors. If the number of secondary sources is larger than the lower limit of M = (2Q + 1), errors are basically independent from the number of secondary sources. Above the limit of Shannon–Nyquist spatial sampling theorem, i.e., for kr > Q, the error of the reconstructed sound field increases obviously. Errors generally depend on the order and number of secondary sources and target source (or plane wave) directions because the reconstructed sound field is the coherent superposition of those caused by multiple secondary sources. In the above case, increasing the number of secondary sources slightly reduces the error in the reconstructed sound field for Q > kr. In other cases, increasing the number of secondary sources may increase the error. The analysis of binaural pressures in Section 12.1.3 yields similar results.
Solvang (2008) analyzed the relationship between spectral distortion (SD) in a reconstructed plane wave and the number of secondary sources in horizontal Ambisonics, where M ≥ (2Q + 1) secondary sources are arranged uniformly in a circle for Q-order reproduction. The conclusion for kr < Q is similar to that observed in Figure 9.8, i.e., the SD in the reconstructed sound pressure is small and basically independent of the number of secondary sources. SD is obvious for kr > Q. In this case, further increasing the number of secondary sources to M > (2Q + 1) increases SD. However, using M > (2Q + 1) secondary sources reduces the SD around the region of kr = Q. Therefore, Solvang concluded that the number of secondary sources should be chosen as a compromise of the SD at kr > Q and around kr = Q. Solvang’s conclusion is different from the observation in Figure 9.8 at kr > Q and around the region of kr = Q.
However, Solvang used a mean SD over receiver positions as the error criterion. SD is defined as the ratio between the power spectra of the reconstructed sound pressure and the target sound pressure. A deviation of SD from a unit (0 dB) indicates an error in reconstructed sound pressures. When the mean SD over receiver positions is calculated, errors in different receiver positions may be wiped out. For example, if the SDs at two receiver positions are 1.5 and 0.5, respectively, the mean SD is a unit (0 dB), which is obviously inappropriate. Therefore, the mean SD in Solvang’s analysis is low, and the conclusion should be revised. By contrast, the mean square complex amplitude error of wavefront in Equation (9.5.2) is used for the calculation in Figure 9.8, and the problem is avoided.
The aforementioned error analysis can be extended to spatial reproduction. For P(r, Ω, f) and P′(r, Ω, f), Equation (9.5.2) can be extended to the integral overall a spherical surface with radius r:
Err2 |
kr |
|
|
P r, , f P(r, , f ) |
|
2d |
. |
(9.5.4) |
||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
P r, , f |
|
2d |
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
For a target incident plane wave with unit amplitude, the integral in the denominator of Equation (9.5.4) is 4π.
