122 |
8 Horns and Stepped Ducts |
The reactive (imaginary) component, j ω x, is the so-called co-vibrating medium mass. This component swings about without transporting active power. The active (real) component, c, becomes relatively (not absolutely!) stronger with increasing distance. For x λ/2π, Z f approaches c. Note that c is the field-impedance in a tube with a constant diameter and, thus, the specific field-impedance of the medium, Z w.
8.3 Exponential Horns
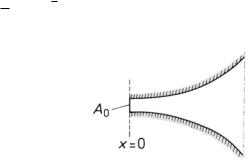
The area function of the exponential horn—see Fig. 8.5—is given by
A(x) = A0 e2 x , |
(8.19) |
with > 0 being the so-called flare coefficient. Now differentiation deliveres
1 d A |
|
d [ln A(x)] |
|
2 |
and, thus, |
(8.20) |
||||||
|
|
|
|
|
|
|
||||||
A(x) dx |
= |
|
|
= |
||||||||
dx |
|
|
|
|
|
|
|
|||||
|
|
|
∂2 p |
+ 2 |
∂ p |
= |
1 ∂2 p |
(8.21) |
||||
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
∂ x2 |
∂ x |
c2 |
|
∂t2 |
|||||
The structure of this equation is easily understood by applying complex notation, which leads to
∂2 p |
∂ p |
+ |
ω2 |
|
|||||||
|
|
+ 2 |
|
|
|
|
p |
= 0 , |
(8.22) |
||
|
|
||||||||||
∂ x2 |
∂ |
x |
c2 |
||||||||
|
|
|
|||||||||
an equation which recalls the equation of the damped oscillator—see Sect. 2.3.
We confine to the forward progressing wave again and, consequently, try the approach p(x) = e γ x . This trial leads to the characteristic quadratic equation
Fig. 8.5 Cross-section of an exponential horn
8.3 Exponential Horns |
123 |
|
|
|
|
|
γ |
2 + |
2 |
γ |
+ |
ω2 |
= 0 |
|
|
|
|
|
|
(8.23) |
|||||
with its two solutions |
c2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
γ 1, 2 |
|
2 |
|
|
ω2 |
|
|
|
j |
ω2 |
|
2 . |
(8.24) |
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
= − ± |
− |
|
|
= − ± |
|
|
|
− |
|
|
|
|||||||||
|
|
c |
|
|
c |
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||
The complex quantity, γ, is termed propagation coefficient, whereby |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
γ = α + j β , |
|
|
|
|
|
|
(8.25) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where α is the damping coefficient and β the phase coefficient.
Hence, the solution of the wave equation is an exponential function decreasing with x. This kind of decreasing is called spatial damping. The general solutions for
p and v in the forward-progressing wave results as |
|
|||||||||||||||
|
|
|
|
→(0) e− x e−j ( |
|
|
) x = |
p |
→(0) eαx e−jβ x , and |
|
||||||
|
p |
→(x) = |
p |
ω2 |
− 2 |
(8.26) |
||||||||||
|
c2 |
|||||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
+ j |
|
|
|
|
|
|
|||||
|
|
|
|
|
c2 |
− 2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
v →(x) = |
|
|
|
|
|
|
|
p |
→(x) . |
(8.27) |
||
|
|
|
|
|
|
j ω |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Again, the solution for v has been derived from the one for p by applying Euler’s equation (8.1).
A prerequisite for wave propagation is that the expression under the square root is positive and, thus, results in a phase coefficient, β. This is the case when ω2/c2 > 2 and, accordingly, 2π/λ > holds. The condition is fulfilled above a limiting angular
frequency |
|
ωl = c . |
(8.28) |
Below ωl , there is an exponential fade-out as the expression under the root becomes negative, and we end up with pure damping without wave propagation. This condition means physically that mass is shifted about, but no energy is transported because no sufficient compression takes place. ωl decreases with decreasing flare coefficient, . In other words, the slimmer the horn, the lower the limiting frequency.
Note that the phase speed, c ph, in the exponential horn, is different from that in a
free plane wave, c, viz, |
ω |
|
|
|
|
ω |
|
|
|
|
|
c ph = |
= |
|
|
|
|
|
. |
(8.29) |
|||
|
|
|
|
|
|
|
|
||||
β |
|
|
|
|
|
|
|||||
|
|
ω |
|
2 |
|
|
|||||
|
|
|
c |
|
− 2 |
|
|||||
124 |
8 Horns and Stepped Ducts |
Furthermore, c ph is frequency-dependent. This effect is called dispersion since different frequency components travel with different speed and, thus, the different wave components arrive at the end of the horn at different instances.2
The so-called group-delay distortions, which describe the frequency-dependent delay of the envelope of a transmitted signal, are highest close to the limiting frequency. The group delay, τ gr , over a wave-traveling distance of l is in our case
|
|
|
|
|
|
|
|
|
dβ |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
τ gr = |
|
= |
|
|
|
|
|
|
, |
|
|
|
|
|
|
(8.30) |
||||
|
|
|
|
|
|
dω |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
ω |
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c 1 − |
ωl |
|
|
|
|
|
|
|
|
|
||||
The field-impedance in the exponential horn, Z f , is given by |
|
|
|
|
||||||||||||||||||||||
|
|
|
p |
|
|
j ω |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
Z f |
|
|
→ |
|
|
|
|
|
1 |
|
ωl |
|
2 |
|
j |
|
ωl |
(8.31) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= v |
= |
|
|
|
|
= |
− ω |
|
|
+ |
|
ω |
||||||||||||||
|
ω2 |
|
|
|
||||||||||||||||||||||
|
→ |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
+ j c2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
As with the conical horn, Z f |
approaches c = Zw |
with increasing frequency |
||||||||||||||||||||||||
because of Z f |
c for ω ωl. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8.4 Radiation Impedances and Sound Radiation
The acoustic power that is sent out by an electro-acoustic transducer or any other sound source is proportional to the real part of the impedance, r rad = Re{Z rad}, that terminates the source at its acoustic output port. Since this impedance is formed by coupling the sound field with the source, we call it radiation impedance, Z rad, and its real part radiation resistance, r rad. The radiation impedance is a mechanic impedance—refer to Sect. 4.5—namely,
|
|
|
|
Z rad = |
F |
|
|
(8.32) |
|
|
|
|
|
|
. |
|
|
||
|
|
|
|
v |
|
|
|||
The radiated power, then, is |
|
|
|
|
|
|
|
||
|
|
|
1 |
Re { Z rad} | v |2 = |
1 |
r rad | v |2 . |
|
||
|
P = |
(8.33) |
|||||||
|
|
|
|||||||
|
2 |
2 |
|||||||
The following relation holds between the field-impedance, Z f , and the radiation impedance, Z rad,
Z rad = Z f d A , (8.34)
A
2 This fact contributes to the characteristic sound of horn loudspeakers.
8.4 Radiation Impedances and Sound Radiation |
125 |
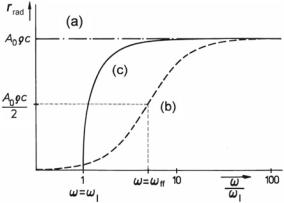
Fig. 8.6 Schematic plot of the radiation resistance. Frequencies normalized to the limiting frequency, ωl, of the exponential horn (a) Tube with constant cross-section. (b) Conical horn. (c) Exponential horn
with A being the effective radiation area.
For transducers that radiate into a horn, the effective area is equal to the area of the horn’s mouth in the optimal case. In the synopsis shown in Fig. 8.6, we assume that the tube/horn is so long that no waveforms are reflected from the opening, but that the diameter is still small compared to the wavelength, namely, d λ. This is an idealizing assumption of course.
In summing up, we get for the tube with a constant cross-section, |
|
||||||||||||||||||||
|
|
r rad = Zw A0 = c A0 , |
|
|
|
|
|
|
|
|
|
(8.35) |
|||||||||
for the conical horn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ω |
x0)2 |
|
|
|
|
|
||||
r rad ( A0) = A0 |
Re{ Z f } = A0 |
c |
|
|
|
c |
|
|
|
|
, |
(8.36) |
|||||||||
1 |
+ |
( |
ω |
x |
)2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c |
0 |
|
|
|
|
|
|||
and for the exponential horn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r rad ( A0) |
|
A0 |
Re |
|
Z f |
|
A0 |
c |
|
1 |
|
|
|
ωl |
|
2 . |
(8.37) |
||||
= |
{ |
} = |
− |
|
ω |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
For the conical horn, ω ff , which forms the near-field/far-field division at a given distance from the mouth, x1, is independent of the opening angle of the horn. For the exponential horn, however, the limiting angular frequency, ωl depends on the flare coefficient, .
The exponential horn, among all horns that Webster’s equation covers, is the one with the steepest increase of Re{ Z rad} = r rad as a function of frequency. However,