13. Определение деформационных характеристик в одноосных испытаниях. Закон Гука. Коэффициент Пуассона.

Рассмотрим простой опыт на одноосное сжатие образца изотропного грунта (рис. 3.1). В этом опыте образец грунта в форме параллелепипеда с размерами hbb сжимается по вертикальной оси Oz напряжением _z  ₁. В результате деформируется на величину s вдоль оси Oz и расширяется на b в перпендикулярной к Oz плоскости.

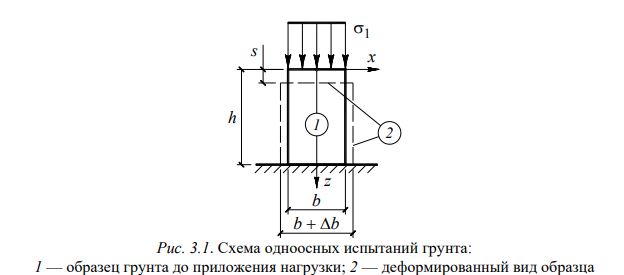
По результатам испытаний строят график зависимости относительной осевой деформации _z  ₁  s/h от осевых напряжений ₁. Здесь можно выделить два основных участка. При ₁ < _cr график по своему очертанию довольно близок к линейному, затем, при ₁ > _cr, линия приобретает существенно нелинейный характер, пока не становится практически параллельной оси O₁ и, в конце концов, в некоторой точке B при ₁  R_c произойдет разрушение образца. Поведение грунта при разрушении будет подробно рассмотрено ниже.

Участок ОА обладает малой кривизной и для практических целей вполне достаточно, если применить к нему линейную аппроксимацию, т.е. принять зависимость между деформациями и напряжениями линейной. Следовательно, при ₁ < _cr для описания поведения грунта справедлив закон Гука: 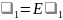, где E – модуль деформации грунта, Мпа.

Из этих же испытаний легко найти коэффициент Пуассона, который по определению равен отношению поперечной относительной деформации ₃ к продольной ₁: .

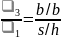14. Компрессионные испытания. Схема опыта. Диаграмма сжатия. Определение модуля деформации по диаграмме сжатия.

Компрессия – это сжатие грунта без бокового расширения. Компрессионные испытания проводятся в специальных приборах-одометрах, или компрессионных приборах.

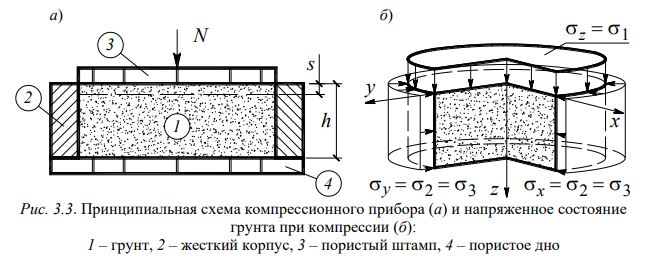
Образец грунта 1 при испытании помещается в жесткую недеформируемую цилиндрическую обойму 2 и в ней обжимается вертикальной нагрузкой N, передаваемой через верхний штамп 3. Наличие отверстий в верхнем штампе 3 и в дне 4 обеспечивает отток воды из образца при его сжатии. Для снижения сил трения грунта о стенки обоймы принимается определенное соотношение высоты и диаметра образца. Обычно высота образца h  25 мм, а его площадь A  60 см².

По результатам испытаний для каждой ступени вычисляют относительную деформацию ₁  s/h и строят график зависимости ₁  f(₁). Такой график, приведенный на рис. 3.4 а, называют диаграммой сжатия. В случае линейного (или близкой к линейному) характера графика ₁  f(₁) для интерпретации результатов компрессионных испытаний можно использовать закон Гука. Тогда искомыми деформационными характеристиками будут постоянные (модуль деформации E и коэффициент Пуассона ).

С целью определения модуля деформации запишем обобщенный закон Гука для компрессионных условий: ,

,

.

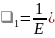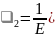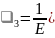Поскольку при компрессии ₂  ₃, выразим ₃ через ₁ с помощью, например, второго уравнения: , .

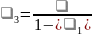Введем понятие коэффициента бокового давления .

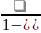Тогда соотношение между ₁ и ₃ примет вид: ₃  ₁ .

Данное выражение представляет собой обобщенный закон Гука для компрессионных условий и, одновременно, уравнение диаграммы сжатия при компрессии. От линейного (одноосного) закона Гука его отличает множитель в скобках, который, по существу, является коэффициентом, учитывающим невозможность бокового расширения:

Переходя к интервалам напряжений, запишем выражение для модуля деформации из уравнения диаграммы сжатия: