Постановка плоской задачи теории предельного равновесия грунтов (тпрг). Понятие о линиях скольжения.
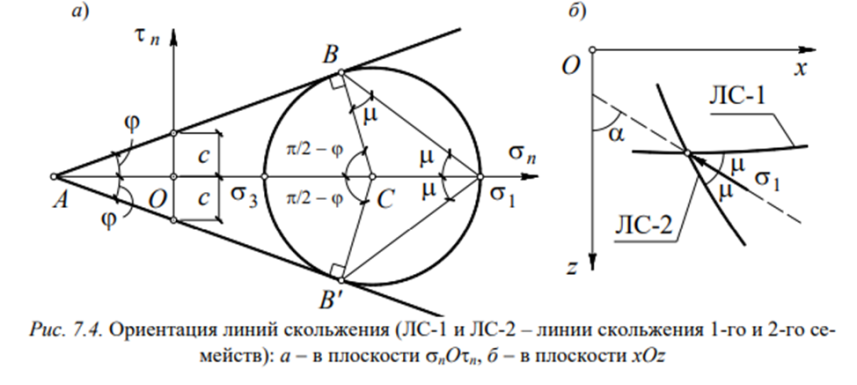
Цель решений теории предельного равновесия грунтов (ТПРГ) – построение поля предельных напряжений в основании и определение его несущей способности. Базовой моделью грунта в ТПРГ является жестко-пластическая модель грунта, основанная на законе Кулона-Мора (см. п. 1.7). В основе построения статических решений ТПР лежат две гипотезы. 1. Основание находится в равновесии. 2. В каждой точке основания грунт находится в предельно напряженном состоянии. Другими словами, в каждой точке грунта напряжения находятся на поверхности текучести Кулона-Мора.
Формализация этих гипотез сразу приводит к замкнутой системе дифференциальных уравнений: гипотеза 1 записывается в виде двух уравнений равновесия с тремя неизвестными функциями напряжений x, z , xz, а гипотезу 2 выражает закон Кулона-Мора (1.5), где фигурируют те же три напряжения.
Поверхность скольжения – это поверхность, по которой происходит сдвиг массы грунта (например, оползневого тела) относительно неподвижной части грунтового массива. Этот процесс имеет место в результате общей потери устойчивости массива, исчерпания его несущей способности. Под линией скольжения будем понимать след поверхности скольжения на расчетной плоскости чертежа. Понятие линии скольжения особенно удобно для решения задач в условиях плоской деформации.
Несущая способность оснований. Формула Терцаги. Решения для невесомого сыпучего основания, идеально-связного основания и весомого сыпучего основания.
Формула Терцаги. В практических расчетах определение несущей способности оснований фундаментов чаще всего сводится к вычислению предельного давления или ее равнодействующей по трехчленной формуле Терцаги. Эта формула имеет фундаментальное значение в механике грунтов, а с ее помощью могут быть описаны результаты решений весьма широкого круга задач о предельном давлении.
Решения для невесомого сыпучего основания, идеально-связного основания и весомого сыпучего основания.
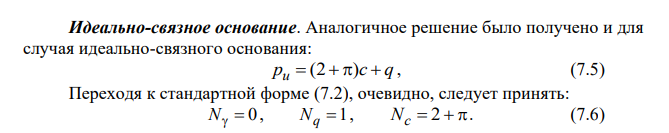
Предельная высота вертикального откоса. Равноустойчивые контуры склонов.
Предельная высота вертикального откоса. Рассмотрение проблемы устойчивости откосов и склонов начнем с наиболее простой задачи определения предельной высоты вертикального откоса. Этот вопрос имеет значение, как в теоретическом, так и в практическом отношении. Известно, что грунт в состоянии держать весьма крутые и даже вертикальные откосы. Однако также понятно, что высота такого откоса ограничена она зависит от прочности грунта и внешнего давления на бровке откоса. Рассмотрим схему, показанную на рис. 7.6. Грунт характеризуется параметрами прочности и c, удельным весом . Предположим также, что на бровке действует нагрузка интенсивностью p. Предельную высоту вертикального откоса обозначим через hu. При z > hu прочности грунта оказывается недостаточно, чтобы сохранять вертикальное очертание склона, и намечается тенденция к его выполаживанию. Следовательно, на глубине hu откос находится в предельно напряженном состоянии.
Для идеально-сыпучего грунта (c 0) имеем hu 0, что является очевидным фактом, поскольку несвязанные друг с другом песчаные частицы в принципе не в состоянии держать вертикальный откос.
