37. Задача Буссинеска. Напряжения, эпюры, осадка поверхности.

38. Задача о произвольной нагрузке на горизонтальном основании (пространственная задача).

39. Задача Лява-Короткина. Напряжения, эпюры. Коэффициент рассеивания напряжений.

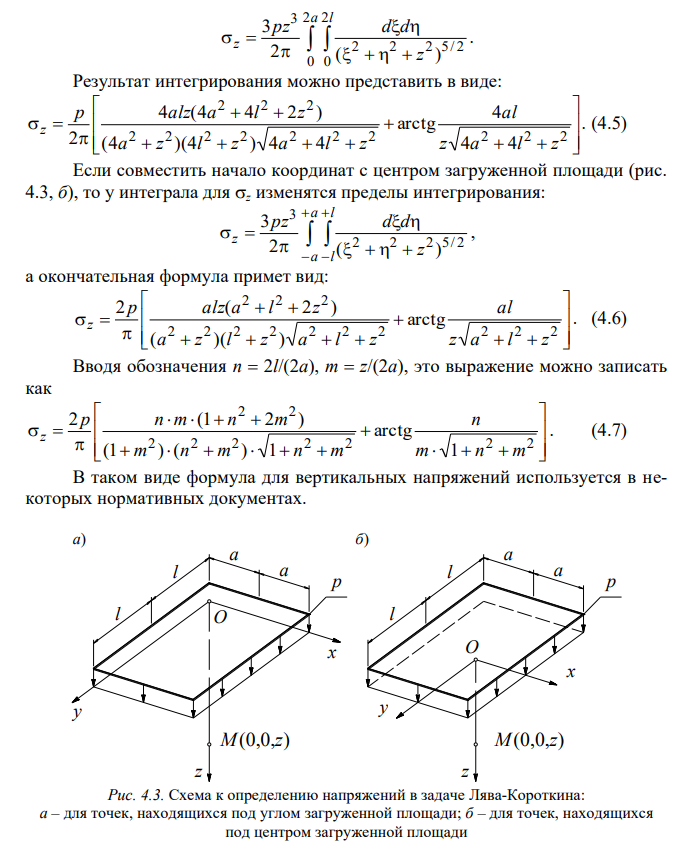
Пусть по прямоугольной в плане площадке размером 2a * 2l действует равномерное нормальное давление p. Центр декартовой системы координат поместим в один из углов загруженной площадки (рис. 4.3, а). Определим вертикальные напряжения в точке M, расположенной на оси Oz.

Пользуясь приемом, изложенным выше, в соответствии с формулой (4.4) запишем выражение для вертикального напряжения 6_z в точке M с координатами x=0, y=0, z:

Коэффициент рассеивания напряжений. Для формул (4.6)…(4.7) часто используют следующую компактную запись:

Коэффициент зависит от размеров загруженной площади и от координат точки, в которой определяются напряжения. Его значения изменяются в пределах от единицы на границе основания, т.е. непосредственно под нагрузкой, и до нуля при бесконечном удалении от места приложения нагрузки.

40. Задача Лява-Короткина. Метод угловых точек. Формула Шлейхера.

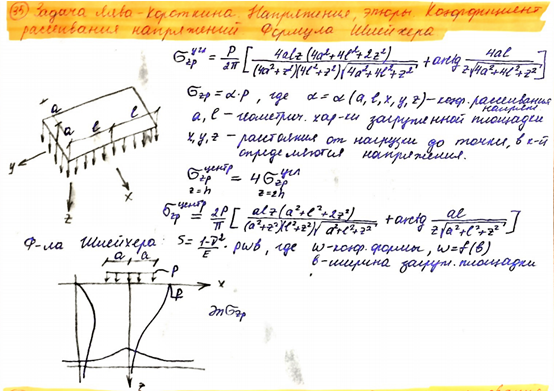
Допустим, что равномерно распределенная нагрузка p действует на горизонтальной поверхности основания в границах прямоугольной площади 1-2-3-4. Требуется определить напряжения в точке M, расположенной на некоторой глубине z под загруженной площадью (рис. 4.4, а)

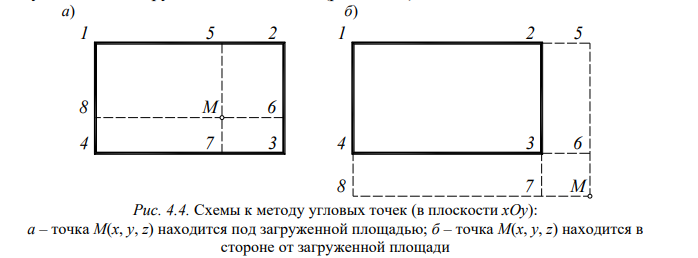
Проведем в плоскости xOy, т.е. на поверхности основания, через проекцию точки M два отрезка, параллельных сторонам загруженного прямоугольника. В результате точка M окажется под углами загруженных прямоугольников 1-5-M-8, 5-2-6-M, M-6-3-7 и 8-M-7-4. Соответственно, воспользовавшись формулой (4.5) можно вычислить напряжений в точке M от каждого из указанных прямоугольников, а результат, пользуясь принципом суперпозиции, сложить:

Предположим теперь, что точка M находится на вертикали, проходящей в стороне от загруженной площади 1-2-3-4 (рис. 4.4, б). В уровне поверхности основания (плоскость xOy) достроим до проекции точки M прямоугольник 1-5-M-8. Вычислим напряжения _z^1-5-M-8 , возникающие в точке M, от нагрузки p, которая действовала бы по всей площади 1-5-M-8. Но, поскольку фактически давление действует только на участке 1-2-3-4, то из напряжения z 1-5-M-8 необходимо вычесть напряжения, возникающие от прямоугольников 4-6-M-8 и 2-5-M-7: соответственно, _z^4-6-M-8 и _z^2-5-M-7 . Однако, площади 4-6-M-8 и 2-5-M-7 имеют пересечение, образующее прямоугольник 3-6-M7, а это значит, что он дважды участвовал в процедуре «вычитания». Следовательно, к полученному результату необходимо прибавить напряжения, возникающие в точке M от давления p по площади 3-6-M-7. Окончательно имеем:

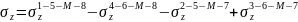
Перемещения и формула Шлейхера. Пользуясь выражением для вертикального перемещения w задачи Буссинеска (4.2) и принятой схемой интегрирования (см. рис. 4.2), запишем формулу для величины w в точках под углом загруженного прямоугольника (см. рис. 4.3, а):

Для точек, находящихся под центром загруженной площади, в двойных интегралах для w следует поменять пределы интегрирования с 0…2a и 0…2l соответственно на –a…a и –l…l. Если нагрузка распределена по площади другой формы, то выражения для A и B соответствующим образом изменятся. Кроме того, выражение (4.10) можно использовать в рамках метода угловых точек.

Положив в (4.10) z  0, получим формулу для расчета осадки поверхности в задаче Лява-Короткина. Обозначим ширину фундамента b  2a и перепишем равенство (4.10) в виде:

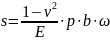
где   коэффициент формы, зависящий от формы площади нагружения.

Выражение называется формулой Шлейхера. Её используют для расчета модуля деформации грунта в штамповых испытаниях. Также можно применять для определения осадок однородного основания.