More Complex Filters—Adding Zeros

Lowpass and Highpass Filter Characteristics  177

of roll-off, but always the response stays rolled-off; it does not come back up again. There are no deep notches in the amplitude response; once the roll-off is established, it just keeps on going down. However, filters with notches in their stopband that plunge to the infinite depths (in theory, at least) have their uses, and their study makes up a large proportion of filter theory.

When a faster roll-off than Butterworth is required, without the passband amplitude ripples of the

Chebyshev, one possibility is the Inverse Chebyshev, which adds a notch in the response just outside the passband. Notches have slopes that get steeper and steeper as you approach the actual notch frequency, so the roll-off is much accelerated.

Elliptical (Cauer) filters permit ripple in the passband and have notches in the response just outside the passband, and offer even steeper roll-off slopes. They are also very economical on hardware. Suppose you need a serious lowpass filter that must roll-off from −0.5 dB to −66 dB in a single octave (not very likely in crossover design, but stay with me). This would need a 13th-order Butterworth filter

or an 8th-order Chebyshev, but a 5th-order Cauer filter can do the job with much greater economy in components and also in power, because fewer amplifiers are required.

In filter design the notch frequencies are known as “zeros” because they are the frequencies at which the complex equations describing the filter response give a value of zero—in other words, infinite attenuation. Real filters do not have infinitely deep notches, as the depth usually depends on component tolerances and amplifier gain-bandwidths.An exception is the Bainter filter, which gives beautifully deep notches without tweaking; more on the Bainter later.

The design procedures for these filters are not at all straightforward, and I am simply going to show some design examples. These can have their component values scaled in the usual away to obtain different cutoff frequencies.

It is of course always possible to add notches to a filter response by, for example, cascading a Butterworth filter with a notch filter placed suitably in the stopband. This is however not as efficient as Inverse Chebyshev or Cauer filters (though it is conceptually much simpler), because in the latter the notch is properly integrated with the filter response, and so better passband flatness and sharper rolloffs are obtained.

Inverse Chebyshev Filters (Chebyshev Type II)

The Inverse Chebyshev filter, also known as the Chebyshev Type II filter, does not have amplitude ripples in the passband; instead it has notches (zeros) in the stopband. Like the Chebyshev filter, it is directed towards getting a faster roll-off than a Butterworth filter while meeting other conditions; it offers a maximally flat passband, a moderate group delay, and an equi-ripple stopband. The cutoff

frequency is usually defined to be at the −3 dB level, though other definitions can be used. The Inverse Chebyshev filter uses zeros, so it is not an all-pole filter. These filters are complicated to design, and it would not be a good use of space to try and plod through the procedures here. Instead I am presenting a finished design which can be easily scaled for different frequencies.

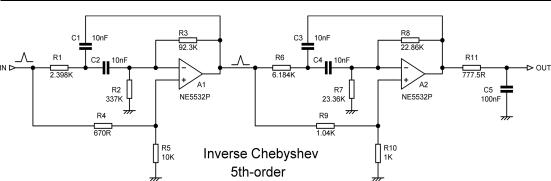
Figure 7.34 shows a simple 5th-order Inverse Chebyshev filter with a cutoff frequency of 1 kHz. It is made up of two lowpass notch filters followed by a 1st-order lowpass filter. The most familiar

178  Lowpass and Highpass Filter Characteristics

Figure 7.34: A 5th-order Inverse Chebyshev lowpass filter made up of two lowpass notch filters followed by a 1st-order lowpass. Cutoff frequency 1 kHz.

notch filter is the symmetrical sort, where the gains on either side of the notch are the same; there are however also lowpass notch filters where, as the frequency increases, the response dives down into the notch but comes up again to level out at a lower gain, and highpass notch filters where the gain is lower on the low-frequency side of the notch. There is more on this in Chapter 12 on bandpass and notch filters.

Here the two lowpass notch filters are of the Deliyannis-Friend type, [12][13] which consists basically of a multiple-feedback (MFB) lowpass filter with an extra signal path via the non-inverting input that generates the notch by cancellation. It is not exactly obvious, but these filter stages are non-inverting in the passband. The notch depth is critically dependent on the accuracy of the ratio set by R4, R5.

The complete filter has an overall gain in the passband of +1.3 dB. The filter structure is based on an example given by Van Valkenburg. [14]

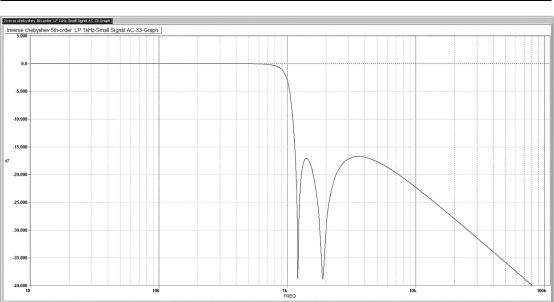
The amplitude response in Figure 7.35 shows how the first notch in the stopband, at 1.22 kHz, is very narrow and makes the roll-off very steep indeed. However, the response naturally also starts to come back up rapidly, but this is suppressed by the second notch (at 1.88 kHz), which has a lower Q and is therefore broader and buys time, so to speak, for the final 1st-order filter to start bringing in a useful amount of attenuation. Each time the response comes back up it reaches −17 dB; this is what is meant by an equi-ripple stopband. Variations on this type of filter with non-equal stopband ripples may not be officially Inverse Chebyshev filters, but they can be useful in specific cases.

To scale this circuit for different frequencies you can alter the capacitors, keeping C1 = C2 and

C3 = C4 and the ratios of C1, C3 and C5 the same, or you can change resistors R1, R2, R3 and R6, R7,

R8 and R11, keeping all their ratios the same. You can of course change both capacitors and resistors to get appropriate circuit impedances. R4 and R5 can be altered, but their ratio must remain the same, and likewise with R9 and R10; remember that the accuracy of this ratio controls notch depth. R11 and

C5 can be altered as you wish, quite separately from any other alterations to the circuit, so long as its time-constant is unchanged.

More details on the design of Inverse Chebyshev filters can be found in Van Valkenburg. [15]

Lowpass and Highpass Filter Characteristics  179

Figure 7.35: The amplitude response of a 5th-order Inverse Chebyshev lowpass filter. Note how the passband is maximally flat (no ripples) before the very steep roll-off. Cutoff frequency 1 kHz.

Elliptical Filters (Cauer Filters)

Elliptical filters (also called Cauer filters) are basically a combination of Chebyshev and Inverse Chebyshev filters; amplitude ripples in the passband are accepted as the price of a faster roll-off, and there are also one or notches (zeros) in the stopband to steepen the roll-off rate. They have a sharp cutoff, high group delay, and greatest stopband attenuation. They are sometimes called complete-

Chebyshev filters or Zolotarev filters.

As for the Chebyshev filter, the definition of an elliptic filter cutoff frequency depends on the passband ripple amplitude. In most filter design software any value of attenuation can be defined as the cutoff point.

The design of elliptical filters is not simple, and even the authors of filter textbooks that are a morass of foot-long complex equations are inclined to say things like “it is rather involved . . .” and recommend you use published tables to derive component values. Regrettably, the use of these tables is in itself rather hard going, so here I am just going to give one example of how these filters are put together.

This can be easily scaled for different frequencies. There is another example in Chapter 12 on notch crossovers.

The amount of passband ripple in an elliptic filter is sometimes quoted as a “reflection coefficient” percentage ρ, which as you might imagine is a hangover from transmission line theory, and not in my opinion a very helpful way of putting it.

Lowpass and Highpass Filter Characteristics  181

Figure 7.37: The amplitude response of the 3rd-order elliptical lowpass filter. The lower trace is the final output, and the upper trace is the signal from the first stage. Cutoff frequency 1 kHz.

C5, the final response is the 3rd-order lower trace in Figure 7.37. The 0.2 dB ripple in the passband is just visible.You will observe that as the frequency increases, once the drama of the notch is over the ultimate roll-off slope is only 6 dB/octave because the lowpass notch response is now flat, and so only the final 1st-order filter is contributing to the roll-off. This is the price you pay for implementing a fast roll-off with a filter that is only 3rd-order. Fourth-order filters that have an ultimate roll-off slope of 12 dB/octave are described in Chapter 5 on notch crossovers.

To scale this circuit for different frequencies you can alter all the capacitors, keeping their ratios to each other the same, or the resistors R1–4 and R7.You can of course change both to get appropriate circuit impedances. R5 and R6 can be altered, but their ratio must remain the same.

We have compared the roll-off of the previous filters by looking at the attenuation at 10 kHz, a decade above the 1 kHz cutoff frequency. That is less helpful here because of the way the amplitude response comes back up at high frequencies; the response at 10 kHz is −42 dB, but in my simulation the attenuation at the bottom of the notch (at 2.6 kHz) was about−65 dB. The passband gain is +12.7 dB because of the positive feedback applied to the notch network, and in many cases this will be less than convenient. Elliptical filters can sometimes be very useful for crossover use, for if we have an otherwise good drive unit with some nasty behaviour just outside its intended frequency range, the notch can be dropped right on top of it.

This elliptical filter and the Inverse Chebyshev filter are the only ones in this chapter that are not allpole filters. More details on the design of elliptical filters can be found in Williams and Taylor [18] and Van Valkenburg. [19]