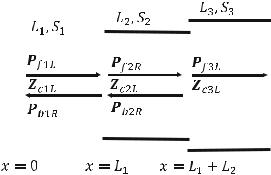
11.7Numerical Method for Molding of Pipelines

Objective

Numerical methods can be used to calculate power transmission coefficients of pipelines. A pipeline is constructed with three pipes as shown below. Acoustic waves enter the left-hand side of the pipeline and exit the right-hand side:

Given:

Pipe 1: L1 ¼ 0.1 [m],S1 ¼ 0.5 [m2]

Pipe 2: L2 ¼ 0.1 [m],S2 ¼ 0.5 [m2]

Pipe 3: L3 ¼ 0.1 [m],S3 ¼ 0.5 [m2]

P f 3L ¼ 1; Pb3L ¼ 0

At 1000 Hz, calculate:

(a)The complex acoustic impedance Zc1L of the combined wave at the LHS of Pipe 1

(b)The complex amplitude of pressure of both the forward wave (Pf1L) and backward wave (Pb1L) at the LHS of Pipe 1

(c)The power transmission coefficient Tw

Hint: Doing this example by hand can be difficult because the complex acoustic impedances are complex numbers. We will use the three MATLAB functions provided in the MATLAB program section (Sect. 11.8) for this example. The same results can be obtained with any suitable programming languages

Solution

The method is demonstrated using three functions described in the Computer Program Section (Sect. 11.8). The following is the logic for this numerical method:

acoustic impedance (Zc2L) of the combined wave at the LHS of Pipe 2. The input and output arguments of the function are as follows:

Input Arguments:

Zc2L: Complex acoustic impedance of the combined wave at the LHS of Pipe 2 L1: Length of Pipe 1

S1: Cross-section area of Pipe 1

Zc2L: Complex acoustic impedance of the combined wave at the LHS of Pipe 2 k: Wavenumber

LoC: Characteristic impedance

Output Arguments:

Zc1L: Complex acoustic impedance of the combined wave at the LHS of Pipe 1

Formulas:

This function is based on Formula 5 as:

Function 2: TRANSFER_PRESSURE

The function TRANSFER_PRESSURE calculates the complex amplitude of pressure of both the forward wave (Pf1L) and backward wave (Pb1L) at the LHS of Pipe 1 based on the acoustic impedance at the LHS of Pipe 2. The input and output arguments of the function are as follows:

Input Arguments:

Pc2L: Complex amplitude of pressure of the combined wave at the LHS of Pipe 2

L1: Length of Pipe 1

S1: Cross-section area of Pipe 1

Zc2L: Complex acoustic impedance of the combined wave at the LHS of Pipe 2 k: Wavenumber

LoC: Characteristic impedance

Output Arguments:

Pf1L: Complex amplitude of pressure of the forward wave at the LHS of Pipe 1

Pb1L: Complex amplitude of pressure of the backward wave at the LHS of Pipe 1

Formulas:

This function is based on the two formulas below, which are the combined results of Formulas 2A–2B and 4A–4B as shown in Example 11.2:

Function 3: Power Transmission Coefficient Input arguments:

Pi: Complex amplitude of the pressure of the forward (incident) wave in the inlet pipe

Po: Complex amplitude of the pressure of the forward (outward) wave in the outlet pipe

Pr: Complex amplitude of the pressure of the backward (reflected) wave in the inlet pipe

Zi: acoustic impedance (real number) of the forward (incident) wave in the inlet pipe

Zo: the acoustic impedance of the forward (outward) wave in the outlet pipe

Zr: the acoustic impedance of the backward (reflected) wave in the inlet pipe

Output arguments:

Rw: Power reflection coefficient

Tw: Power transmission coefficient

Formulas:

MATLAB Code (Function)

function [Pf1L,Pb1L]=TransferPressure_fb1Lfb2L(Zf1,Zf2,Pf2L,Pb2L, L1,k)

%Purpose: Transfer comoplex pressure from Pipe 2 to Pipe 1

%Input variables:

%Zf1: acoustic impedance of forward wave of Pipe 1

%Zf2: acoustic impedance of forward wave of Pipe 2

%Pf2L: forward pressure at LHS of Pipe 2

%Pb2L: backward pressure at LHS of Pipe 2

%L1: length of Pipe 1

%k: wave number

%Output variable:

%Pf1L: forward pressrue at LHS of Pipe 1

%Pb1L: backward pressrue at LHS of Pipe 1

%Formula 4A’-B’ + 2A-B

%Pf1L=0.5*((1+Zf1/Zf2)*Pf2L + (1-Zf1/Zf2)*Pb2L)*exp( j*k*L1);

%Pb1L=0.5*((1-Zf1/Zf2)*Pf2L + (1+Zf1/Zf2)*Pb2L)*exp(-j*k*L1);

%Formula 4A’-B’ + 2A-B

[Pf1R,Pb1R]=TransferPressure_fb1Rfb2L(Zf1,Zf2,Pf2L,Pb2L); [Pf1L,Pb1L]=TransferPressure_fb1Lfb1R(Pf1R,Pb1R,L1,k); end

function [Pf1R,Pb1R]=TransferPressure_fb1Rfb2L(Zf1,Zf2,Pf2L,Pb2L)

%Purpose: Transfer comoplex pressure from Pipe 2 to Pipe 1

%Input variables:

%Zf1: acoustic impedance of forward wave of Pipe 1

%Zf2: acoustic impedance of forward wave of Pipe 2

%Pf2L: forward pressure at LHS of Pipe 2

%Pb2L: backward pressure at LHS of Pipe 2

%Output variable:

%Pf1R: forward pressrue at RHS of Pipe 1

%Pb1R: backward pressrue at RHS of Pipe 1

%Formula 4A’-B’

Pf1R=0.5*((1+Zf1/Zf2)*Pf2L + (1-Zf1/Zf2)*Pb2L);

Pb1R=0.5*((1-Zf1/Zf2)*Pf2L + (1+Zf1/Zf2)*Pb2L); end

function [Pf1L,Pb1L]=TransferPressure_fb1Lfb1R(Pf1R,Pb1R,L1,k)

%Purpose: Transfer comoplex pressure from RHS to LHS of Pipe 1

%Input variables:

%Pf1R: forward pressure at RHS of Pipe 1

%Pb1R: backward pressure at RHS of Pipe 1

%L1: length of Pipe 1

%k: wave number

%Output variable:

%Pf1L: forward pressrue at LHS of Pipe 1

%Pb1L: backward pressrue at LHS of Pipe 1

%Formula 2A-B

Pf1L=Pf1R*exp( j*k*L1); Pb1L=Pb1R*exp(-j*k*L1); end

function [Pf1R,Pb1R]=TransferPressure_fb1Rfb1L(Pf1L,Pb1L,L1,k)

%Purpose: Transfer comoplex pressure from LHS to RHS of Pipe 1

%Input variables:

%Pf1L: forward pressrue at LHS of Pipe 1

%Pb1L: backward pressrue at LHS of Pipe 1

%L1: length of Pipe 1

%k: wave number

%Output variable:

%Pf1R: forward pressure at RHS of Pipe 1

%Pb1R: backward pressure at RHS of Pipe 1

%Formula 2C-D

Pf1R=Pf1L*exp(-j*k*L1); Pb1R=Pb1L*exp( j*k*L1); end

function [Pf1R,Pb1R]=TransferPressure_fb1Rfb2R(Zf1,Zf2,Pf2R,Pb2R, L2,k)

%Purpose: Transfer comoplex pressure from Pipe 2 to Pipe 1

%Note: This function does not work for Pipe 2 is the end pipe

%Input variables:

%Zf1: acoustic impedance of forward wave of Pipe 1

%Zf2: acoustic impedance of forward wave of Pipe 2

%Pf2R: forward pressure at RHS of Pipe 2

%Pb2R: backward pressure at RHS of Pipe 2

%L2: length of Pipe 2

%k: wave number

%Output variable:

%Pf1R: forward pressrue at RHS of Pipe 1

%Pb1R: backward pressrue at RHS of Pipe 1

%Formula 2A-B + 4A’-B’

%Pf1R=0.5*((1+Zf1/Zf2)*Pf2R*exp(j*k*L2)+...

%(1-Zf1/Zf2)*Pb2R*exp(-j*k*L2));

%Pb1R=0.5*((1-Zf1/Zf2)*Pf2R*exp(j*k*L2)+

%(1+Zf1/Zf2)*Pb2R*exp(-j*k*L2));

%Formula 2A-B + 4A’-B’

[Pf2L,Pb2L]=TransferPressure_fb1Lfb1R(Pf2R,Pb2R,L2,k); [Pf1R,Pb1R]=TransferPressure_fb1Rfb2L(Zf1,Zf2,Pf2L,Pb2L); end function[Pf1R,Pb1R]=TransferPressure_EndPipe(Zf1,Zf2,Pf2L)

%Purpose: Transfer comoplex pressure from Pipe 2 (end pipe) to Pipe 1

%Input variables:

%Zf1: acoustic impedance of forward wave of Pipe 1

%Zf2: acoustic impedance of forward wave of Pipe 2 (The end pipe)

%Pf2L: forward pressure at LHS of Pipe 2 (Pb2L=0) (The end pipe)

%Output variable:

%Pf1R: forward pressrue at RHS of Pipe 1

%Pb1R: backward pressrue at RHS of Pipe 1

%Formula 2A-B (with Pb2L=0)

Pf1R=0.5*(1+Zf1/Zf2)*Pf2L;

Pb1R=0.5*(1-Zf1/Zf2)*Pf2L;

End

function[Pf1R,Pb1R]=TransferPressure_fb1Rc2L(Zf1,Zc2L,Pc2L)

%Purpose: Transfer comoplex pressure from Pipe 2 to Pipe 1

%Input variables:

%Zf1: acoustic impedance of forward wave of Pipe 1

%Zc2L: acoustic impedance of forward wave of Pipe 2

%Pc2L: combined pressure at LHS of Pipe 2

%Output variable:

%Pf1R: forward pressrue at RHS of Pipe 1

%Pb1R: backward pressrue at RHS of Pipe 1

%Formula 4A-B

Pf1R=0.5*(1+Zf1/Zc2L)*Pc2L;

Pb1R=0.5*(1-Zf1/Zc2L)*Pc2L; end

function [Zc1L]=TransferImpedance(Zf1,Zc2L,L1,k)

%Purpose: Transfer acoustic impedacne from Pike 2 to Pipe 1

%Input variables:

%Zf1: complex acoustic impedance of forward pressure of Pipe 1

%Zc1L: complex acoustic impedance of combine pressure at LHS of Pipe 1

%L1: length of Pipe 1

%k: wave number

%Output variable:

%Zc2L: complex acoustic impedance of combine pressure at LHS of Pipe 2

%Formula 5 Zc1L=Zf1*(Zc2L+j*Zf1*tan(k*L1))/(j*Zc2L*tan(k*L1)+Zf1); end

function [Tw]=get_Tw_PipeLine(P_in,Z_in,P_out,Z_out)

%calculate the Power Transmission Coeffient Tw

%P_in: Complex pressure inward

%P_out: Complex pressure outward

%Z_in: Complex acoustic impedance inward

%Z_out: Complex acoustic impedance outward

%Formula 6B

Tw=real(P_out)*real(P_out/Z_out)/(real(P_in)*real(P_in/Z_in)); end

MATLAB Code (Main Code)

function ANC_PRJ051_FilterAndResonator_D191116B clear all % remove all variables

clf % remove all figures %-------------------------------------------------

--------------------%

% Section 1: Define Variables and Parameters %---------------------------------------------------

------------------%

%define the parameter of the wave function

%define the air properties

c=340; % [m/s] loC=415; % [Rayl]

%define the dimensions of the pipe line iCase=3;

if iCase==1 % Test Case (Horn Shaped Pipeline)

%sPipe=[0.002; 0.004; 0.006; 0.008]; % area [m^2]

%lPipe=[0.025; 0.025; 0.025; 0.025]; % length [m] sPipe=[0.2; 0.6; 0.9; 1.2]; % area [m^2] lPipe=[0.025; 0.025; 0.025; 0.025]; % length [m] elseif iCase==2 % Low-Pass Filter

sPipe=[0.002; 0.008; 0.002]; % area [m^2] lPipe=[0.025; 0.015; 0.025]; % length [m] elseif iCase==3 % Band Stop Filter

%sPipe=[0.002; 0.00001]; % area [m^2]

%lPipe=[0.05; 0.00001]; % length [m] sPipe=[0.002; 0.004; 0.00001]; % area [m^2] lPipe=[0.01; 0.04; 0.00001]; % length [m] elseif iCase==4 % High-Pass Filter sPipe=[0.001; 0.10]; % area [m^2] lPipe=[0.020; 0.015]; % length [m]

end

%define the dimensions of the main pipe SiMain=0.002; % m2 % area of the main line inlet pipe SoMain=0.002; % m2 % area of the main line outlet pipe

%define the frequency sweep

nFreq=8192;

df=0.5; % [Hz]

freq=[0:1:nFreq-1]*df; % 0:0.5:4095.5 [Hz] %---------------------------------------------------------

------------%

% Section 2: Setup %---------------------------------------------------------

------------%

% define the dimensions Tw=zeros(nFreq,1);

nPipe=max(size(lPipe)); % Number of pipes in pipe line side branch ZiPipe=zeros(nPipe,1); % Incident Impedance of the pipe line side branch

ZcPipe=zeros(nPipe,1); % combined Impedance of the pipe line side branch

for iPipe=1:1:nPipe ZiPipe(iPipe)=loC/sPipe(iPipe); end

%---------------------------------------------------------

------------%

% Section 3: Calculation %---------------------------------------------------------

------------%

% calculate Tw for each frequency for iw=1:1:nFreq k=2*pi*freq(iw)/c;

%define the dimensions of the matrices PfR=zeros(nPipe,1); % forward pressure at the right end PbR=zeros(nPipe,1); % backward pressure at the right end

%pressure for the nth pipe (the left one) PfR(nPipe)=1.0; % the pon is given PbR(nPipe)=0.0;

%calculate the combined impedance for the nth pipe (the left one) ZcPipe(nPipe)=ZiPipe(nPipe); % the last pipe (has no return wave)

%get PfR and PbR of pipe n-1

[PfR_iPipe_temp,PbR_iPipe_temp]=TransferPressure_EndPipe(...

ZiPipe(nPipe-1),ZiPipe(nPipe),PfR(nPipe)); PfR(nPipe-1)=PfR_iPipe_temp; PbR(nPipe-1)=PbR_iPipe_temp;

% transfer Zc from (nPipe) to (nPipe-1) ZcPipe(nPipe-1)=TransferImpedance(ZiPipe(nPipe-1),ZcPipe(nPipe), lPipe(nPipe-1),k);

%transfer Zc from (nPipe-1) to (iPipe=1) for iPipe=nPipe-2:-1:1

%pressure for the iPipe pipe

[PfR_temp,PbR_temp]=TransferPressure_fb1Rfb2R(ZiPipe(iPipe), ZiPipe(iPipe+1),PfR(iPipe+1),PbR(iPipe+1),lPipe(iPipe+1),k); PfR(iPipe)=PfR_temp;

PbR(iPipe)=PbR_temp;

% transfer Zc from (iPipe+1) to (iPipe) ZcPipe(iPipe)=TransferImpedance(ZiPipe(iPipe),ZcPipe(iPipe+1), lPipe(iPipe),k);

end

% calculate Tw for Low-Pass filternPipe=size(PfR,1); PfR_PfR1=PfR/PfR(1); % make the input pressure 'REAL' by making it 1 Tw(iw,1)=get_Tw_PipeLine(PfR_PfR1(1),ZiPipe(1),PfR_PfR1(nPipe),