Файловый архив студентов. Файловый архив студентов.
1304 вуза, 5161 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Башкирский Государственный Аграрный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
акустика / lin_h_bengisu_t_mourelatos_zp_lecture_notes_on_acoustics_and.pdf
Скачиваний:
152
Добавлен:
04.05.2023
Размер:
12.68 Mб
Скачать
☆
►Содержание►

11.2

Complex Acoustic Impedance

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

283

P

c2L

 

1

 

 

1

 

P

f 2L and

Pc2L e

jkL2

e

jkL2

 

P

 

 

 

e

jkL2

e

jkL2

 

1

 

 

f 2R

Pc2R

¼

 

 

 

 

 

 

Pb2L

 

 

 

 

 

Pc2R

¼

 

 

1

 

Pb2R

 

Inverse the 2x2 matrix to get:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

 

 

 

1

 

 

 

 

 

jkL2

1

 

P

 

 

 

 

 

 

 

 

 

 

P f 2L

¼

 

 

 

 

 

e

 

Pc2L

 

 

 

 

 

 

 

 

ejkL2

e

 

jkL2

e

jkL2

 

 

 

 

 

 

 

 

 

b2L

 

 

 

 

 

 

 

 

 

 

 

1

 

c2R

 

 

 

 

 

 

 

 

 

 

P f 2R

 

 

 

 

 

 

1

 

 

1

 

e jkL2

 

Pc2L

 

 

 

 

 

 

 

 

 

P

 

¼

 

 

 

 

 

ejkL2

P

 

 

 

 

 

 

 

 

 

b2R

ejkL2

e jkL2

 

 

1

c2R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Proof of Formula 2G

Based on Formulas 1E and 1A–1B, Uc2L ¼ Uf2L + Ub2L ¼ (Pf2L Pb2L)/Zf2 and Uc2R ¼ Uf2R + Ub2R ¼ (Pf2R Pb2R)/Zf2, and using Formula 2A–2B gets:

 

Uc2L

=

1

 

 

 

 

2ejkL2

e jkL2

 

P f 2R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

Pb2R

 

 

 

 

 

 

 

 

 

 

 

 

Uc2R

Z f 2

 

 

1

 

 

 

 

 

e jkL2

P

 

 

 

 

¼ Z1f 2

 

 

e jkL2

1 e jkL2

 

1

 

 

 

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e jkL2

e

 

jkL2

 

1

 

 

e jkL2

Pc2L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c2R

 

 

 

 

1

 

 

 

 

 

 

1e

 

e

jkL2

þ e

jkL2

 

 

2

 

 

 

P

 

 

 

 

 

¼

 

 

 

 

 

 

 

 

 

 

 

 

 

Pc2L

 

 

 

 

Z f 2

 

e jkL2

jkL2

 

 

 

 

 

e

jkL2

 

jkL2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

þ e

 

 

c2R

 

 

 

Using Euler’s formula, the equation above arrives at:

Uc2R

¼ Z f 2sinðkL2Þ

1

Þ

cosðkL2Þ

Pc2R

Uc2L

 

j

cosðkL2

 

1

Pc2L

Proof of Formulas 2B and 2D

(Homework Exercise 11.1 Part a)

11.2Complex Acoustic Impedance

Formulas 3A–3B

284

11 Power Transmission in Pipelines

Pipe 2

,

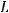
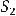
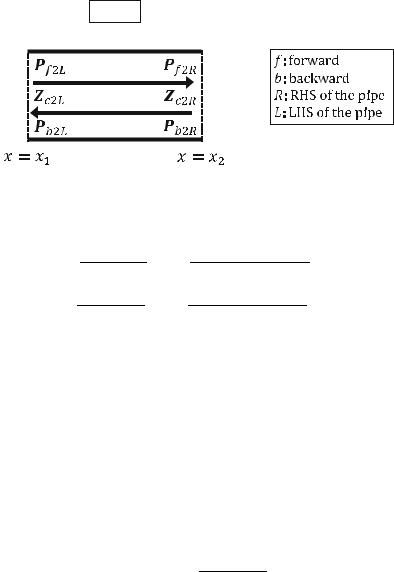
The acoustic impedance Zc2L at LHS of Pipe 2 is related to the acoustic impedance Zf2 as shown in Formula 3A. The acoustic impedance Zc2R at RHS of Pipe 2 is related to the acoustic impedance Zf2 as shown in Formula 3B:

Z

c2L ¼

Z

P f 2L þ Pb2L

¼

Z

 

 

f 2 P f 2L

 

Pb2L

 

 

 

 

 

 

 

 

Z

c2R ¼

Z

P f 2R þ Pb2R

¼

Z

 

 

f 2 P f 2R

 

Pb2R

 

 

 

 

 

 

 

 

where Z f 2 ¼

ρoc

is a real number.

 

S2

 

 

 

P f 2RejkL2

þ Pb2Re jkL2

Formula 3A

Þ

 

 

P f 2RejkL2

Pb2Re jkL2

f 2

 

ð

 

f 2

P f 2Le jkL2

þ Pb2LejkL2

ð

Formula 3B

Þ

P f 2Le jkL2

Pb2LejkL2

 

Proof of Formula 3B

In Pipe 2 as shown in the figure above, the pressure pf2(x, t) of a forward wave and the pressure pb2(x, t) of a backward wave are formulated in terms of complex amplitudes of the pressures Pf2L and Pb2L at LHS of Pipe 2 (x ¼ x1) as:

p f 2ðx, tÞ ¼

1

nP f 2Le jkðx x1Þejωt þ cco

 

 

 

2

 

 

 

pb2ðx, tÞ ¼

1

nPb2Lejkðx x1Þejωt þ cco

 

 

 

 

2

 

 

 

Based on Formula 3B, the acoustic impedance Zc2R at the RHS of Pipe 2 is:

 

Z

c2R

¼

Z

P f 2R þ Pb2R

ð

Formula 3B

Þ

 

 

f 2 P f 2R

 

Pb2R

 

 

 

 

 

 

 

 

 

 

 

 

 

Based on Formulas 2C and 2D, the pressures Pf2R and Pb2R at RHS of Pipe 2 are related to the pressures Pf2L and Pb2L at LHS of Pipe 2 as:

P f 2R ¼ P f 2Le jkL2

ðFormula 2CÞ

11.3Balancing Pressure and Conservation of Mass

Pb2R ¼ Pb2LejkL2

Substituting Formulas 2C and 2D to Formula 3B yields:

Z

c2R ¼

Z

 

P f 2R þ Pb2R

¼

Z

P f 2Le jkL2

þ Pb2LejkL2

 

 

f 2

P f 2R Pb2R

 

f 2

P f 2Le jkL2

Pb2LejkL2

where:

Z f 2 ¼ ρoc

S2

Proof of Formula 3A

(Homework Exercise 11.1 Part b)

285

ðFormula 2DÞ

ðFormula 3BÞ

11.3Balancing Pressure and Conservation of Mass

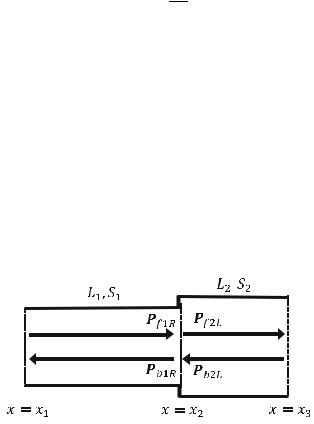
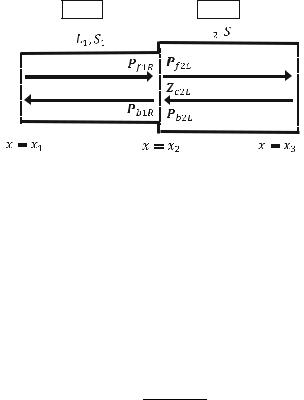
The cross-sectional areas of Pipe 1 and Pipe 2 are S1 and S2, respectively, as shown in the figure below. The pressures of the forward wave and the backward wave in Pipe 1 at RHS of Pipe 1 (x ¼ x2) are Pf1R and Pb1R, respectively. The pressures of the forward wave and backward wave in Pipe 2 at LHS of Pipe 2 (x ¼ x2) are Pf2L and Pb2L, respectively:

Pipe 1

 

Pipe 2

 

 

 

 

,

The following conditions must be satisfied at the intersection between the two pipes:

I.All pressures are balanced at the intersection according to Newton’s third law of motion:

P f 1R þ Pb1R =P f 2L þ Pb2L

ðstate of equilibriumÞ
Pipe 1

286

11 Power Transmission in Pipelines

II.The volume flow rate (U = VS) inward is equal to the volume flow rate outward according the conservation of mass, assuming that the air has a constant density:

U f 1R þ Ub1R ¼ U f 2L þ Ub2L

ðconservation of massÞ

11.4Transformation of Pressures

Formulas 4A–4D

The cross-sectional areas of Pipe 1 and Pipe 2 are S1 and S2, respectively, as shown in the figure below. The pressures of the forward wave and the backward wave in Pipe 1 at RHS of Pipe 1 (x ¼ x2) are Pf1R and Pb1R, respectively. The pressures of the forward wave and the backward wave in Pipe 2 at LHS of Pipe 2 (x ¼ x2) are Pf2L and Pb2L, respectively:

Pipe 2

,

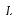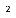
The pressures Pf1R and Pb1R (RHS of Pipe 1) can be formulated in terms of the

pressures Pf2L and Pb2L (LHS in Pipe 2) as:

 

 

 

 

 

 

 

 

 

 

 

1

 

Z f 1

 

 

 

 

 

 

 

1

 

 

 

 

 

Z f 1

 

 

 

 

P f 1R ¼

 

 

1 þ

 

 

 

 

 

P f 2L þ

 

 

 

1

 

 

 

 

 

Pb2L

ðFormula 4A’Þ

2

Z f 2

2

Z f 2

Pb1R ¼

1

1

Z f 1

 

P f 2L þ

1

 

1

þ

Z f 1

Pb2L

ðFormula 4B’Þ

2

Z f 2

 

 

2

 

Z f 2

 

 

 

 

 

1

1 þ

Z f 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P f 1R ¼

 

 

 

 

 

Pc2L

 

 

 

 

 

 

ðFormula 4AÞ

 

 

 

2

Zc2L

 

 

 

 

 

 

 

 

 

 

 

 

Pb1R ¼

1

1

Z f 1

 

 

 

 

 

 

 

 

 

 

 

 

Pc2L

ðFormula 4BÞ

 

 

 

 

 

2

Zc2L

 

 

 

 

 

 

 

 

 

 

Pb1R

 

 

 

 

 

 

Zc2L Z f 1

 

 

 

Formula 4C

 

 

 

 

 

 

 

 

 

 

 

P f 1R

¼

 

 

 

 

ð

Þ

 

 

 

 

 

 

 

 

 

 

 

 

Zc2L

þ

Z f 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Pc2L

 

¼

 

 

 

 

 

2Zc2L

 

ðFormula 4DÞ

 

 

 

 

 

 

 

 

 

 

P f 1R

 

 

 

Zc2L

þ

Z f 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11.4 Transformation of Pressures

287

where:

 

 

 

 

 

 

 

Pc2L ¼ P f 2L þ Pb2L

ðFormula 1DÞ

Z

Z

P f 2L þ Pb2L

ð

Formula 3A

Þ

c2L ¼

 

f 2 P f 2L

 

Pb2L

 

 

 

 

 

 

 

 

Z f 2 ¼ ρoc

S2

Proof of Formulas 4A–4D

Based on Newton’s third law of motion (state of equilibrium) and conservation of mass:

P f 1R þ Pb1R =P f 2L þ Pb2L

ðstate of equilibriumÞ

ð1Þ

U f 1R þ Ub1R =U f 2L þ U f 2L

ðconservation of massÞ

ð2Þ

Based on Formulas 1A and 1B, changing the volume flow rate U to P/Z and changing Zb1 and Zb2 to 2Zf1 and 2Zf2, respectively, yield:

 

P f 1R

 

Pb1R

 

P f 2L

 

 

 

Pb2L

 

 

 

þ

 

 

=

 

 

 

 

 

þ

 

 

 

 

 

Z f 1

Zb1

Z f 2

Zb2

!

P f 1R

2

Pb1R

=

P f 2L

2

Pb2L

Z f 1

Z f 1

 

Z f 2

Z f 2

 

! P f 1R 2Pb1R =

Z f 1

 

P f 2L Pb2L

Z f 2

 

Solve Pf1R and Pb1R from Eq.(1) and Eq.(3) to get:

P f 1R ¼ 2

1 þ Z f 2

P f 2L þ 2

1 Z f 2

Pb2L

1

 

Z f 1

1

 

Z f 1

 

Pb1R ¼ 2

1 Z f 2

P f 2L þ 2

1 þ Z f 2

Pb2L

1

 

Z f 1

1

 

 

Z f 1

 

ð3Þ

ðFormula 4A’Þ

ðFormula 4B’Þ

Based

on

Formula

1D, Pc2L ¼ Pf2L

+

Pb2L,

and

3A, Zc2L

¼ Z f 2

 

P f 2L þPb2L

, rearrange Eq.(3) to get:

 

 

 

 

 

 

P f 2L Pb2L

 

 

 

 

 

 

 

!

 

 

 

Z f 1

 

 

 

þ

 

 

 

 

 

 

Z f 2

 

P f 2L þPb2L

 

 

 

 

 

 

P f 1R 2Pb1R =

 

P f 2L Pb2L

 

P f 2L

 

Pb2L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

! P f 1R 2Pb1R =

Z f 1

Pc2L

 

 

 

 

 

 

 

 

 

Zc2L

 

 

 

 

Solve Pf1R and Pb1R from Eq.(1) and Eq.(4) to get:

on Formula,

ð4Þ

Соседние файлы в папке акустика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности