Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5171 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Башкирский Государственный Аграрный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
акустика / lin_h_bengisu_t_mourelatos_zp_lecture_notes_on_acoustics_and.pdf
Скачиваний:
153
Добавлен:
04.05.2023
Размер:
12.68 Mб
Скачать
☆
►Содержание►

9.3 Octave Bands

237

Example 9.4: Solution

(a)The RMS pressure can be formulated in the frequency domain using Parseval’s theorem as:

1 p2RMS ¼ P2o þ 12 X P2k

k¼1

The RMS pressure can be calculated in the frequency domain by substituting the given frequency contents Pk into the equation above:

pRMS2 ¼ Po2

þ

1

1

Pk2

=

P2

=

32

hðPaÞ2i

2

k¼1

21

2

 

 

 

X

 

 

 

 

 

 

(b) The unweighted SPL calculated in the frequency domain is:

 

 

3

! ½dB&

 

 

Lp ¼ 20 log 10

PRMS

p2

Pr

¼ 20 log 10 20

10 6

Note that both RMS pressure and unweighted SPL calculated in the frequency domain (this example) are the same as if calculated in the time domain (the previous example). This is the expected result because of Parseval’s theorem.

9.3Octave Bands

Octave bands are commonly used in the fields of acoustics and vibration. Two major benefits of using octave bands are as follows: (1) it provides insight of power distribution vs. frequency, and (2) it allows to apply weight to the different frequencies.

9.3.1Center Frequencies and Upper and Lower Bounds of Octave Bands

Spectra obtained by Fourier transform (FT) using frequency in linear scale are called the narrow band spectra. However, such detail in spectral resolution is not always needed. Hence, spectra can be obtained in wider frequency bands for easier analysis. The most commonly used frequency bands are octave bands (frequency in logarithmic scale). Each octave band has a center frequency and a band width, defined as:

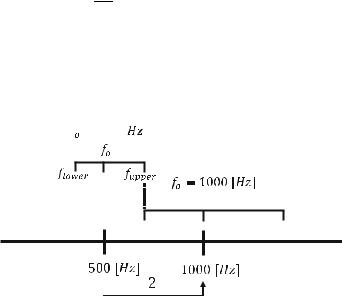
238

9 Sound Pressure Levels and Octave Bands

 

k

½octave&

f o ¼ 1000 2

1

½octave&

~

½center frequency&

½Hz&; k ¼ 54;

f lower ¼

f o

¼ f o ∙ 2

1

;

½lower limit frequency&

 

p2

 

2

 

f upper ¼

 

 

o ¼

 

o ∙

 

1

 

½

 

1

&

 

f

22

;

 

 

p2 f

 

 

 

 

upper limit frequency

 

 

 

 

f upper ¼ f lower ∙ 2

 

 

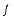= 500 [ ]

 

center

lower

upper

The center frequencies and lower and upper limit frequencies of octave bands are:

1 Octave

 

 

 

 

 

 

 

 

 

Band

 

Center (Quoted)

 

Center (Quoted)

Center (Calculated)

Lower (Limit)

 

Upper (Limit)

 

[-]

 

 

 

[Hz]

[Hz]

[Hz]

[Hz]

 

 

 

 

 

fo

fo*2^(-1/2)

 

fo*2^(1/2)

 

0

 

1000*2^(-5)

 

31.50

31.25

22.10

 

44.19

 

1

 

1000*2^(-4)

 

63.00

62.50

44.19

 

88.39

 

2

 

1000*2^(-3)

 

125.00

125.00

88.39

 

176.78

 

 

 

 

 

 

 

176.78

 

353.55

 

3

 

1000*2^(-2)

 

250.00

250.00

 

 

 

 

 

 

 

 

353.55

 

707.11

 

4

 

1000*2^(-1)

 

500.00

500.00

 

 

5

 

1000*2^0

 

1000.00

1000.00

707.11

 

1414.21

 

 

 

 

 

 

 

1414.21

 

2828.43

 

6

 

1000*2^1

 

2000.00

2000.00

 

 

7

 

1000*2^2

 

4000.00

4000.00

2828.43

 

5656.85

 

 

 

 

 

 

 

5656.85

 

11313.71

 

8

 

1000*2^3

 

8000.00

8000.00

 

 

9

 

1000*2^4

 

16000.00

16000.00

11313.71

 

22627.42

 

9.3 Octave Bands

239

9.3.2Lower and Upper Bounds of Octave Band and 1/3 Octave Band

There are other popular wide bands in the analysis that can use 13 octave bands, 101 octave bands, and 121 octave bands. The formula for 13 octave bands is shown below:

 

k

½octave&

f o ¼ 1000 2

3

½octave&

~

½center frequency&

½Hz&; k ¼ 1913;

 

 

f o

 

 

¼ f o ∙ 2

1

f lower ¼

 

 

 

6

;

 

p2

1=3

f upper ¼

 

 

1=3

f o ¼ f o ∙

1

p2

 

26

 

 

 

 

 

1

 

 

f upper ¼ f lower ∙ 23

 

 

In general, m-octave bands can be generated using the relationships below:

f o ¼ 1000 ∙ ð2mÞk, where m ¼ 1, 12 , 13 , 14

f lower ¼ 2 m=2 f o; f upper ¼ 2m=2 f o; f upper ¼ 2m f lower

Example 9.6

Given the time domain function p(t) with frequency contents Pk as below:

pðtÞ ¼ X4k¼1Pk cos ð2π f kt þ θkÞ

where:

f k ¼ 250 k ½Hz&

And the magnitudes and phases are:

P1 = 0.023[Pa];

θ1

= 0 [deg]

P2 = 0.127[Pa];

θ2

= 270[deg]

P3 = 0.127[Pa];

θ3

= 270[deg]

P4 = 0.283[Pa];

θ3

= 270[deg]

Determine the combined sound pressure level (SPL) using the following three methods:

240

9 Sound Pressure Levels and Octave Bands

(a)Calculate the combined SPL from the summation of the square of the RMS pressures.

(b)Calculate the combined SPL from the SPL spectrum of all the existing frequencies.

(c)Calculate the combined SPL from the SPL spectrum of the octave bands.

Example 9.6: Solution

(a)Calculate the combined SPL from the summation of the square of the RMS pressures.

The RMS pressures of each frequency are:

2

 

=

P12

 

 

 

0:0232

 

 

2

 

pRMS,250Hz

 

 

¼

 

 

 

 

 

 

 

Pa

 

2

2

2

2

 

 

 

p2

= p2

 

 

Hz

=

P2

 

 

0:127

 

Pa2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

¼

 

 

 

 

 

 

RMS,500Hz

RMS,750 2

 

 

 

2

2

2

 

 

2

 

=

 

P4

 

 

 

0:283

 

 

 

 

2

 

pRMS,1000Hz

 

 

 

¼

 

 

 

 

 

 

Pa

 

 

2

 

 

 

 

2

 

 

 

The combined SPL from the summation of the square of the RMS pressure is:

 

 

 

 

 

 

 

 

 

 

¼

 

 

 

 

 

 

 

Pr2

 

!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Lp

 

 

10 log 10

 

RMS,total

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

:

0232

 

0

:

1272

 

0

1272

 

0:

2832

 

 

 

 

 

 

 

 

 

 

 

0

 

 

þ

 

 

 

 

þ

 

 

:

 

 

þ

 

 

 

1

 

 

 

 

 

 

¼

10 log

10

 

 

2

 

 

 

2

 

 

 

 

2

 

 

2

 

 

dB

& ¼

81:495

½

dB

&

 

 

B

 

 

 

 

 

 

20 10 6

 

 

 

 

 

 

C½

 

 

 

 

 

 

@

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

 

 

 

 

 

 

(b)Calculate the combined SPL from the SPL spectrum of all the existing frequencies:

 

¼

 

 

Pr2

!

¼

 

 

 

20 10 6 2!½ & ¼

½ &

 

 

 

P2

 

 

 

 

 

 

 

 

 

0:0232

 

 

 

 

Lp,250Hz

 

10 log 10

 

RMS, 250Hz

 

 

10 log 10

 

 

2

 

 

dB

58:2037 dB

 

 

P2

!

 

 

0:1272

 

 

 

¼

 

¼

 

 

 

 

 

½ &

 

 

Pr2

 

 

 

 

20 ∙ 10 6 2!½ & ¼

Lp,500Hz

 

10 log 10

 

RMS,500Hz

 

 

 

 

10 log 10

 

 

2

 

 

dB

73:0452 dB

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

p,750Hz ¼

L

 

 

 

 

 

 

 

 

 

 

 

 

p,500Hz

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

0:2832

 

 

!½dB& ¼ 80:0048½dB&

 

 

 

 

P

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

RMS,1000Hz

 

 

 

 

 

 

 

 

 

Lp,1000Hz ¼ 10 log 10

 

 

 

! ¼ 10 log 10

 

 

20 ∙ 10 6

 

2

 

Pr2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Соседние файлы в папке акустика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности