9.2Sound Pressure Levels

9.2.1Power-Like Quantities

All power-like physical quantities can be formulated as levels or using the decibel scale.

The definition and the units of sound power w are shown below:

The sound power w can be formulated in terms of pressure, velocity, and area:

hJ i

w ¼ PRMSVRMSS s

For plane waves moving at speed c, because VRMS ¼ PρRMS, we arrive at:

oc

The following are some power-like physical quantities that can be formulated as levels:

• Sound power level (SWL):

• Peak-to-peak velocity square:

• Peak-to-peak acceleration square:

Remarks

• Sound pressure level is a power-like quantity because W ¼ Re ðPÞ Re ðUÞS ¼

Re ðPÞ Re PZ , where Z is the acoustic impedance that relates pressure P and velocity U.

•Only (1) sound pressure level and (2) sound power level have well-established reference values, but there is no established international reference for other power-like physical quantities. For levels other than the sound pressure level and power level, their reference values must be provided for calculating their associated power-like quantities.

•The definition of levels and the decibel scale requires a reference value. When a power-like physical quantity is presented as a level and decibel scale, this powerlike quantity is compared to the reference value. Therefore, the benefit of using a level and decibel scale is to make comparing different physical quantities easier. For example, RMS pressure has an international reference value of 20 [μPa], and this reference value allows comparing RMS pressure using dB instead of μPa.

9.2.2Sound Power Levels and Decibel Scale

A sound power level describes the acoustic power radiated by a source with respect to the international reference wr ¼ 10 12[W ¼ Watt]:

9.2.3Sound Pressure Levels and Decibel Scale

Sound pressure is not a power-like quantity, but its squared value is proportional to sound power: w / p2. The sound pressure level in decibels (SPL in dB) is thus:

where Pr is the international reference sound pressure based on an auditory threshold of human hearing at 1000 Hz:

Pr ¼ 20 ∙ 10 6 ½Pa& ¼ 20 ½μPa& ðRMS referenceÞ

In addition, the subscript RMS of the pressure PRMS is often omitted for simplicity.

Remarks

•The number 20 before the log is the result of 10 2 where 2 is related to the power

•Sound pressure level 0 [dB] means that the sound pressure is equal to the reference pressure:

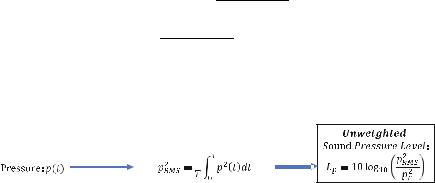
9.2.4Sound Pressure Levels Calculated in Time Domain

Example 9.4: Sound Pressure Level Calculated in Time Domain

Given:

The single-frequency pressure time domain function p(t):

pðx, tÞ ¼ P1 cos ð2π f 1tÞ

where:

P1 ¼ 3 ½Pa&

f 1 ¼ 500 ½Hz&

Calculate:

(a)The RMS pressure in the time domain

(b)The unweighted sound pressure level

Example 9.4: Solution

(a) The RMS pressure calculated in the time domain is:

or:

(b) The unweighted sound pressure level is:

or equivalently: