
- •Preface
- •Objectives of the Book
- •Style
- •Prerequisites
- •The Big Picture
- •Contents
- •1.1 Review of Complex Numbers
- •1.2 Complex Numbers in Polar Form
- •1.3 Four Equivalent Forms to Represent Harmonic Waves
- •1.4 Mathematical Identity
- •1.5 Derivation of Four Equivalent Forms
- •1.5.1 Obtain Form 2 from Form 1
- •1.5.2 Obtain Form 3 from Form 2
- •1.5.3 Obtain Form 4 from Form 3
- •1.6 Visualization and Numerical Validation of Form 1 and Form 2
- •1.8 Homework Exercises
- •1.9 References of Trigonometric Identities
- •1.9.1 Trigonometric Identities of a Single Angle
- •1.9.2 Trigonometric Identities of Two Angles
- •1.10 A MATLAB Code for Visualization of Form 1 and Form 2
- •2.2 Equation of Continuity
- •2.3 Equation of State
- •2.3.1 Energy Increase due to Work Done
- •2.3.2 Pressure due to Colliding of Gases
- •2.3.3 Derivation of Equation of State
- •2.4 Derivation of Acoustic Wave Equation
- •2.5 Formulas for the Speed of Sound
- •2.5.1 Formula Using Pressure
- •2.5.2 Formula Using Bulk Modulus
- •2.5.3 Formula Using Temperature
- •2.5.4 Formula Using Colliding Speed
- •2.6 Homework Exercises
- •3.1 Review of Partial Differential Equations
- •3.1.1 Complex Solutions of a Partial Differential Equation
- •3.1.2 Trigonometric Solutions of a Partial Differential Equation
- •3.2 Four Basic Complex Solutions
- •3.3 Four Basic Traveling Waves
- •3.4 Four Basic Standing Waves
- •3.5 Conversion Between Traveling and Standing Waves
- •3.6 Wavenumber, Angular Frequency, and Wave Speed
- •3.7 Visualization of Acoustic Waves
- •3.7.1 Plotting Traveling Wave
- •3.7.2 Plotting Standing Wave
- •3.8 Homework Exercises
- •4.2 RMS Pressure
- •4.2.1 RMS Pressure of BTW
- •4.2.2 RMS Pressure of BSW
- •4.3 Acoustic Intensity
- •4.3.1 Acoustic Intensity of BTW
- •4.3.2 Acoustic Intensity of BSW
- •4.5.1 Issues with Real Impedance
- •4.6 Computer Program
- •4.7 Homework Exercises
- •4.8 References
- •4.8.1 Derivatives of Trigonometric and Complex Exponential Functions
- •4.8.2 Trigonometric Integrals
- •5.1 Spherical Coordinate System
- •5.2 Wave Equation in Spherical Coordinate System
- •5.3 Pressure Solutions of Wave Equation in Spherical Coordinate System
- •5.4 Flow Velocity
- •5.4.1 Flow Velocity in Real Format
- •5.4.2 Flow Velocity in Complex Format
- •5.5 RMS Pressure and Acoustic Intensity
- •5.7 Homework Exercises
- •6.1 Review of Pressure and Velocity Formulas for Spherical Waves
- •6.2 Acoustic Waves from a Pulsating Sphere
- •6.3 Acoustic Waves from a Small Pulsating Sphere
- •6.4 Acoustic Waves from a Point Source
- •6.4.1 Point Sources Formulated with Source Strength
- •6.4.2 Flow Rate as Source Strength
- •6.5 Acoustic Intensity and Sound Power
- •6.6 Computer Program
- •6.7 Project
- •6.8 Objective
- •6.9 Homework Exercises
- •7.1 1D Standing Waves Between Two Walls
- •7.2 Natural Frequencies and Mode Shapes in a Pipe
- •7.3 2D Boundary Conditions Between Four Walls
- •7.3.1 2D Standing Wave Solutions of the Wave Equation
- •7.3.2 2D Nature Frequencies Between Four Walls
- •7.3.3 2D Mode Shapes Between Four Walls
- •7.4 3D Boundary Conditions of Rectangular Cavities
- •7.4.1 3D Standing Wave Solutions of the Wave Equation
- •7.4.2 3D Natural Frequencies and Mode Shapes
- •7.5 Homework Exercises
- •8.1 2D Traveling Wave Solutions
- •8.1.2 Wavenumber Vectors in 2D Traveling Wave Solutions
- •8.2 Wavenumber Vectors in Resonant Cavities
- •8.3 Traveling Waves in Resonant Cavities
- •8.4 Wavenumber Vectors in Acoustic Waveguides
- •8.5 Traveling Waves in Acoustic Waveguides
- •8.6 Homework Exercises
- •9.1 Decibel Scale
- •9.1.1 Review of Logarithm Rules
- •9.1.2 Levels and Decibel Scale
- •9.1.3 Decibel Arithmetic
- •9.2 Sound Pressure Levels
- •9.2.2 Sound Power Levels and Decibel Scale
- •9.2.3 Sound Pressure Levels and Decibel Scale
- •9.2.4 Sound Pressure Levels Calculated in Time Domain
- •9.2.5 Sound Pressure Level Calculated in Frequency Domain
- •9.3 Octave Bands
- •9.3.1 Center Frequencies and Upper and Lower Bounds of Octave Bands
- •9.3.2 Lower and Upper Bounds of Octave Band and 1/3 Octave Band
- •9.3.3 Preferred Speech Interference Level (PSIL)
- •9.4 Weighted Sound Pressure Level
- •9.4.1 Logarithm of Weighting
- •9.5 Homework Exercises
- •10.1 Sound Power, Acoustic Intensity, and Energy Density
- •10.2.2 Room Constant
- •10.2.3 Reverberation Time
- •10.3 Room Acoustics
- •10.3.1 Energy Density due to an Acoustic Source
- •10.3.2 Sound Pressure Level due to an Acoustic Source
- •10.4 Transmission Loss due to Acoustical Partitions
- •10.4.2 Transmission Loss (TL)
- •10.5 Noise Reduction due to Acoustical Partitions
- •10.5.1 Energy Density due to a Partition Wall
- •10.5.2 Sound Pressure Level due to a Partition Wall
- •10.5.3 Noise Reduction (NR)
- •10.6 Homework Exercises
- •11.1 Complex Amplitude of Pressure and Acoustic Impedance
- •11.1.3 Transfer Pressure
- •11.2 Complex Acoustic Impedance
- •11.3 Balancing Pressure and Conservation of Mass
- •11.4 Transformation of Pressures
- •11.5 Transformation of Acoustic Impedance
- •11.7 Numerical Method for Molding of Pipelines
- •11.8 Computer Program
- •11.9 Project
- •11.10 Homework Exercises
- •12.1.1 Equivalent Acoustic Impedance of a One-to-Two Pipe
- •12.2 Power Transmission of a One-to-Two Pipe
- •12.3 Low-Pass Filters
- •12.4 High-Pass Filters
- •12.5 Band-Stop Resonator
- •12.6 Numerical Method for Modeling of Pipelines with Side Branches
- •12.7 Project
- •12.8 Homework Exercises
- •Nomenclature
- •Appendices
- •Appendix 1: Discrete Fourier Transform
- •Discrete Fourier Transform
- •Fourier Series for Periodical Time Function
- •Formulas of Discrete Fourier Series
- •Appendix 2: Power Spectral Density
- •Power Spectral Density
- •Accumulated Sound Pressure Square
- •Sound Pressure Level in Each Band
- •References
- •Index
8 |
1 Complex Numbers for Harmonic Functions |
1.5Derivation of Four Equivalent Forms
1.5.1Obtain Form 2 from Form 1
Form 1 represents a simple harmonic motion using a cosine function with amplitude Ac and a sine function with amplitude As as:
xðtÞ ¼ Ac cos ðωtÞ As sin ðωtÞ |
|
|
|
|
|
|
|
|
|
|
|
|
(Form 1:RIP) |
||||||||||||||
Ac2 |
|
As2 |
2 |
Ac |
|
|
|
|
cos |
ð |
ωt |
Þ |
|
As |
|
|
sin |
ð |
ωt |
Þ |
3 |
|
|
|
|||
|
Ac |
|
|
As |
|
Ac |
|
As |
|
|
|
||||||||||||||||
¼ q |
6 |
þ |
|
|
|
þ |
|
|
7 |
|
|
|
|||||||||||||||
|
A |
þ |
|
4 |
q |
|
|
|
|
q |
|
|
|
|
5 |
|
|
|
|||||||||
|
|
A |
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
¼ Ah |
c |
cos ðωtÞ |
s |
|
sin ðωtÞi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
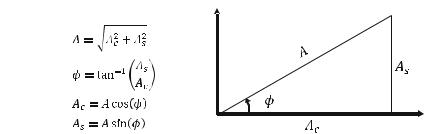
Let: |
|
|
|
|
|
|
|
|
|
|
|
|
|
A sin ðϕÞ; and ϕ ¼ tan Ac |
|||||||||||||
A Ac |
þ As |
; |
A cos ðϕÞ; |
||||||||||||||||||||||||
|
|
q |
Ac |
|
|
|
|
|
As |
|
|
|
|
|
|
|
|
|
1 As |
||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Therefore, Form 1 becomes:
xðtÞ ¼ A½ cos ðϕÞ cos ðωtÞ sin ðϕÞ sin ðωtÞ&
Geometric Relationship |
Imag |
|||||
|
|
|
|
|||
Geom 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Geom 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Geom 3 |
|
|
|
|
|
|
|
|
|
||||
Geom 4 |
|
|
|
|
|
Real |
|
|
|
|
|
|
|
Use Math 3, cos(a + b) ¼ cos (a) cos (b) sin (a) sin (b), to transfer Form 1 to Form 2 as:
x(t) ¼ A cos (ωt + ϕ) (Form 2:REP)
Note that in Form 2, A is a combined amplitude of the cosine function, and ϕ is the phase shift of the simple harmonic motion.

1.5 Derivation of Four Equivalent Forms |
9 |
1.5.2Obtain Form 3 from Form 2
Form 2 represents simple harmonic motion using one cosine function with a phase shift. Form 3 will represent the same simple harmonic motion using complex exponential functions.
Use Math 2, cos ðθÞ ¼ 12 ejθ þ e jθ as a bridge to transfer Form 2 to Form 3 as: xðtÞ ¼ 12 Ae jðωtþϕÞ þ Ae jðωtþϕÞ (Form 3:CEP)
Note that, in Form 3, the right-hand side of the equation is a real number because
the imaginary part is zero due to the addition of the complex conjugate pair, e j(ωt + ϕ) and e j(ωt + ϕ).
1.5.3Obtain Form 4 from Form 3
In Form 3, the constant phase ϕ is combined with the time variable ωt as one part of the complex exponential function, e j(ωt + ϕ). In Form 4, the constant phase ϕ will be separated from the time variable ωt to become a constant coefficient of e jωt.
Use Math 4, ea + b ¼ ea ∙ eb, to transfer Form 3 to get Form 3.5 as:
xðtÞ ¼ 21 Aejωtejϕ þ Ae jωte jϕ |
(Form 3.5) |
Note that the above form is called Form 3.5 because phase ϕ has been separated from the time variable ωt. However, e jϕ and e jϕare still not expressed in Form 4 as [Ac + jAs] and [Ac jAs].
Use Math 1, Euler’s formula, to modify Form 3.5 as:
xðtÞ ¼ 12 A½ cos ðϕÞ þ j sin ðϕÞ&ejωt þ A½ cos ðϕÞ j sin ðϕÞ&e jωt
Introducing Geom 3, Ac ¼ A cos (ϕ), and Geom 4, As ¼ A sin (ϕ), to the above equation yields:
xðtÞ ¼ 12 f½Ac þ jAs&ejωt þ ½Ac jAs&e jωtg (Form 4:CIP)
Form 4 can also be derived from Form 1 using Math 2. The derivation is straightforward and is not shown here.
