Based on the formulas shown above, topics such as cutoff frequency, echoes, and sound distortion in waveguides will be discussed in this chapter.

8.12D Traveling Wave Solutions

8.1.1Definition of Wavenumber Vectors

We have derived the relationship between the combined wavenumber k and the component wavenumbers kx and ky in Chap. 7:

k2 ¼ k2x þ k2y

Substituting the relationship between the wavenumber k and the wavelength λ:

2π k ¼ λ

into the first equation gives the relationship between the combined wavelength λ and the component wavelengths λx and λy as:

1 ¼ 1 þ 1

λ2 λ2x λ2y

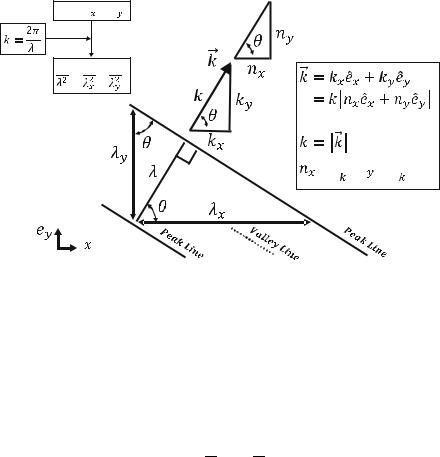
The relationship above can also be proved geometrically with trigonometric relationships:

= +

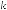
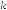
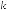
1

1 = 1 + 1

Where

= ; =

̂

̂

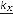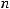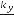
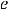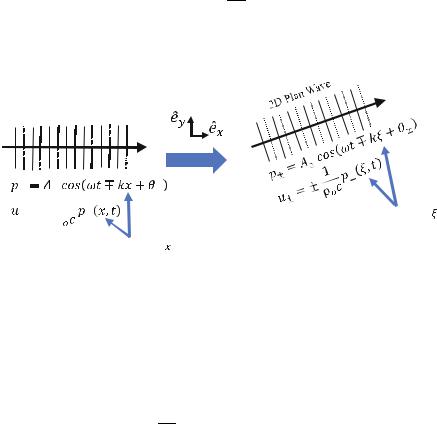
The combined wavenumber is a vector that presents the propagation direction and the magnitude of a 2D propagating plane wave as:

!

k¼ kxbex þ kybey

¼k nxbex þ nybey

where:

nx ¼ kkx ; ny ¼ kky

where bex and bey are the base vectors of the Cartesian coordinate systems and kx and ky

!

are vector components of k .

!

Note that nx and ny indicate the direction of the wavenumber vector k and have the following properties:

nx ¼ cos θ; ny ¼ sin θ

! n2x þ n2y ¼ 1

8.1.2Wavenumber Vectors in 2D Traveling Wave Solutions

The sound pressure and flow velocity of 1D plane waves were derived in Chap. 4 and are listed below for reference:

p ðx, tÞ ¼ A cos ðωt kx þ θ Þ

1

u ðx, tÞ ¼ ρoc p ðx, tÞ

The formulas above will be transferred to 2D plane waves using the wavenumber vector we learned in the previous section:

1D Plan Wave

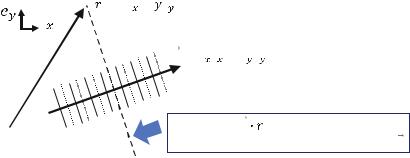
Note that the formulas of pressure and velocity on the left-hand side of the figure are for the plane wave traveling along the x-axis. The right-hand side of the figure shows the same plane wave rotated by an angle. The rotated plane wave becomes 2D and can be formulated with a new variable ξ. The formulas of pressure and velocity of the 2D plane wave are the same as the 1D plane wave except using the different variable names – x and ξ as:

p ðξ, tÞ ¼ A cos ðωt kξ þ θ Þ

1

u ðξ, tÞ ¼ ρoc p ðξ, tÞ along traveling direction

The new variable ξ is the result of the dot product of the wavenumber vector

! !

k kx, ky and the position vector r ðx, yÞ as:

!

And the velocity of the plane wave above is along the traveling direction k :

̂= ̂+ ̂

̂

̂̂

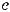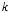
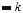
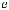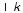
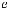The value of 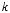is the same on a plane that is perpendicular to the wavenumber vector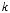

Based on the formulas above, the pressure and velocity of a 2D plane wave can be formulated in the Cartesian coordinate as:

! ’

The 2D flow velocity u of the 2D plane wave can be derived using Euler s force equation as the following:

Replacing ω and k with c yields the final form: