
- •Preface
- •Objectives of the Book
- •Style
- •Prerequisites
- •The Big Picture
- •Contents
- •1.1 Review of Complex Numbers
- •1.2 Complex Numbers in Polar Form
- •1.3 Four Equivalent Forms to Represent Harmonic Waves
- •1.4 Mathematical Identity
- •1.5 Derivation of Four Equivalent Forms
- •1.5.1 Obtain Form 2 from Form 1
- •1.5.2 Obtain Form 3 from Form 2
- •1.5.3 Obtain Form 4 from Form 3
- •1.6 Visualization and Numerical Validation of Form 1 and Form 2
- •1.8 Homework Exercises
- •1.9 References of Trigonometric Identities
- •1.9.1 Trigonometric Identities of a Single Angle
- •1.9.2 Trigonometric Identities of Two Angles
- •1.10 A MATLAB Code for Visualization of Form 1 and Form 2
- •2.2 Equation of Continuity
- •2.3 Equation of State
- •2.3.1 Energy Increase due to Work Done
- •2.3.2 Pressure due to Colliding of Gases
- •2.3.3 Derivation of Equation of State
- •2.4 Derivation of Acoustic Wave Equation
- •2.5 Formulas for the Speed of Sound
- •2.5.1 Formula Using Pressure
- •2.5.2 Formula Using Bulk Modulus
- •2.5.3 Formula Using Temperature
- •2.5.4 Formula Using Colliding Speed
- •2.6 Homework Exercises
- •3.1 Review of Partial Differential Equations
- •3.1.1 Complex Solutions of a Partial Differential Equation
- •3.1.2 Trigonometric Solutions of a Partial Differential Equation
- •3.2 Four Basic Complex Solutions
- •3.3 Four Basic Traveling Waves
- •3.4 Four Basic Standing Waves
- •3.5 Conversion Between Traveling and Standing Waves
- •3.6 Wavenumber, Angular Frequency, and Wave Speed
- •3.7 Visualization of Acoustic Waves
- •3.7.1 Plotting Traveling Wave
- •3.7.2 Plotting Standing Wave
- •3.8 Homework Exercises
- •4.2 RMS Pressure
- •4.2.1 RMS Pressure of BTW
- •4.2.2 RMS Pressure of BSW
- •4.3 Acoustic Intensity
- •4.3.1 Acoustic Intensity of BTW
- •4.3.2 Acoustic Intensity of BSW
- •4.5.1 Issues with Real Impedance
- •4.6 Computer Program
- •4.7 Homework Exercises
- •4.8 References
- •4.8.1 Derivatives of Trigonometric and Complex Exponential Functions
- •4.8.2 Trigonometric Integrals
- •5.1 Spherical Coordinate System
- •5.2 Wave Equation in Spherical Coordinate System
- •5.3 Pressure Solutions of Wave Equation in Spherical Coordinate System
- •5.4 Flow Velocity
- •5.4.1 Flow Velocity in Real Format
- •5.4.2 Flow Velocity in Complex Format
- •5.5 RMS Pressure and Acoustic Intensity
- •5.7 Homework Exercises
- •6.1 Review of Pressure and Velocity Formulas for Spherical Waves
- •6.2 Acoustic Waves from a Pulsating Sphere
- •6.3 Acoustic Waves from a Small Pulsating Sphere
- •6.4 Acoustic Waves from a Point Source
- •6.4.1 Point Sources Formulated with Source Strength
- •6.4.2 Flow Rate as Source Strength
- •6.5 Acoustic Intensity and Sound Power
- •6.6 Computer Program
- •6.7 Project
- •6.8 Objective
- •6.9 Homework Exercises
- •7.1 1D Standing Waves Between Two Walls
- •7.2 Natural Frequencies and Mode Shapes in a Pipe
- •7.3 2D Boundary Conditions Between Four Walls
- •7.3.1 2D Standing Wave Solutions of the Wave Equation
- •7.3.2 2D Nature Frequencies Between Four Walls
- •7.3.3 2D Mode Shapes Between Four Walls
- •7.4 3D Boundary Conditions of Rectangular Cavities
- •7.4.1 3D Standing Wave Solutions of the Wave Equation
- •7.4.2 3D Natural Frequencies and Mode Shapes
- •7.5 Homework Exercises
- •8.1 2D Traveling Wave Solutions
- •8.1.2 Wavenumber Vectors in 2D Traveling Wave Solutions
- •8.2 Wavenumber Vectors in Resonant Cavities
- •8.3 Traveling Waves in Resonant Cavities
- •8.4 Wavenumber Vectors in Acoustic Waveguides
- •8.5 Traveling Waves in Acoustic Waveguides
- •8.6 Homework Exercises
- •9.1 Decibel Scale
- •9.1.1 Review of Logarithm Rules
- •9.1.2 Levels and Decibel Scale
- •9.1.3 Decibel Arithmetic
- •9.2 Sound Pressure Levels
- •9.2.2 Sound Power Levels and Decibel Scale
- •9.2.3 Sound Pressure Levels and Decibel Scale
- •9.2.4 Sound Pressure Levels Calculated in Time Domain
- •9.2.5 Sound Pressure Level Calculated in Frequency Domain
- •9.3 Octave Bands
- •9.3.1 Center Frequencies and Upper and Lower Bounds of Octave Bands
- •9.3.2 Lower and Upper Bounds of Octave Band and 1/3 Octave Band
- •9.3.3 Preferred Speech Interference Level (PSIL)
- •9.4 Weighted Sound Pressure Level
- •9.4.1 Logarithm of Weighting
- •9.5 Homework Exercises
- •10.1 Sound Power, Acoustic Intensity, and Energy Density
- •10.2.2 Room Constant
- •10.2.3 Reverberation Time
- •10.3 Room Acoustics
- •10.3.1 Energy Density due to an Acoustic Source
- •10.3.2 Sound Pressure Level due to an Acoustic Source
- •10.4 Transmission Loss due to Acoustical Partitions
- •10.4.2 Transmission Loss (TL)
- •10.5 Noise Reduction due to Acoustical Partitions
- •10.5.1 Energy Density due to a Partition Wall
- •10.5.2 Sound Pressure Level due to a Partition Wall
- •10.5.3 Noise Reduction (NR)
- •10.6 Homework Exercises
- •11.1 Complex Amplitude of Pressure and Acoustic Impedance
- •11.1.3 Transfer Pressure
- •11.2 Complex Acoustic Impedance
- •11.3 Balancing Pressure and Conservation of Mass
- •11.4 Transformation of Pressures
- •11.5 Transformation of Acoustic Impedance
- •11.7 Numerical Method for Molding of Pipelines
- •11.8 Computer Program
- •11.9 Project
- •11.10 Homework Exercises
- •12.1.1 Equivalent Acoustic Impedance of a One-to-Two Pipe
- •12.2 Power Transmission of a One-to-Two Pipe
- •12.3 Low-Pass Filters
- •12.4 High-Pass Filters
- •12.5 Band-Stop Resonator
- •12.6 Numerical Method for Modeling of Pipelines with Side Branches
- •12.7 Project
- •12.8 Homework Exercises
- •Nomenclature
- •Appendices
- •Appendix 1: Discrete Fourier Transform
- •Discrete Fourier Transform
- •Fourier Series for Periodical Time Function
- •Formulas of Discrete Fourier Series
- •Appendix 2: Power Spectral Density
- •Power Spectral Density
- •Accumulated Sound Pressure Square
- •Sound Pressure Level in Each Band
- •References
- •Index

192 7 Resonant Cavities
1
pRMS ¼ p jAj
2
Solve for Plmn using the given RMS pressure ( pRMS ¼ 1 [Pa]) and the location
(x ¼ 2 [m], y ¼ 1 [m], and z ¼ 0 [m]) as shown below: |
5 |
||||||||||
1 ½Pa& ¼ p2 jAj |
¼ p2 Plmn cos |
5 cos |
5 |
¼ p2 Plmn cos 2 |
|||||||
|
|
1 |
|
|
1 |
|
π |
π |
|
1 |
π |
|
|
|
2 |
|
|
|
|
|
|
|
|
Plmn |
¼ |
p |
5 |
|
½ & |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
||||
|
|
|
|
Pa |
|
|
|
|
|
|
|
|
|
2 π |
|
|
|
|
|
|
|
||
7.5Homework Exercises
Exercise 7.1 (OPEN-CLOSED PIPE)
A pipe with OPEN-CLOSED boundary conditions has a finite length L as shown below. Set the left end of the pipe as x ¼ 0:
|
|
|
|
|
|
|
|
= 0 |
|
|
|
= |
|||
(a)Show that the formulas for the wavenumber and natural frequency of the eigenmode l are:
π
kl ¼ 2L ð2l 1Þ
c
f l ¼ 4L ð2l 1Þ
(b) If L ¼ 0.5 [m],determine the first three natural frequencies, and plot their corresponding mode shapes. Use 340 [m/s] for the speed of sound.

7.5 Homework Exercises |
193 |
Use 340 [m/s] for the speed of sound (c) in air. Show units in the Meter- Kilogram-Second (MKS) system.
(Answers) (b) 170 [Hz], 510 [Hz], 850 [Hz]
Exercise 7.2 (CLOSE-OPEN PIPE)
A pipe with OPEN-CLOSED boundary conditions has a finite length L as shown below. Set the left end of the pipe as x ¼ 0:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
= |
|||
(a)Show that the formulas for the wavenumber and natural frequency of the eigenmode l are:
kl ¼ 2πL ð2l 1Þ, f l ¼ 4cL ð2l 1Þ
(b)If L ¼ 0.5 [m],determine the first three natural frequencies, and plot their corresponding mode shapes. Use 340 [m/s] for the speed of sound.
Use 340 [m/s] for the speed of sound (c) in air. Show units in the Meter- Kilogram-Second (MKS) system.
(Answers) (b) 170 [Hz], 510 [Hz], 850 [Hz]
Exercise 7.3 (3D Rectangular Cavity)
The dimensions of a rectangular cavity are (Lx, Ly, Lz) ¼ (2, 5, 10)[m].
(a)Calculate all resonant frequencies of this cavity that are lower than 60 Hz.
(b)Plot the mode shape of the eigenmode (l, m, n) ¼ (0, 3, 5) using the pressure nodal lines, and indicate the peaks and valleys with “+” and “-” signs, respectively.
(c)Plot the mode shape of the eigenmode (l, m, n) ¼ (0, 5, 8) using the pressure nodal lines, and indicate the peaks and valleys with “+” and “-” signs, respectively.

194 |
7 Resonant Cavities |
Use 340 [m/s] for the speed of sound (c) in air. Show units in the Meter- Kilogram-Second (MKS) system.
(Answers): (a) 17 [Hz], 34 [Hz], 38.01 [Hz], 48.08 [Hz], 51 [Hz]
Exercise 7.4 (3D Rectangular Cavity)
The dimensions of a rectangular cavity are (Lx, Ly, Lz) ¼ (3, 4, 10)[m].
(a)Calculate all resonant frequencies of this cavity that are lower than 50 [Hz].
(b)Plot the mode shape of the eigenmode (l, m, n) ¼ (0, 2, 3) using the pressure nodal lines, and indicate the peaks and valleys with “+” and “-” signs, respectively.
(c)Plot the mode shape of the eigenmode (l, m, n) ¼ (0, 5, 8) using the pressure nodal lines, and indicate the peaks and valleys with “+” and “-” signs, respectively.
Use 340 [m/s] for the speed of sound (c) in air. Show units in the Meter- Kilogram-Second (MKS) system.
(Answers): (a) 17 [Hz], 34 [Hz], 42.5 [Hz], 45.8 [Hz]
Exercise 7.5 (3D Rectangular Cavity)
The dimensions of a rectangular cavity are (Lx, Ly, Lz) ¼ (4, 6, 10)[m]. Use 340 [m/s] for the speed of sound.
(a)Calculate the three lowest resonant frequencies of this cavity. Indicate the eigenmode. State the mode numbers.
(b)Plot the mode shape of the eigenmode (l, m, n) ¼ (0, 3, 5) using the pressure nodal lines, and indicate the peaks and valleys with “+” and “-” signs, respectively.
(Answer): (a) f001 ¼ 17 [Hz]; f010 ¼ 28.33 [Hz]; f011 ¼ 33.04 [Hz]
Exercise 7.6 (Standing Waves, Complex) (Optional)
!
Derive the 2D velocity vector usðx, y, tÞ of the plane standing wave from the 2D acoustic pressure using Euler’s force equation. Use complex number format in the derivation:
pðx, y, tÞ ¼ |
1 |
AtAxAy e jðωtþθt Þ þ e jðωtþθt Þ |
8 |
∙ e jðkxxþθxÞ þ e jðkxxþθxÞ ∙ e jðkyyþθyÞ þ e jðkyyþθyÞ
|
b |
e jðωtþθt Þ e jðωtþθt Þ |
|
!uSðx, y, tÞ ¼ |
nxex |
||
8ρ0c AtAxAy |

7.5 Homework Exercises |
195 |
∙ e jðkxxþθxÞ e jðkxxþθxÞ ∙ e jðkyyþθyÞ þ e jðkyyþθ
nybey AtAxAy e jðωtþθt Þ e jðωtþθt Þ
8ρ0c
∙ e jðkxxþθxÞ þ e jðkxxþθxÞ ∙ e jðkyyþθyÞ e jðkyyþθ
Use Euler’s force equation:
|
pðx, y, tÞ ¼ ρo |
∂ ! |
|
|
|
|
||||
|
|
uSðx, y, tÞ |
||||||||
∂t |
||||||||||
!uSðx, y, tÞ ¼ ρo |
Z ∂x pðx, y, tÞ dt |
ρo |
Z ∂y pðx, |
|||||||
|
ex |
|
∂ |
ey |
|
∂ |
||||
|
b |
|
|
|
|
|
b |
|
|
|
yÞ
yÞ
y, tÞ dt
Chapter 8
Acoustic Waveguides
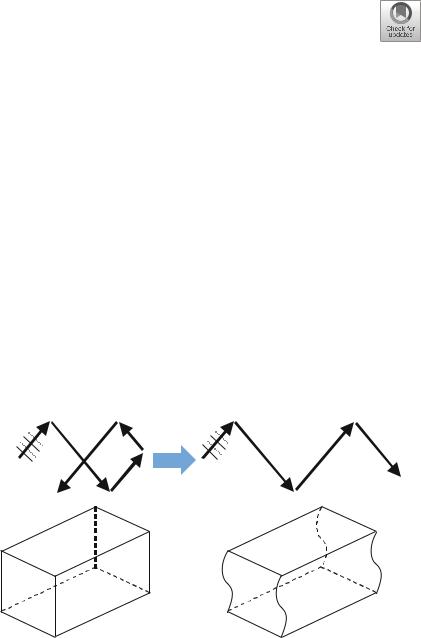
In the previous chapter, resonance in rectangular cavities was formulated as standing waves as a result of the addition of a forward traveling wave (pre-reflection) and a backward traveling wave (post-reflection). In this chapter, we will study the propagation of plane waves in acoustic waveguides, as shown on the right-hand side of the figure below. In acoustic waveguides, traveling waves propagate along waveguides and have no returning waves; standing waves exist in lateral directions.
We can treat acoustic waveguides as resonant cavities with the two ends removed (see the figure below). Because there is no reflecting wave on the two ends, the wave in the waveguide will propagate without returning waves (as shown on the righthand side of the figure below):
Resonant Cavity |
Acoustic Waveguide |
||
|
|
|
|
|
|
|
|
© The Author(s), under exclusive license to Springer Nature Switzerland AG 2021 |
197 |
H. Lin et al., Lecture Notes on Acoustics and Noise Control, https://doi.org/10.1007/978-3-030-88213-6_8
198 |
8 Acoustic Waveguides |
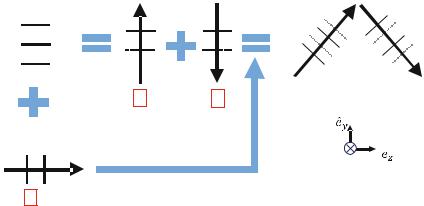
The propagation of plane waves in acoustic waveguides is in the form of resonance (standing waves in the transverse direction) and propagation (traveling waves in the axial direction). Based on what we learned from the previous chapters, we can treat a standing wave (shown in the upper left of the figure below) as the addition of two traveling waves with the same amplitudes and traveling in opposite directions. By adding these two traveling waves (in the transverse direction) back to the traveling wave (in the axial direction), we can reconstruct the propagating wave in the acoustic waveguide as shown in the upper right of the figure below:
|
|
Standing Wave |
Traveling |
|
Traveling |
Waves Propagate in |
|
|
|||||||||||||||||||||||
(In Transverse Dir.) |
|
Acoustic Waveguide |
|
|
|||||||||||||||||||||||||||
|
Wave |
|
|
|
Wave |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+2 |
|
1+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Traveling Wave |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(In Axial Dir.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
After the two walls in the z-direction are removed, the four wavenumber vectors (in 2D resonant cavities as shown in the previous chapter) become two wavenumber vectors because there is no reflection in the z-direction as shown in the figure above. Without the two walls in the z-direction, the wavenumbers in the y-direction are still discretized (as in 2D resonant cavities), but the wavenumbers in the z-direction become continuous numbers as:
kym ¼ |
π |
|
is DISCRETIZED where m is an INTEGER |
|||
|
m |
kym |
||||
Ly |
||||||
kzn ¼ |
π |
n |
¼ kz |
kz |
is CONTINOUS since Lz can be ANY LENGTH |
|
|
||||||
Lz |
||||||
In a waveguide, because Lz can be considered as a very large number, and based on the formula above, kzn is continuous. The formulas shown above are the most important formulas of this chapter and will be derived in detail in this chapter.
