Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5173 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Башкирский Государственный Аграрный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
акустика / lin_h_bengisu_t_mourelatos_zp_lecture_notes_on_acoustics_and.pdf
Скачиваний:
154
Добавлен:
04.05.2023
Размер:
12.68 Mб
Скачать
☆
►Содержание►

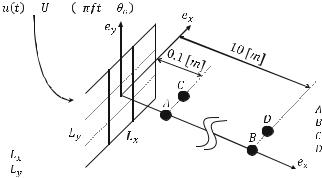
6.8 Objective

161

 

 

m

f ¼ 340 ½Hz&; U ¼ 30 h

 

i; θo ¼ 0 ½rad&

s

= cos 2 +

̂

 

 

 

 

 

Use m × n point sources

̂

 

 

 

 

 

m=3 (x-direction)

 

 

 

 

 

 

 

 

n=3 (y-direction)

 

 

 

 

 

 

 

at (0,

0, 0.1) [m]

 

 

at (0,

0, 10) [m]

 

 

at (0.1, 0, 0.1) [m]

 

 

at (0.1, 0, 10) [m]

= 0.9 [m]

 

 

̂

 

= 0.6 [m]

 

 

 

Drawing not to scale

 

 

 

 

 

 

 

Divide the rectangular plate into m sections in the x-direction and n sections in the y-direction as:

m ¼ 3;

n ¼ 3

Use a time resolution of t ¼ 0.0001 [s] for the time history plot.

Use the function POINTSOURCE.m and the main program VibrationPlate.m to complete this project.

Write your group report and submit it as a single pdf file that includes the following items:

6.8Objective

1)Procedures

2)Your completed MATLAB script.

3)Output figures of the sound pressure at points A, B, C, and D

4)Output figures of the flow velocity at points A, B, C, and D

5)Comparison of the pressures at points A and B

6)Comparison of velocities at points A and C

7)Conclusion of the simulation results

Hint: This project is an extension of Example 6.3. You can use Example 6.3 as a reference for this project.

162

6 Acoustic Waves from Spherical Sources

6.9Homework Exercises

Exercise 6.1

An acoustic pressure p(r, t) is created by a surface vibration of a spherical source with a radius a ¼ 12 ½m&. At a distance of r ¼ 10 [m], the following sound pressure is given:

1

 

1

 

1

1

pðr ¼ 10, tÞ ¼ 0:02 cos

 

πct þ

 

 

π ½Pa& ¼

Re 0:02e jð8πctþ4πÞ ½Pa&

8

4

Answer the following questions:

a)What are the angular frequency ω and the wave number k of the radiation?

b)Calculate the sound pressure at any point in space outside of the sphere.

c)Calculate the flow velocity at any point in space outside of the sphere.

d)Calculate the surface velocity of the spherical source.

e)Calculate the sound intensity at any point outside of the sphere.

f)Calculate the sound power radiated from the source.

g)What are the period and wavelength of the radiation?

Use 415 [rayls] for the characteristic impedance (ρ0c) of air and 340 [m/s] for the speed of sound in air. Show units in the Meter-Kilogram-Second (MKS) system.

(Answers):

 

 

 

 

 

 

 

ω ¼ 8 πc sec ;

k ¼

 

8

π m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

rad

 

 

1

 

rad

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

pðr, tÞ ¼

 

 

0:2 cos

 

 

 

 

 

πct

 

 

 

 

πr þ 1:5π ½Pa&

 

r

8

8

 

 

 

1

 

 

0:2

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

m

uðr, tÞ ¼

 

 

 

 

 

 

cos

 

 

 

πct

 

 

 

πr þ 1:5π

ϕh

 

i;

r

ρoc cos ðϕÞ

8

8

s

where cos ðϕÞ ¼

 

 

π r

 

 

 

; ϕ ¼ tan 1 π8r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8

1

π8r 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

þ

ð

Þ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

uðtÞ ¼ 0:005 cos

 

 

πct þ

0:9992πh

 

i

 

 

 

8

s

 

 

 

 

 

 

 

 

 

 

 

I r

4:82 10 5

 

 

 

 

w

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ð Þ ¼

 

 

 

 

 

 

 

 

 

h

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r2

 

 

m2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

w ¼ 6:06 10 4½w&

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T ¼

16

½s&;

λ ¼ 16½m&

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

 

 

 

 

6.9 Homework Exercises

163

Exercise 6.2 (Reverse of Exercise 6.1)

A sound pressure p(r, t) is created by a surface vibration of a spherical source with a radius a ¼ 12 ½m&. Assume that the surface velocity of the sphere is given by:

 

 

1

 

 

m

uðr ¼ a, tÞ ¼

0:005 cos

 

πct þ 0:9992 πh

 

i

8

sec

¼

 

1

 

 

m

Re 0:005 e jð8πctþ0:9992

πÞh s i

Answer the following questions:

a)What are the angular frequency ω and the wave number k of the radiation?

b)Calculate the sound pressure at any point in space outside of the sphere.

c)Calculate the flow velocity at any point in space outside of the sphere.

d)Calculate the sound pressure at r ¼ 10 [m].

e)Calculate the sound intensity at any point outside of the sphere.

f)Calculate the sound power radiated from the source.

Use 415 [rayls] for the characteristic impedance (ρ0c) of air and 340 [m/s] for the speed of sound in air. Show units in the Meter-Kilogram-Second (MKS) system.

(Answers):

 

 

 

 

 

 

 

 

ω ¼ 8 πc sec

;

 

k ¼

8

π m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

rad

 

 

 

1

 

rad

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

pðr, tÞ ¼

 

 

0:2

cos

 

 

πct

 

 

 

πr þ 1:5π ½Pa&

 

r

8

8

 

 

 

1

 

 

0:2

 

 

 

 

 

1

 

 

 

1

 

 

 

 

m

uðr, tÞ ¼

 

 

 

 

 

 

 

cos

 

πct

 

 

 

πr þ

1:5π ϕh

 

i

r

 

ρoc cos ðϕÞ

8

8

s

where cos ðϕÞ ¼

 

 

π r

 

 

 

 

;

 

 

ϕ ¼ tan 1 π8r

 

 

 

 

 

 

 

 

 

 

8

1

π8r 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

þ

ð Þ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

 

pðr ¼ 10m, tÞ ¼ 0:02 cos

 

 

πct þ

 

π ½Pa&

 

 

 

8

4

 

 

 

 

 

 

 

 

 

 

 

 

I r

 

 

4:82 10 5

 

 

 

 

w

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ð Þ ¼

 

 

 

 

 

 

 

h

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r2

 

 

m2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

w ¼ 6:06 10 4½w&

 

 

 

Exercise 6.3

A sound pressure is created by the pulsating surface of a sphere with a radius a ¼

12 ½m&. Assume that the surface velocity of the sphere is:

164

6 Acoustic Waves from Spherical Sources

uðr ¼ a, tÞ ¼ 4 cos 2πct

where c is the speed of the sound. At a distance r sphere, calculate the following:

a)Sound pressure amplitude

b)Sound intensity

c)Sound power (or sound pressure)

πh m i

2sec

¼5 [m] from the center of the

Note: This pulsating sphere cannot be treated as a small sphere source or a point source.

Use 415 [rayls] for the characteristic impedance (ρ0c) of air and 340 [m/s] for the speed of sound in air. Show units in the Meter-Kilogram-Second (MKS) system.

(Answers): (a) 158.18 [Pa]; (b) 30:15 mw2 ; (c) 9470.5 [w]

Exercise 6.4 (Point Source)

The sound pressure p(r, t) is created by a surface vibration of a spherical source with the radius a ¼ 201 ½m&. Assume that the surface velocity of the sphere is given by:

1

 

m

uðr ¼ a, tÞ ¼ 0:5 cos 8

πct þ πh

 

i

sec

1

m

¼ Re 0:5 e jð8πctþπÞh i

s

Treat this small spherical source as a point source to answer the following questions:

a)What are the angular frequency ω and the wave number k of the radiation?

b)Calculate the source strength at r ¼ a and r ¼ 2a from the center of the sphere.

c)Use the source strength to calculate flow velocity u(r, t) at any point in space.

d)Use the source strength to calculate sound pressure p(r, t) at any point in space.

e)Calculate the sound intensity at any point.

f)Calculate the sound power radiated from the source.

Use 415 [rayls] for the characteristic impedance (ρ0c) of air and 340 [m/s] for the speed of sound in air. Show units in the Meter-Kilogram-Second (MKS) system.

(Answers):

ω ¼ 8

πc sec ; wave number : k ¼

8

π m

1

 

rad

1

rad

6.9

Homework Exercises

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

165

a)

 

m3

i; Qs

 

 

 

 

m3

 

 

 

 

 

 

 

 

 

 

 

 

 

Qs ¼ 0:0157 h s

¼ 0:0157 h s i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

0:2

 

1

 

 

 

 

1

 

 

m

 

uðr, tÞ ¼

 

 

 

 

 

 

 

cos

 

 

πct

 

 

 

 

 

 

πr þ 1:5π ϕh

 

i;

 

r

ρoc cos ðϕÞ

8

8

s

where, cos ðϕÞ ¼

 

 

π r

; ϕ ¼ tan 1

8

 

 

 

 

 

 

 

 

 

 

 

8

 

1 π8r 2

π r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

þ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Þ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ð

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

 

pðr, tÞ ¼

 

 

0:2 cos

 

 

πct

 

 

 

 

 

πr þ 1:5π ½Pa&

 

r

8

8

 

 

 

 

 

 

 

 

 

 

I r

5:0 10 5

 

 

 

 

 

w

 

 

 

 

 

 

 

 

 

 

ð Þ ¼

 

 

 

 

 

h

 

i

 

 

 

 

 

 

 

 

 

 

 

 

r2

 

 

m2

w ¼ 6:3 10 4½w&

Exercise 6.5 (Point Source)

A sound pressure p(r, t) is created by a surface vibration of a small spherical source with radius a ¼ 251 ½m&. Assume the surface velocity of the sphere is:

1

 

π m

uðr ¼ a, tÞ ¼ 3 cos

 

πct

2h

 

i

4

sec

Treat this small spherical source as a point source to answer the following questions:

d)Calculate the source strength of the spherical source.

e)Calculate sound pressure p(r, t) at any point in space.

f)Calculate sound intensity at any point in space.

g)Calculate sound power radiated from the source.

Use 415 [rayls] for the characteristic impedance (ρ0c) of air and 340 [m/s] for the speed of sound in air. Show units in the Meter-Kilogram-Second (MKS) system.

(Answers):

a)

Qs ¼ 0:0603 h s

i

 

 

 

 

 

 

 

ð

 

Þ ¼0:0029

 

 

 

m3

 

 

 

 

½

 

&

b)

r, t

 

 

w

 

 

πc t

Pa

p

1:5645

cos

 

 

π r

 

 

 

 

r

 

 

 

 

 

 

 

4

 

4

 

 

c)

IðrÞ ¼ r2

 

 

 

 

 

 

 

 

 

 

 

 

½

 

m2

 

 

 

 

 

 

 

g)

w

¼

0:0371

w

&

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Chapter 7

Resonant Cavities

In the previous chapters, when we calculated the sound pressure radiated from a vibrating surface, we only considered forward waves but not returning waves. This is because we have not considered any reflecting surfaces yet.

From this chapter forward, we will study sound waves that are bouncing inside cavities, waveguides, and pipes. If we consider the pre-reflection waves as forward waves, the post-reflection waves will be backward waves. The resulting wave of the addition of a pre-reflection forward wave and its post-reflection backward wave is a standing wave because the amplitudes of the pre-reflection wave and its postreflection wave are (almost) the same.

In resonant cavities, the standing waves caused by the pre-reflection forward wave and the post-reflection backward wave will cause the air in the cavity to be resonant at certain frequencies. The resonance of air in cavities, if not considered properly, can be a serious design flaw. On the other hand, the resonance of cavities, if understood correctly, can be used as vibration absorbers in filter designs (Chapter 13).

In this chapter, natural (resonant) frequencies and their corresponding mode shapes of resonant cavities will be formulated. The discretized natural frequencies and mode shapes will be derived from standing wave solutions with constraints on boundary conditions. It can be difficult to fully comprehend and visualize standing waves in rectangular cavities because they propagate in 3D space. It is easier to first understand and formulate standing waves in 1D than in 3D. For this reason, we will first study the 1D standing waves between two walls and then extend the formulas to 2D and 3D.

A summary of formulas of 1D standing waves between two walls is listed below and will be derived in Section 7.1:

The natural frequency of an eigenmode (l, m, n) in an enclosure is:

© The Author(s), under exclusive license to Springer Nature Switzerland AG 2021

167

H. Lin et al., Lecture Notes on Acoustics and Noise Control, https://doi.org/10.1007/978-3-030-88213-6_7

Соседние файлы в папке акустика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности