72 8 Application of Chaos Theory to Acoustical Imaging
|
|
u S F |
−→ |
|
|
Ae |
|
+ |
|
|
|
− |
|
|
|
|
R |
|
dw /(dw −1) |
(8.17) |
||||
|
|
|
|
|
|
|
t |
|
|
exp |
|
1 |
|
|||||||||||
|
|
|
r |
|
= |
|
j (kx x |
|
ky y ) |
· |
|
dw/ d f |
· |
|
− |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dw |
|
|
|||||
where R = |
absolute distance between the coordinates of a scatterer within the breast |
|||||||||||||||||||||||
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
r |
= |
x |
, y |
|
and a sampling point, the starting point of random walk. |
|
||||||||||||||||||
(−→ |
|
|
|
|||||||||||||||||||||
In this work, A is taken to be unity, and the value of t for every scatterer is taken to be 1. The average GSPD P ( R, t ) is obtained by taking the average of each probability value obtained for all R, that is, all scatterers with respect to a sampling point. The total ultrasound Þeld within the object is given by the summation of the incident Þeld and the scattered Þeld:
u(−→r ) = u0(−→r ) + us F (−→r ) |
|
|
|
|
|
|
|
|
|
dw /(dw −1) |
|||
|
|
|
|
|
|
|
R |
|
|||||
= |
Ae j (kx x +k+y y ) |
+ |
Ae j (kx x +ky y ) |
· |
t −dw/ d f exp |
− |
|
|
|
|
|
||
|
|
|
|
||||||||||
|
|
|
1 |
||||||||||
|
|
|
|
2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
t |
|
|
|
||||
|
|
|
|
|
|
dw |
|||||||
(8.18)
By substituting the total Þeld into the LippmannÐSchwinger integral [16], the Þnal expression is given by
|
|
u (r ) |
|
r |
−→r n |
|
−→r |
u |
|
−→r |
u |
|
−→r |
d−→r |
(8.19) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
s = |
g |
− |
|
|
|
|
|
|
o |
|
+ S F |
|
|
|
|
−→ |
= |
object function, u |
s −→ |
= |
scattered Þeld. |
|
|
|
|
||||||||
where n(r ) |
|
(r ) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(r |
) to solve the LippmannÐ |
|||
So there is no need to omit the scattered Þeld us −→ |
|
|
|
||||||||||||||
Schwinger equation. This scattered Þeld plays a signiÞcant role in the determination of the image resolution.
In diffraction tomography, the next step is to derive the reconstruction algorithm to solve for the object function and generate the image. This is a tedious process as the higher the image resolution, the more object functions will be needed. Hence one has to develop an efÞcient reconstruction algorithm to solve the equations represented in matrix form.
8.11 Discrete Helmholtz Wave Equation
Here the Helmholtz wave equation is solved by Þrst converting it in discrete form. This discrete equation then expresses each sample of the projection data as a summation of all scatterers within the object:
8.11 Discrete Helmholtz Wave Equation |
73 |
u (r ) |
! g r |
−→r |
u(−→r )n(−→r ) |
(8.20) |
s = |
|
|
|
|
− |
|
|
|
r
After taking all the samples of each projection into considerations, a vector equation will be derived from the above equation as
U = A N |
(8.21) |
where
.
U = [us (r1)us (r2) . . . us (rn )T |
|
|||||||||
|
N |
= |
"n r |
n r |
|
. . . n r #T |
|
|||
|
|
g r1 |
1 |
|
2 |
r |
m |
|
|
|
A |
= |
− |
r u |
g(r1 |
− |
r u r |
||||
|
|
|
1 |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
m m |
||
|
|
g rn − r1 u u1 |
g(rn − rm )u(r m) |
|||||||
where n = (1, 2,É) = total number of projections samples and m = (1, 2, É) is total number of scatterers.
The vector U, the projection scattered Þeld can be simulated or measured. For this chapter, it will be simulated. The simulation details will be given in the next section.
The matrix A contains products of the total Þeld and GreenÕs function. The gener-
ated image will represent the object in its surrounding medium. Hence the values of
−→
r are coordinates of both points located in the surrounding medium and the scatterers. A circle of radius R is the boundary of the object. This circle is slightly bigger than the object to be examined. In this way all the scatterers found within this circle are considered to be the object itself. The reason of using a circle is that the interior view of the breast is circular in shape. The total Þeld within this circle will be given by the summation of the scattered Þeld, calculated through fractal approximation. Also the Þeld outside the circle will consist only of the incident Þeld.
The vector N has to be solved. It contains unknown values of both the object function and the surrounding medium. Equation (8.21), a linear algebraic equation can be solved conventionally using the LU decomposition [17] or the Gaussian elimination method when the number of projections and samples involved is small, for instance 32 projections by 32 samples or less. However, such methods are not applicable. When the image resolution is 64 × 64 or above due to the size of matrix A with 4096 rows by 4096 columns is too large for storage in programs like Matlab.
8.12 Kaczmarz Algorithm
When solving equation with large matrices, usually it is assumed that a signiÞcant number of elements within the matrix are zero. So that sparse matrix techniques can be used.
74 |
8 Application of Chaos Theory to Acoustical Imaging |
One possible method of solving large matrices with nonzero elements is the use of the Kaczmarz algorithm [18]. In this algorithm, the problem of memory wastage is solved by operating only one row of the matrix at a time.
This algorithm also guarantees a proper solution of the linear algebraic equation (8.21) with proper convergence. Hence it is able to satisfy the Helmholtz wave equation with proper discretization of all the functions. The Kaczmarz algorithm uses the technique of solving the linear equation U = A.N by representing each row of the vector equation by a separate equation.
For a set of equation consisting of one projection by three samples, it is written
as
−→ |
= |
|
|
−→ −→ −→ |
|
− |
−→ −→ −→ |
||||||||||||
|
−→ − |
|
1 |
|
|
1 |
|
|
1 |
+ |
−→ |
2 |
2 |
n r |
2 |
||||
us ( r1 ) |
|
g r1 |
r |
u r |
n r |
|
g r1 |
|
r |
u r |
|
||||||||
|
+ |
g r1 |
|
−→r )u |
−→r |
n |
−→r |
|
|
|
|
|
|
|
|
||||
|
−→ − |
|
3 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|||
us ( r2 ) |
= |
g r2 |
−→r |
u |
−→r |
n |
−→r |
+ |
g r2 |
− |
−→r |
u r2 |
n |
−→r |
|||||
−→ |
|
−→ − |
|
1 |
|
1 |
|
|
1 |
−→ |
2 |
−→ |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
+ |
g r2 |
|
−→r )u |
−→r |
n |
−→r |
|
|
|
|
|
|
|
|
||||
|
−→ − |
|
3 |
|
3 |
|
|
3 |
|
|
|
−→ −→ −→ |
|||||||
−→ |
= |
|
|
−→ −→ −→ |
|
− |
|||||||||||||
|
−→ − |
|
1 |
|
|
1 |
|
|
1 |
+ |
−→ |
2 |
2 |
n r |
2 |
||||
us ( r3 ) |
|
g r3 |
r |
u r |
n r |
|
g r3 |
|
r |
u r |
|
||||||||
|
+ |
g r3 |
|
−→r u |
−→r n |
−→r |
|
|
|
|
|
|
(8.22) |
||||||
|
−→ − |
|
3 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|||||
Each of the above equations represents a hyperplane in three-dimensional space. The solution is given by the intersection of these planes. The method of the Kaczmarz algorithm by projecting its point onto another hyperplane in sequence to reÞne an initial guess. Each step of the iteration enables the new point to get closer to the Þnal solution. With each row of matrix A represented by ai where i = row number, each projection sample represented by ui and each row of the object function represented by nk , where k = the iteration number, a better estimate of ui = ai .nk is given by
nk+1 = nk − [(ai , nk − ui )/(ai · ai )]ai |
(8.23) |
The following example illustrates the convergence of the Kaczmarz algorithm as shown in Fig8.7. This shows hyperplanes in two-dimensional space. Here the initial guess n, on line AB is Þrst projected onto hyperplanes CD giving a11n1 + a12n2 = u1. A new Estimate n2 is produced on line CD. With the projection of this new estimate onto the line EF, the next new estimate n3 is produced.
One notes that each estimate is getting closer and closer to the solution of these equations which is the intersection point of these two hyperplanes.
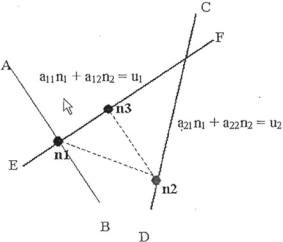
8.13 HounsÞeld Method |
75 |
Fig. 8.7 Convergence of estimates in Kaczmarz [18] Algorithm. After Kaczmarz [18]
8.13 Hounsfield Method
The Kaczmarz algorithm guarantees convergence. However, it has the major concern on the speed of convergence. The interdependency of the row equations is a factor that determines the speed of convergence. If the hyperplanes are perpendicular to each other, the correct answer can be calculated by only one iteration. On the other hand, if they are parallel to each other, this produces very slow speed of convergence and more iterations will be needed. In this case, one needs to orthogonalize the equations to speed up the convergence. However, this method requires a similar amount of storage space and work to Þnd the inverse of matrix A.
Ramarkrishnan [19] proposed a less computationally expensive method, the pairwise orthogonalization method. This method orthogonalized a hyperplane to its previous hyperplane by the following relations:
Ai |
= |
Ai |
Ai |
− |
1 |
" Ai |
. Ai |
− |
1 |
/ Ai |
|
1 Ai |
|
1 |
# |
(8.24) |
|||
$ |
|
− $ |
|
$ |
|
|
$ |
− $ − |
|
|
|
|
|
||||||
and |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bt |
= |
bi |
bi |
1 |
" At |
Ai |
− |
1 |
/ Ai |
1 |
Ai |
− |
1 |
# |
(8.25) |
||||
$ |
|
− $− |
|
|
|
$ · |
|
|
$ − |
|
· $ |
|
|
|
|
||||
This new orthogonal system of equations is represented by A$i and b$i respectively. This method reduces the need for large storage space as only an additional equation is needed at one time although it is not optimum. In fact it has been proven that it would actually reduce the number of iterations by half.
HounsÞeld [20] introduced another alternative method by rearranging the order of equations to reduce the interdependency between adjacent equations. It stated that convergence is slow due to the fact that the hyperplane at adjacent points are usually