ЦТ МАТЕМАТИКА 17-18 2 1

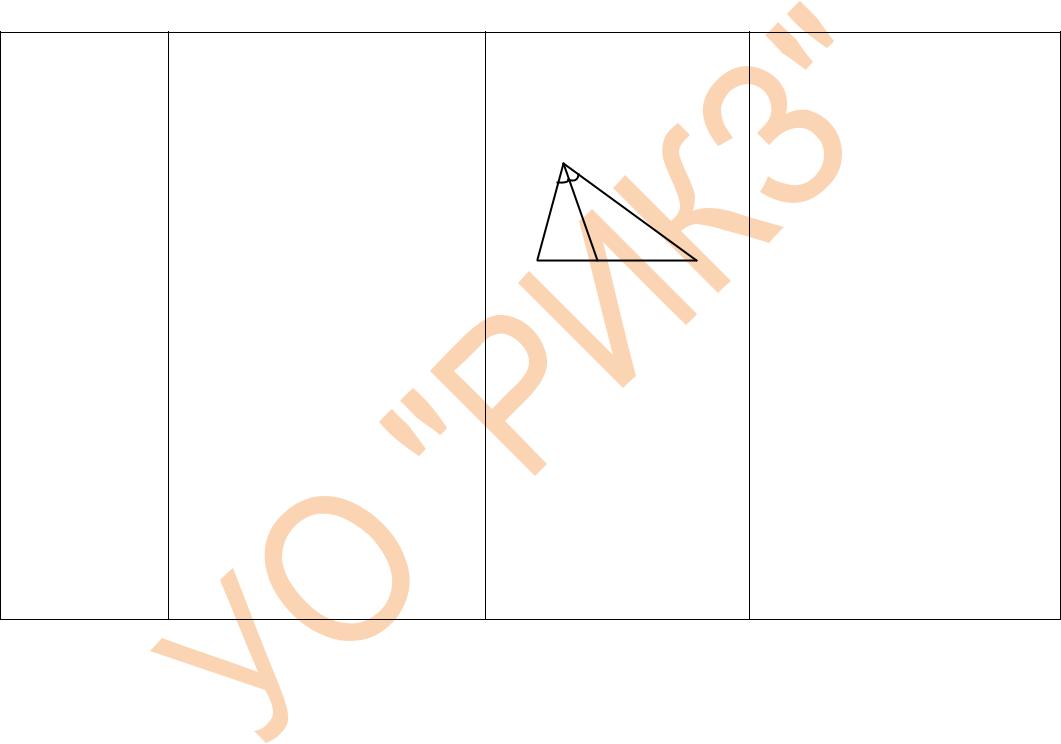
Раздел программы

вступительных

Содержание задания

Комментарий и решение задания

Учебное издание

испытаний/ Элемент

содержания

В9. Один из отрезков, на которые биссектриса

Задание на проверку умения применять

Латотин, Л. А. Математика : учеб. пособие для 8-го кл.

разделила сторону треугольника, оказался равным

свойство биссектрисы треугольника.

учреждений общ. сред. образования с рус. яз.

одной из двух других сторон, длины которых 45 и

Решение:

обучения / Л. А. Латотин, Б. Д. Чеботаревский ; пер. с

75. Найдите длину третьей стороны треугольника

A

белорус. яз. Е. В. Масальской. – 4-е изд., испр. и доп. –

Минск : Народная асвета, 2015. – 407 с. : ил. (П. 24,

с. 235–240);

45

75

Шлыков, В. В. Геометрия : учеб. пособие для 8-го кл.

общеобразоват. учреждений с рус. яз. обучения /

В. В. Шлыков. – 3-е изд., перераб. – Минск : Нар.

B

a

C

асвета, 2011. – 166 с. : ил. (Гл. 3, § 1, с. 110–113)

M

b

Биссектриса любого угла треугольника делит

противолежащую

сторону в

таком

отношении, в каком находятся прилежащие

Геометрические фигуры и

стороны. Тогда

AB

BM

.

их свойства/ Свойство

AC

CM

биссектрисы треугольника

Пусть биссектриса

AM

делит

сторону

BC на отрезки длиной a и b (см. рис.).

Рассмотрим возможные случаи:

1) Пусть

a 45,

тогда

по

свойству

биссектрисы

45

45

,

b 75.

75

b

BC 45 75,

BC 120.

Треугольника со

сторонами 45,

75, 120 не существует.

2) Пусть

b 75,

тогда

по

свойству

биссектрисы

45

a

,

a 45.

75

75

BC 45 75,

BC 120.

Треугольника со

сторонами 45,

75, 120 не существует.

3) Пусть

a 75,

тогда

по

свойству

РТ–2017/2018 гг. Этап II. Вариант 1

Тематическое консультирование по математике

21

Раздел программы

вступительных

Содержание задания

Комментарий и решение задания

Учебное издание

испытаний/ Элемент

содержания

биссектрисы

45

75

,

b 125.

75

b

BC 75 125,

BC 200. Треугольника со

сторонами 45,

75, 200 не существует.

4) Пусть

b 45,

тогда

по

свойству

биссектрисы

45

a

,

a 27.

75

45

BC 27 45,

BC 72.

Треугольник

со

сторонами 45, 72, 75 существует.

Ответ: 72

В10. Найдите

сумму

наименьшего

целого

Задание

на

проверку

умения

решать

Латотин, Л. А. Математика : учеб. пособие для 9-го кл.

положительного

и

наименьшего

целого

рациональные

неравенства

методом

учреждений общ. сред. образования с рус. яз.

отрицательного

решений

неравенства

интервалов.

обучения / Л. А. Латотин, Б. Д. Чеботаревский ; пер. с

1

2

3

0

Решение:

белорус. яз. Л. В. Латотиной. – 4-е изд., испр. и доп. –

1

2

3

Минск : Народная асвета, 2014. – 397 с. : ил. (П. 10,

x 5

2

x

2

25

x

2

5x

Неравенство

x 5 2 x2 25 x2 5x 0

с. 118–121; с. 123–126);

равносильно

неравенству

Алгебра : учеб. пособие для 9-го кл. учреждений общ.

x 15

0

1 .

Неравенство

(1)

сред. образования с рус. яз. обучения / Е. П. Кузнецова

Уравнения и неравенства/

x x 5 2

x 5

[и др.] ; под ред. проф. Л. Б. Шнепермана. – 4-е изд.,

Решение рациональных

решим методом интервалов.

Рассмотрим

испр. и доп. – Минск : Народная асвета, 2014. – 287 с. :

ил. (Гл. 2, п. 2.8, с. 127–136)

неравенств

x 15

функцию

y

;

ее область

x x 5 2 x 5

определения

x 0,

x 5

и x 5, а

ее

нуль – число 15. Отметим на координатной

прямой промежутки знакопостоянства этой

функции

и

укажем

те

значения

x, при

которых

y 0

(см. рис.), то есть решения

неравенства (1).

РТ–2017/2018 гг. Этап II. Вариант 1

Тематическое консультирование по математике

22

Раздел программы

вступительных

Содержание задания

Комментарий и решение задания

Учебное издание

испытаний/ Элемент

содержания

сред. образования с рус. яз. обучения / Е. П. Кузнецова

Суммируя

объемы

выполненных

[и др.] ; под ред. проф. Л. Б. Шнепермана. – 4-е изд.,

каменщиками

работ,

получим

систему

испр. и доп. – Минск : Народная асвета, 2014. – 287 с. :

уравнений

ил. (П. 5, с. 249–259);

xt y t 1 1,

4

1

откуда

находим

Арефьева, И. Г. Алгебра : учеб. пособие для 7-го кл.

учреждений общ. сред. образования с рус. яз. обучения /

x t

y t

1,

5

5

И. Г. Арефьева, О. Н. Пирютко. – Минск : Народная

xt y t 1

4

1

асвета, 2017. – 313 с. : ил. (Гл. 3, § 16, с. 160–174; гл. 4,

x t

y t

,

§ 25, с. 290–301)

5

5

y

4

x

1

y,

4

x

6

y,

4x 6 y,

5

5

5

5

часть

работы:

1

1

2,

2x y

2,

3y

6x

6xy

2x y 12xy 2 .

Подстановкой

в

уравнение (2) значения x

из уравнения (1)

получим

уравнение

3y y 12 y

3y

,

2

2 y 18y2 ,

2y 9y 1 0,

y 0

или

y

1

.

Так

как

y

– производительность

9

у 0 , то

y

1

, тогда

x

3

1

,

x

1

.

9

2

9

6

РТ–2017/2018 гг. Этап II. Вариант 1

Тематическое консультирование по математике

24

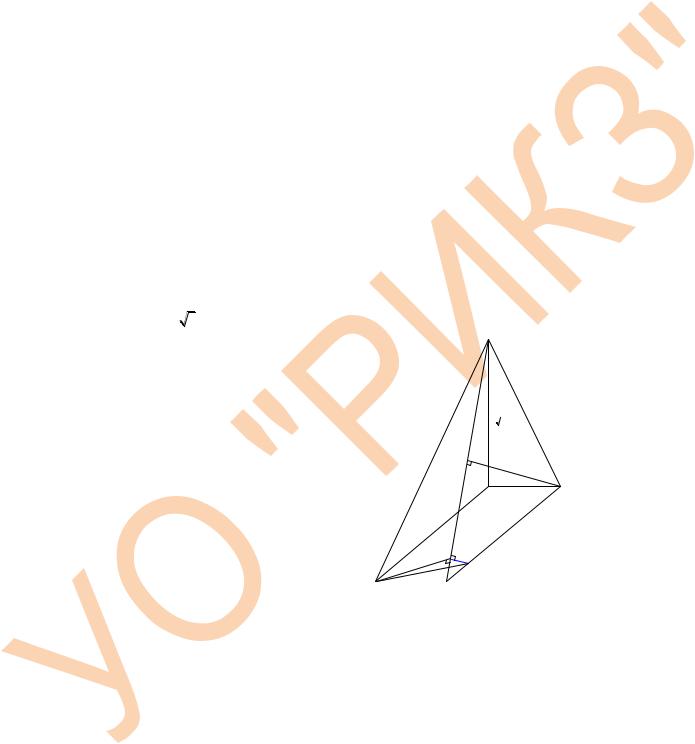
Раздел программы

вступительных

Содержание задания

Комментарий и решение задания

Учебное издание

испытаний/ Элемент

содержания

Подставляя

значения

x

1

и

y

1

в

6

9

уравнение

xt y t 1 1,

найдем время

выполнения всей работы:

1

t

1

t 1 1,

6

9

5

t

10

, t 4 (ч).

18

9

Переведем часы в минуты: 4 ч = 240 мин.

Ответ: 240

В12. В основании

пирамиды SABCD

лежит

Для решения задания необходимо уметь

Латотин, Л. А. Математика : учеб. пособие для 10-го кл.

прямоугольник со сторонами 1 и 5. Боковое

строить линейный угол двугранного угла и

учреждений общ. сред. образования с рус. яз. обучения /

ребро SB

перпендикулярно

плоскости

основания

определять его меру.

Л. А. Латотин, Б. Д. Чеботаревский ; пер. с белорус. яз.

пирамиды

и равно

2 6.

Найдите

значение

Решение:

Л. В. Латотиной. – Минск : Адукацыя і выхаванне, 2013. –

408 с. : ил. (П. 18, с. 260–272);

2

S

выражения

,

где

– линейный

угол

cos

Шлыков, В. В. Геометрия : учеб. пособие для 10-го кл.

двугранного угла при боковом ребре SD

учреждений общ. сред. образования с рус. яз. обучения /

В. В. Шлыков. – 3-е изд., пересмотр. и испр. – Минск :

Нар. асвета, 2013. – 160 с. : ил. (Гл. 3, § 4, с. 138–149)

Геометрические фигуры и

2

6

их свойства/ Двугранный

угол

K

B

C

5

P

M

A

1

D

Так

как

SB ABCD ,

то

треугольники

РТ–2017/2018 гг. Этап II. Вариант 1

Тематическое консультирование по математике

25

Раздел программы

вступительных

Содержание задания

Комментарий и решение задания

Учебное издание

испытаний/ Элемент

содержания

SBA и SBC – прямоугольные и по теореме

Пифагора SA 7,

SC 5. Так

как

ABCD – прямоугольник, то по теореме о

трех перпендикулярах треугольники SAD

Пифагора SD 5

2.

Чтобы

построить

линейный

угол

двугранного угла при боковом ребре

SD,

проведем высоту CK к ребру SD. Так как

треугольник

SCD – прямоугольный

и

равнобедренный

SC DC 5 ,

то

CK DK SK

5

2

.

2

Проведем высоту AP к ребру SD и

найдем

ее

длину.

Так

как

1

7

7

1

SSAD

7 1

,

то

5 2 AP,

2

2

2

2

AP

7

2

.

В

треугольнике

APD

по

10