
ЦТ МАТЕМАТИКА 15-16 э1 вар 1
.pdf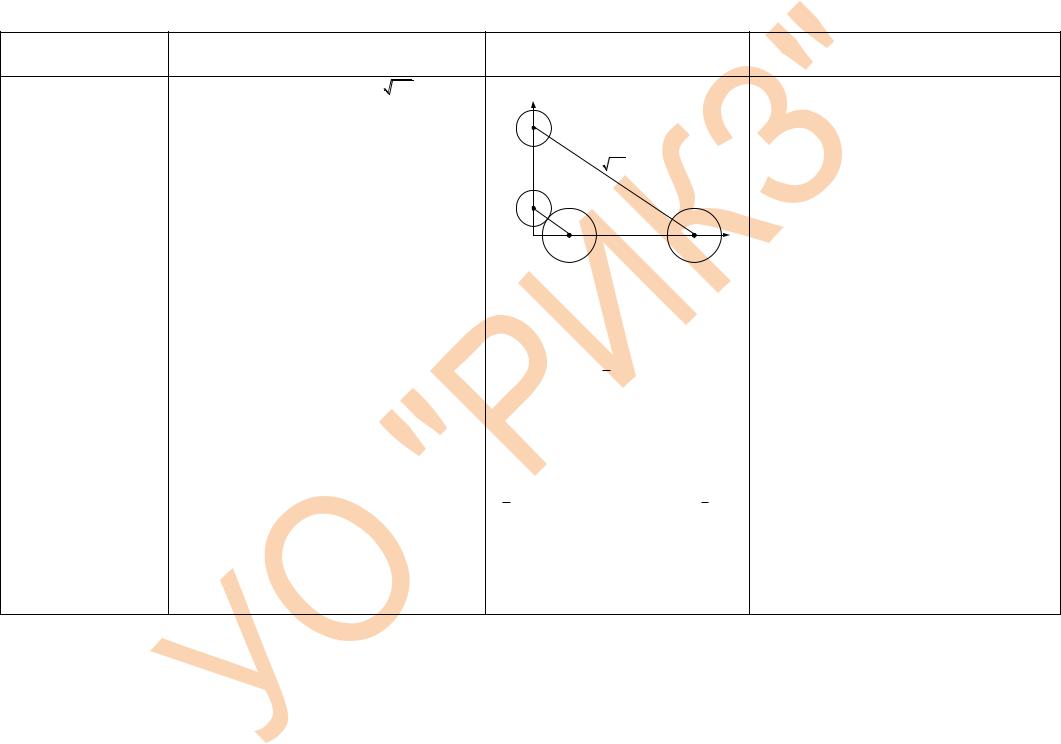
Раздел программы/ |
|
|
|
Содержание задания |
|
|
|
Комментарий и решение задания |
|
Учебное пособие |
|
|||||||||||||
Элемент содержания |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
между центрами шаров |
равно |
292. |
Найдите |
Решение: |
|
|
|
|
|
|
|
|
147); |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(в см/с) |
скорость второго шара, если известно, что |
|
y |
|
|
|
|
|
|
|
|
|
Шлыков, В. В. |
Геометрия |
: |
учеб. |
пособие |
|||||||
через 6 с после начала движения шары столкнулись, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
для 8-го кл. общеобразоват. учреждений с рус. яз. |
|||||||||||||
не |
дойдя |
до |
вершины |
(первоначально |
длины |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
обучения / |
В. В. Шлыков. |
– 3-е изд., |
перераб. – |
||||||||||
отрезков |
AO и BO выражались целыми числами и |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Минск : Нар. асвета, 2011. – 166 с. : ил. (Гл. 2, § 4, |
|||||||||||||
AO BO ) |
|
|
|
|
|
|
|
|
|
|
292 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с. 94–104) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
B |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По условию AO и BO выражаются |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
целыми числами и |
AO2 BO2 |
292, тогда |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
AO 6, |
BO 16. |
Уравнения |
движения |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
центров |
A и |
B шаров запишутся в виде: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x 16 t, y 6 |
1 t. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
момент |
|
столкновения |
|
t 6 с: |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x 16 6 , |
y 6 3 3 |
и |
x2 |
y2 |
25. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Отсюда |
следует, |
|
что 16 6 2 |
9 25, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
значит, |
16 6 4 |
и |
скорость |
шара с |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
центром в точке |
B равна или 2 см/с, или |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
3 1 |
см/с. |
При скорости, |
равной |
|
3 1 |
см/с, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 16 20 4. |
Это |
значит, |
что |
шар |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
радиуса 3 пройдет за вершину угла, что |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
противоречит условию задачи. При |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
скорости, равной 2 см/с, шары столкнутся |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
в положении, указанном на рисунке. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Ответ: 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
21 |

Раздел программы/ |
|
Содержание задания |
|
Комментарий и решение задания |
|
|
|
Учебное пособие |
|
|
||||||||||||||||||||||||||||
Элемент содержания |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
В8. Решите |
уравнение |
2sin2 х sin х 0. В ответ |
Задание на применение алгоритма решения |
Латотин, Л. А. Математика : учеб. пособие |
||||||||||||||||||||||||||||||||||
запишите его корень (в градусах), принадлежащий |
тригонометрического уравнения способом |
для 10-го кл. учреждений общ. |
сред. |
образования |
||||||||||||||||||||||||||||||||||
разложения на множители. |
|
|
|
|
|
|
с |
рус. |
яз. |
обучения |
|
/ |
Л. А. Латотин, |
|||||||||||||||||||||||||
|
|
51π |
|
47π |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
промежутку |
; |
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б. Д. Чеботаревский |
; пер. |
с |
белорус. |
яз. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
10 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
Разложим |
|
левую |
|
часть |
уравнения |
Л. В. Латотиной. – Минск : Адукацыя і выхаванне, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
2sin2 х sin х 0 на множители и получим |
2013. – 408 с. : ил. (П. 23, с. 325–334); |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
sin x(2sin х 1) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгебра : учеб. пособие для 10-го кл. учреждений |
||||||||||||||||||
|
|
|
|
|
|
sin x 0 или 2sin x 1 0. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
общ. |
сред. |
образования с |
рус. |
яз. |
обучения / |
|||||||||||||||||||||
|
|
|
|
|
|
Решим каждое уравнение в отдельности. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Е. П. Кузнецова |
[и |
др.] |
; |
под |
ред. проф. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
sin x 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Л. Б. Шнепермана. – 3-е изд., пересмотр. и испр. |
– |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x n, n Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Минск : Нар. асвета, 2013. – 271 с. : ил. (Гл. 3, |
||||||||||||||
|
|
|
|
|
|
Найдем |
его |
корни, |
|
принадлежащие |
п. 3.9, с. 225–232) |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
51π |
; |
47π |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
промежутку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Уравнения и неравенства/ |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
51 |
|
|
47 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение |
|
|
|
|
|
|
n |
|
, |
5 |
|
n 5 |
. |
Так |
как |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
тригонометрических |
|
|
|
|
|
10 |
|
9 |
|
|
|
10 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n Z, то нет целого значения |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
уравнений |
|
|
|
|
|
n |
на этом |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
промежутке. Значит, уравнение |
sin x 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
на |
промежутке |
|
|
|
51π |
; |
47π |
не |
имеет |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
корней.
2 sin x 1 0,
2 sin x 1, sin x 12 ,
x 1 k 1 |
k, k Z. |
||||
|
|
|
|
6 |
|
Найдем |
его корни из промежутка |
||||
51π |
|
47π |
|
|
|
|
|
; |
|
: |
|
|
9 |
|
|||
10 |
|
|
|
||
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
22 |
Раздел программы/ |
Содержание задания |
Комментарий и решение задания |
Учебное пособие |
|
Элемент содержания |
||||
|
|
|
51 1 k 1 k 47 , 10 6 9
5101 1 k 1 16 k 5 92 .
Только при k 5 получаем |
корень, |
|||||
принадлежащий промежутку |
51π |
; |
47π |
|
, |
|
|
|
|
|
|||
|
10 |
|
9 |
|
|
|
|
|
|
он равен 930°, и других корней нет. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ответ: 930 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В9. Окружность радиуса 3, вписанная в ромб, делит |
Задание на применение формулы площади |
Латотин, Л. А. Математика |
|
: |
учеб. |
пособие |
|||||||||||||||||
одну из диагоналей на отрезки, длины которых |
ромба, |
теоремы |
Пифагора |
и |
свойства |
для 8-го кл. учреждений общ. |
сред. образования |
||||||||||||||||
относятся как 3 : 2 : 3. Найдите площадь ромба |
S, |
высоты |
прямоугольного |
|
треугольника, |
с |
рус. |
яз. |
обучения |
|
/ |
Л. А. Латотин, |
|||||||||||
в ответ запишите значение выражения |
15 S |
|
проведенной к гипотенузе. |
|
|
|
|
Б. Д. Чеботаревский |
; |
пер. |
|
с |
белорус. |
яз. |
|||||||||
|
Решение: |
|
|
|
|
|
|
|
Е. В. Масальской. – 4-е изд., испр. и доп. – Минск : |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Народная асвета, 2015. – 407 с. : ил. (П. 16, с. 149– |
||||||||||
|
|
|
|
|
|
|
K C |
|
|
|
|
156); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
B |
|
M |
x |
x |
N |
|
|
D |
Шлыков, В. В. |
Геометрия |
: |
|
учеб. |
пособие |
|||||
|
|
|
|
3x |
|
2x O |
|
3x |
|
для 8-го кл. общеобразоват. учреждений с рус. яз. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
обучения / |
В. В. Шлыков. – |
3-е изд., |
перераб. – |
|||||||
Геометрические фигуры и |
|
|
|
|
|
|
|
|
|
|
|
Минск : Нар. асвета, 2011. – 166 с. : ил. (Гл. 2, § 2, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
их свойства/ Площадь |
|
|
|
|
|
|
|
|
|
|
|
|
с. 75–86) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ромба |
|
|
Точка O – центр окружности, вписанной в |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ромб ABCD, |
OK |
|
– ее радиус (см. рис.). |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
По условию задачи BM : MN : ND 3 : 2 : 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
и |
MN 6, |
тогда |
|
2x 6, |
x 3. |
Длина |
|
|
|
|
|
|
|
|
|
|
|
|||
диагонали BD ромба ABCD равна 24 (8 3 24).
В прямоугольном |
треугольнике |
BKO : |
BO 12, OK 3, |
тогда по |
теореме |
Пифагора |
|
|
BO2 BK 2 OK 2 , |
144 BK 2 9, |
|
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
23 |
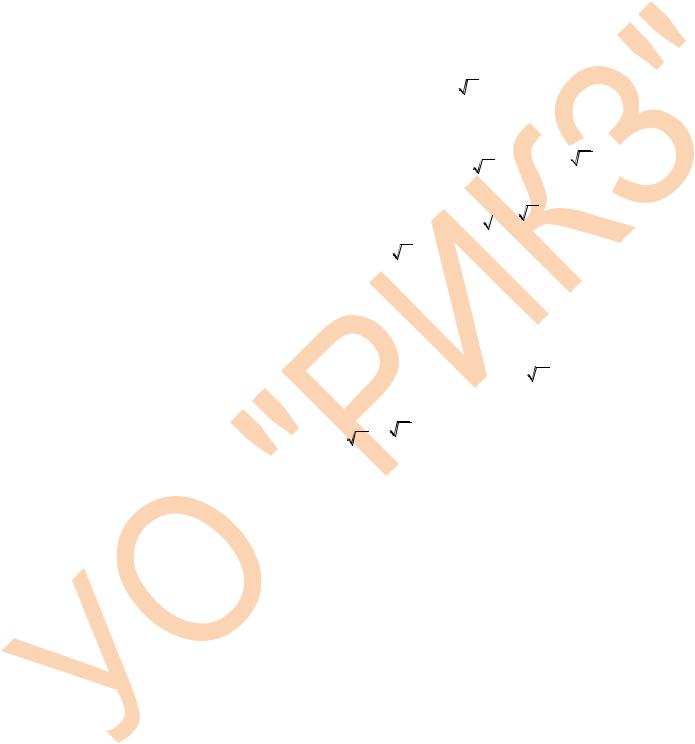
Раздел программы/ |
|
Содержание задания |
|
|
Комментарий и решение задания |
|
|
|
Учебное пособие |
|||||||||||||||||||||||||||||||||||||||||||||
Элемент содержания |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
BK 2 |
135, |
BK 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
прямоугольном |
|
треугольнике |
COB |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
воспользуемся |
|
свойством |
|
|
|
|
|
высоты, |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
проведенной к гипотенузе, и |
|
|
|
получим |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
OK 2 |
BK KC, |
9 3 15 KC, |
|
|
KC |
|
15 |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
BC BK KC, |
BC 3 |
15 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC |
16 |
15 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Высота ромба равна двум радиусам |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
вписанной в него окружности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
нахождения |
|
|
|
|
площади |
|
|
|
|
ромба |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
воспользуемся формулой |
|
S ah, где |
a – |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
длина стороны ромба, h – высота ромба. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Получим S BC 2OK, |
S |
96 |
15 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
ответ |
|
запишем |
|
значение |
|
выражения |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
96 |
15 |
|
96 3 288. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 288 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
В10. Найдите |
количество |
целых |
решений |
Задание на применение алгоритма решения |
Латотин, Л. А. Математика : учеб. пособие |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2x 1 |
|
|
|
5 x |
|
|
|
x 6 |
|
|
неравенства, содержащего переменную под |
для 8-го кл. учреждений общ. сред. образования |
||||||||||||||||||||||||||||||||||||||||
|
неравенства |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Уравнения и неравенства/ |
|
|
|
|
|
|
|
|
|
|
|
|
знаком модуля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
рус. |
яз. |
обучения |
/ |
Л. А. Латотин, |
||||||||
Решение неравенств, |
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б. Д. Чеботаревский ; пер. |
с |
белорус. яз. |
|||||||||
которые содержат |
|
|
|
|
|
|
|
|
|
|
|
|
Нанесем |
|
на координатную |
прямую |
те |
Е. В. Масальской. – 4-е изд., испр. и доп. – Минск : |
||||||||||||||||||||||||||||||||||||
переменную под знаком |
|
|
|
|
|
|
|
|
|
|
|
|
значения x, при которых |
|
|
|
|
каждое |
Народная асвета, 2015. – 407 с. : ил. (П. 6, с. 55–62); |
|||||||||||||||||||||||||||||||||||
модуля |
|
|
|
|
|
|
|
|
|
|
|
|
выражение, |
стоящее под знаком модуля в |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
неравенстве |
|
2x 1 |
|
|
|
5 x |
|
|
|
x |
6 |
|
, |
равно |
Алгебра : учеб. пособие для 8-го кл. учреждений |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
общ. |
сред. |
образования с рус. |
яз. обучения / |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
24 |
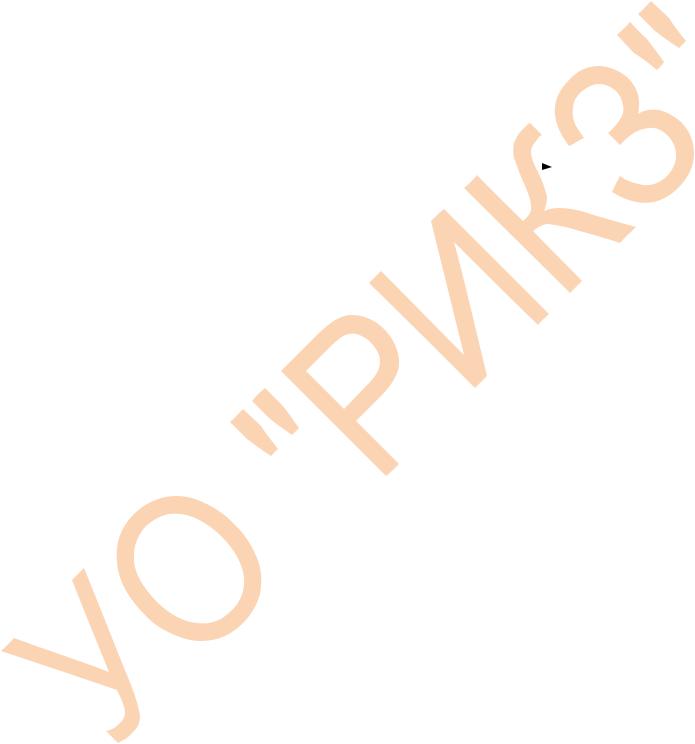
Раздел программы/ |
Содержание задания |
|
Комментарий и решение задания |
|
Учебное пособие |
|||||||||||||||||||||||||||||
Элемент содержания |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нулю, |
это значит |
x 6, |
|
|
x |
1 |
|
|
|
и |
x 5 |
Е. П. Кузнецова [и др.] ; под ред. проф. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Л. Б. Шнепермана. – 4-е изд., испр. и доп. – Минск : |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Народная асвета, 2015. – 310 с. : ил. (Гл. 3, п. 3.3, |
||
|
|
(см. рис.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с. 91–98) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рассмотрим |
|
исходное |
неравенство |
|
на |
|
||||||||||||||||||||||||||
|
|
каждом из полученных промежутков. |
|
|
|
|||||||||||||||||||||||||||||
|
|
1) |
x 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Неравенство |
|
2x 1 |
|
|
|
5 x |
|
|
|
x 6 |
|
|
примет |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
вид |
(2x 1) (5 x) (x 6) 0, |
0 0. |
|
|||||||||||||||||||||||||||||
|
|
Решений нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2) 6 x |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Неравенство |
|
2x 1 |
|
|
|
5 x |
|
|
|
x 6 |
|
|
примет |
|
||||||||||||||||||
|
|
вид (2x 1) (5 x) (x 6) 0, |
x 6. |
|
||||||||||||||||||||||||||||||
|
|
Решением является промежуток ( 6; |
1 |
|
|
|||||||||||||||||||||||||||||
|
|
|
. |
|
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3) |
|
1 |
x 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Неравенство |
|
2x 1 |
|
|
|
5 x |
|
|
|
x 6 |
|
|
примет |
|
||||||||||||||||||
|
|
вид 2x 1 (5 x) (x 6) 0, |
x 5. |
|
|
|
||||||||||||||||||||||||||||
|
|
Решением является промежуток ( |
|
1 |
;5). |
|
||||||||||||||||||||||||||||
|
2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4) |
x 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Неравенство |
|
2x 1 |
|
|
|
5 x |
|
|
|
x 6 |
|
|
примет |
|
||||||||||||||||||
|
|
вид |
|
|
2x 1 (5 x) (x 6) 0, |
0 0. |
|
|||||||||||||||||||||||||||
|
|
Решений нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
25 |
Раздел программы/ |
|
Содержание задания |
|
Комментарий и решение задания |
|
|
Учебное пособие |
|||||||||||||||
Элемент содержания |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Таким образом, решением исходного |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
неравенства является промежуток ( 6 ; 5). |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Целые |
решения: |
5, 4, 3, 2, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1, 0, 1, 2, 3, 4. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Их количество равно 10. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Ответ: 10 |
|
|
|
|
|
|
|
|
|
|
|
|
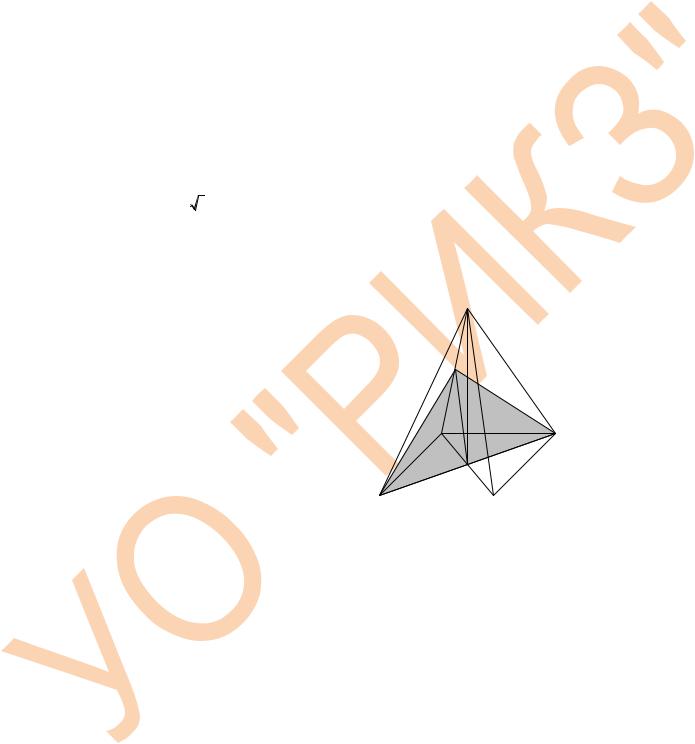
В11. В |
правильной |
четырехугольной |
пирамиде |
Задание |
на |
построение |
сечения |
Латотин, Л. А. Математика : учеб. пособие |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
пространственных |
геометрических фигур |
для 10-го кл. учреждений общ. сред. образования с |
|||||||||
|
сторона |
основания |
равна |
6, |
а каждое боковое |
|||||||||||||||||
|
плоскостью, на определение угла между |
рус. |
яз. |
обучения |
/ |
Л. А. Латотин, |
||||||||||||||||
|
ребро наклонено к плоскости основания под углом, |
|||||||||||||||||||||
|
прямой и |
плоскостью, |
на |
применение |
Б. Д. Чеботаревский ; пер. |
с |
белорус. яз. |
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
формул площади треугольника. |
Л. В. Латотиной. – Минск : Адукацыя і выхаванне, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
равным |
arccos 4 . |
Через |
диагональ |
основания |
|||||||||||||||||
|
Решение: |
|
|
|
|
|
2013. – 408 с. : ил. (П. 3, с. 36–45); |
|
||||||||||||||
|
параллельно боковому ребру проведена плоскость. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Найдите |
площадь полученного |
сечения пирамиды |
|
|
|
|
|
|
|
Шлыков, В. В. |
Геометрия |
: |
учеб. пособие |
||||||||
|
этой плоскостью |
|
|
|
|
|
|
|
|
|
S |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
для 10-го кл. учреждений общ. сред. образования с |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рус. яз. обучения / В. В. Шлыков. – 3-е изд., |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пересмотр. и испр. – Минск : Нар. асвета, 2013. – |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
160 с. : ил. (Гл. 1, § 4, с. 40–52) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
Геометрические фигуры и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
их свойства/ Сечение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
многогранников |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Через точку О (точка пересечения |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
диагоналей основания пирамиды) в |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
плоскости SBD проведем прямую OM |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
параллельно боковому ребру |
SD. Так как |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
точка O – середина BD, |
то отрезок ОМ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
26 |
Раздел программы/ |
Содержание задания |
|
|
Комментарий и решение задания |
|
Учебное пособие |
|||||||||||||||||||||||||||||||
Элемент содержания |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
является |
|
|
средней |
линией |
|
|
|
треугольника |
|
||||||||||||||||||||||||||
|
|
|
SBD |
|
|
|
|
|
|
(по |
|
|
|
|
теореме |
|
Фалеса) |
и |
|
||||||||||||||||||
|
|
OM |
1 |
SD |
(1). |
|
|
ОМ |
и |
АС |
образуют |
|
|||||||||||||||||||||||||
|
2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
плоскость АМС, параллельную боковому |
|
||||||||||||||||||||||||||||||||||
|
|
ребру |
|
SD |
(см. рис.). Треугольник АМС – |
|
|||||||||||||||||||||||||||||||
|
|
искомое сечение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
В |
равнобедренном |
треугольнике |
АМС |
|
|||||||||||||||||||||||||||||||
|
|
AM MC |
|
медиана |
ОМ |
|
|
|
является |
и |
|
||||||||||||||||||||||||||
|
|
высотой, тогда площадь сечения можно |
|
||||||||||||||||||||||||||||||||||
|
|
найти |
|
по |
формуле |
SAMC |
1 |
AC OM . |
С |
|
|||||||||||||||||||||||||||
|
|
2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
учетом |
|
равенства |
(1) |
|
|
получаем, что |
|
||||||||||||||||||||||||||||
|
|
|
SAMC |
|
1 |
|
AC SD |
(2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Длина |
|
|
|
диагонали |
АС |
квадрата |
ABCD |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
равна |
|
|
|
|
|
|
|
|
|
|
|
|
2 AB, |
|
|
|
|
|
|
|
то |
|
есть |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
AC |
|
|
|
2 |
6, |
|
|
AC 2 3. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Рассмотрим |
прямоугольный |
|
|
треугольник |
|
||||||||||||||||||||||||||||||
|
|
SOD : по условию |
cos SDO |
|
1 |
, |
тогда |
|
|
||||||||||||||||||||||||||||
|
4 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
AC |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
DO |
|
1 |
|
|
, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
cos SDO |
, |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
SD |
4 |
|
SD |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
3 |
, |
|
|
SD 4 |
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
SD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Подставим полученные |
|
значения |
AC |
и |
|
||||||||||||||||||||||||||||||
|
|
|
SD в формулу (2) и найдем, что площадь |
|
|||||||||||||||||||||||||||||||||
|
|
сечения равна 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Ответ: 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
27 |

Раздел программы/ |
Содержание задания |
Комментарий и решение задания |
|
|
Учебное пособие |
|
|||||||||||
Элемент содержания |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
В12. На доске выписаны натуральные числа |
Задание на числа и числовые зависимости, |
Латотин, Л. А. Математика : учеб. пособие |
||||||||||||||
|
большие 100, но меньшие 600, которые обладают |
на |
|
применение |
правила |
деления |
для 9-го кл. учреждений общ. сред. образования с |
||||||||||
|
следующими тремя свойствами: при делении на 4 и |
натуральных чисел с остатком. |
|
|
рус. |
яз. |
обучения |
|
|
/ |
Л. А. Латотин, |
||||||
|
на 6 дают в остатке 3, а при делении на 9 дают в |
Решение: |
|
|
|
Б. Д. Чеботаревский |
; |
пер. |
с |
белорус. яз. |
|||||||
|
остатке 6. Количество этих чисел равно … |
По |
условию задачи |
числа l |
имеют вид |
Л. В. Латотиной. – 4-е изд., испр. и доп. – Минск : |
|||||||||||
|
|
l 4n 3 6m 3 9k 6, где n, m, k N. |
Народная асвета, 2014. – 397 с. : ил. (П. 19, с. 232– |
||||||||||||||
|
|
Первое такое трехзначное число равно 123, |
234); |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
следующее за ним – |
159, третье число – |
Алгебра : учеб. пособие для 9-го кл. учреждений |
|||||||||||||
|
|
195 и так далее. Последовательность этих |
|||||||||||||||
|
|
общ. |
сред. |
образования |
с |
рус. яз. обучения / |
|||||||||||
|
|
чисел представляет собой арифметическую |
|||||||||||||||
|
|
Е. П. Кузнецова [и |
др.] |
; |
под |
ред. проф. |
|||||||||||
|
|
прогрессию, первый |
член которой |
равен |
|||||||||||||
|
|
Л. Б. Шнепермана. – 4-е изд., испр. и доп. – Минск : |
|||||||||||||||
Уравнения и неравенства/ |
|
123, |
а |
|
разность d 159 123 36 |
и n -й |
|||||||||||
|
|
Народная асвета, 2014. – 287 с. : ил. (Гл. 4, п. 4.3, |
|||||||||||||||
Задачи о соотношениях |
|
член |
|
|
an 123 36(n 1). |
Найдем |
|||||||||||
|
|
|
с. 202) |
|
|
|
|
|
|
|
|||||||
между числами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
количество членов данной прогрессии, |
|
|
|
|
|
|
|
|
||||||||
|
|
меньших 600. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
123 36(n 1) 600, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
36n 36 477, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
36n 513, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n |
513 |
, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n 14 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Количество чисел равно 14. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Ответ: 14 |
|
|
|
|
|
|
|
|
|
|
|
||||
____________________________
Предлагается одно из возможных решений задания. Ответы к заданиям даны с учетом правил заполнения бланка ответов
____________________________
Электронные версии учебных изданий размещены в разделе «Электронные версии учебников» (http://e-padruchnik.adu.by) национального образовательного портала (www.adu.by)
РТ–2015/2016 гг. Этап I. Вариант 1 |
Тематическое консультирование по математике |
28 |
