27. Статистическое распределение выборки. Полигон частот и гистограмма частот.

Полигон распределения (дословно — многоугольник распределения) строится в прямоугольной системе координат. Величина признака откладывается на оси абсцисс, частоты или относительные частоты — по оси ординат. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но их можно применять также для интервальных рядов. В этом случае на оси абсцисс откладываются точки, соответствующие серединам данных интервалов.

Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:

X			…..
w			….

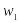
где относительные частоты .

статистическое распределение –

X			…..
n			….

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты и соединяют точки отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) .

27. Эмпирическая функция распределения.

Понятие функции распределения было дано в разделе теории вероятности для случайной величины. Для выборки вводится понятие эмпирической функции распределения. Эмпирическая функция распределения (функция распределения выборки) это функция F^*(x), которая определяет для каждого значения x_i относительную частоту события X<x. Эмпирическая функция распределения имеет вид:

,

где: n_x – число вариант меньших х, n – объём выборки.

В отличие от эмпирической функции распределения для выборки, вводится понятие теоретической функции распределения для генеральной совокупности – F(x). Теоретическая функция распределения определяет вероятность события X<x. Эмпирическая функция распределения F^*(x) по вероятности стремится к теоретической функции распределения F(x) при больших количествах испытаний и обладает всеми свойствами F(x):

1. Значения эмпирической функции принадлежат отрезку F^*(x) Î [0;1].

2. F^*(x) – неубывающая функция.

3. Если х₁ – наименьшая варианта, то F^*(x)=0 при x ≤ x₁.

4. Если х_k – наибольшая варианта, то F^*(x)=1 при x > x_k.

30. Статистические оценки параметров распределения. Несмещенная, эффективная и состоятельная оценки.   Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистические оценки параметров распределения должны удовлетворять следующим требованиям: состоятельности, несмещённости, эффективности.  Состоятельной называют статистическую оценку, которая при неограниченном увеличении числа наблюдений стремится по вероятности к оцениваемому параметру.  Несмещённой называют статистическую оценку, если её математическое ожидание равно оцениваемой характеристике независимо от числа наблюдений. Несмещённая статистическая оценка называется эффективной, если она имеет минимально возможную дисперсию.  Эффекти́вная оце́нка в математической статистике — несмещенная статистическая оценка, дисперсия которой совпадает с нижней гранью в неравенстве Крамера-Рао.