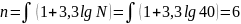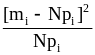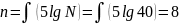- •Равномерный закон распределения:
- •Нормальный закон распределения:
- •Равномерный закон распределения:
- •Нормальный закон распределения:
- •Равномерный закон распределения:
- •Нормальный закон распределения:
- •Равномерный закон распределения:
- •Нормальный закон распределения:
- •Критерий Колмогорова:
- •Ответы на контрольные вопросы:
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра технической кибернетики
ОТЧЕТ
по лабораторной работе №1.
по дисциплине «Моделирование»
«Построение оценок законов распределения случайных величин по выборочным данным»
Проверил:
Гвоздев В. Е.
Вариант 17.
Цель работы: Приобретение практических навыков построения строгих монотонных функциональных зависимостей по выборочным данным.
Задание на работу:
По выборочным
данным проверить их соответствие
следующим законам распределения по
критериям
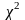 и Колмогорова:
и Колмогорова:
- экспоненциальному
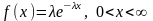 ,
,
- равномерному
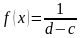 .
.
- Нормальному

Ход работы:
Исходная выборка:
Значение выборки
№ варианта |
17 |
1 |
11 |
2 |
14 |
3 |
45 |
4 |
58 |
5 |
29 |
6 |
80 |
7 |
11 |
8 |
18 |
9 |
88 |
10 |
75 |
11 |
95 |
12 |
73 |
13 |
88 |
14 |
66 |
15 |
81 |
16 |
48 |
17 |
72 |
18 |
73 |
19 |
5 |
20 |
6 |
21 |
89 |
22 |
34 |
23 |
78 |
24 |
48 |
25 |
87 |
26 |
57 |
27 |
98 |
28 |
60 |
29 |
56 |
30 |
24 |
31 |
44 |
32 |
75 |
33 |
91 |
34 |
26 |
35 |
38 |
36 |
2 |
37 |
19 |
38 |
27 |
39 |
54 |
40 |
78 |
Xmin=2
Xmax=98
Разобьем интервал [2; 98] на n=6 равных частей: [2,18), [18,34), [34,50), [50,66), [66,82), [82,98).
Экспоненциальный закон распределения:
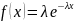 ,
,
параметр
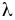 которого рассчитывается по формуле:
которого рассчитывается по формуле:
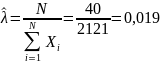
Рассчитаем значения mi и pi. Результаты сведем в таблицу.
Номер интервала |
mi |
pi |
Npi |
|
1 |
6 |
0.25 |
10 |
1.6 |
2 |
6 |
0.19 |
7.6 |
0.33 |
3 |
6 |
0.14 |
5.6 |
0.03 |
4 |
5 |
0.1 |
4 |
0.25 |
5 |
10 |
0.07 |
2.8 |
18.5 |
6 |
7 |
0.055 |
2.2 |
10.47 |
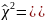
По заданному уровню
значимости
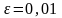 найдем
найдем
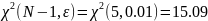 .
Сопоставив
.
Сопоставив
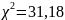 с
с
 =15.09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
экспоненциальному закону распределения,
противоречит фактическим данным.
=15.09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
экспоненциальному закону распределения,
противоречит фактическим данным.
Равномерный закон распределения:
 ,
,
где {d,c} – Верхняя и нижняя границы интервала возможных значений случайной величины).
Рассчитаем значения mi и pi. Результаты сведем в таблицу.
Номер интервала |
mi |
pi |
Npi |
|
1 |
6 |
0.167 |
6.68 |
0.07 |
2 |
6 |
0.167 |
6.68 |
0.07 |
3 |
6 |
0.167 |
6.68 |
0.07 |
4 |
5 |
0.167 |
6.68 |
0.42 |
5 |
10 |
0.167 |
6.68 |
1.65 |
6 |
7 |
0.167 |
6.68 |
0.02 |
По заданному уровню
значимости
найдем
.
Сопоставив
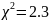 с
=15.09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
равномерному закону распределения,
согласуется с фактическими данными.
с
=15.09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
равномерному закону распределения,
согласуется с фактическими данными.
Нормальный закон распределения:
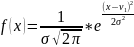 ,
,
где
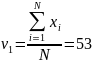
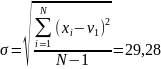
Рассчитаем значения mi и pi. Результаты сведем в таблицу.
Номер интервала |
mi |
pi |
Npi |
|
1 |
6 |
0.37 |
14.8 |
5.23 |
2 |
6 |
0.19 |
7.6 |
0.34 |
3 |
6 |
0.13 |
5.2 |
0.12 |
4 |
5 |
0.12 |
4.8 |
0.008 |
5 |
10 |
0.16 |
6.4 |
2.03 |
6 |
7 |
0.27 |
10.8 |
1.34 |
Желтым – ошибка.
По заданному уровню
значимости
найдем
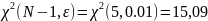 .
Сопоставив
.
Сопоставив
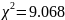 с
=15,09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
нормальному закону распределения,
согласуется с фактическими данными.
с
=15,09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
нормальному закону распределения,
согласуется с фактическими данными.
Xmin=2
Xmax=98
Разобьем интервал [2; 98] на n=8 равных частей: [2,14), [14,26), [26,38), [38,50), [50,62), [62,74), [74,86), [86,98).
Экспоненциальный закон распределения:
,
параметр которого рассчитывается по формуле:
Рассчитаем значения mi и pi. Результаты сведем в таблицу.
Номер интервала |
mi |
pi |
Npi |
|
1 |
5 |
0.19 |
7.6 |
0.89 |
2 |
4 |
0.16 |
6.4 |
0.9 |
3 |
4 |
0.12 |
4.8 |
0.13 |
4 |
5 |
0.099 |
3.96 |
0.27 |
5 |
5 |
0.08 |
3.2 |
1.01 |
6 |
4 |
0.06 |
2.4 |
1.06 |
7 |
6 |
0.05 |
2 |
8 |
8 |
7 |
0.04 |
1.6 |
18.23 |
По заданному уровню
значимости
найдем
.
Сопоставив
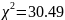 с
=15.09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
экспоненциальному закону распределения,
противоречит фактическим данным.
с
=15.09,
можем заключить, что гипотеза о том, что
выборочные данные соответствуют
экспоненциальному закону распределения,
противоречит фактическим данным.