
ВОПРОСЫ и ЗАДАЧИ К ЭКЗ ПО ВМ 20-21 (1)
.pdf
ЛИНЕЙНАЯ АЛГЕБРА, ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ВОПРОСЫ
1. |
Найти действительные решения уравнения |
x y ixy i |
|||||||||||||||||
2. |
Найти действительные решения уравнения |
xy x y i 4 |
|||||||||||||||||
3. |
Нарисуйте область Re z Im z 0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arg z |
|
|
|
|||||||
|
|
|
|
|
|
|
4 |
|
3 |
|
|||||||||
4. |
Нарисуйте область |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Im z 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
z |
1 |
|
|
|
|||||||
5. |
Нарисуйте область |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Re z 2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Нарисуйте линию |
|
z 2 i |
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
Нарисуйте линию |
|
z 1 i |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
8. |
Что больше? arg(1+2i) или arg(2+i)? |
|
|
||||||||||||||||
9. |
Что больше? arg(-3-2i) или arg(-2-3i)? |
|
|||||||||||||||||
10. |
Что больше? |
|
11 12i |
|
или 10 13i |
? |
|
||||||||||||
|
|
|
|||||||||||||||||
11. |
Что больше? |
|
1 2i или |
|
2 i |
|
? |
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12.
13.
z |
i |
2e |
|
|
8 |
z |
i |
2e |
|
|
6 |
,
,
тогда
тогда
Re z
Re z
4
6
,
,
Im
Im
z
z
4
6
=?
=?
14. Если
|
|
i |
|
|
z 3e |
2 |
, |
||
|
||||
|
|
|
то
Im |
1 |
|
z |
||
|
=?
15. |
z1 |
|
2e |
i |
, |
|
8 |
||||||
|
|
|
|
|
z |
2 |
|
|
|
|
|
||
3 cos |
|
|
i sin |
|
|
|
|
4 |
|
|
4 |
, тогда
z |
2 |
|
|
1 |
|
z |
2 |
|
=?
16. |
z1 |
|
2e |
i |
, |
|
8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
||
z2 |
3 cos |
|
|
i sin |
|
, тогда |
|
=? |
|
|
|
2 |
|||||||
|
|
|
4 |
|
|
4 |
|
z1 |
|
17. |
2 3i 3 2i ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18. |
2 3i |
? |
|
|
|
|
|
|
|
|
|
|
3 2i |
|
|
|
|
|
|
|
|
|
|
||
|
|
z |
|
2 5i z 5 1 i 0 |
|
|
|
|
|
|||
19. |
Решить уравнение |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
20. |
Решить уравнение |
z |
4 |
5z |
2 |
36 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
21. |
Решить уравнение |
z |
2 |
4z 13 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
22. |
det A3x3 5,det 2A3x3 ? |
|
|
|
|
|
|
|||||
23. |
det A 8,det B 2,det( AB 1 ) ? |
|
|
|
|
|
||||||
24. |
A,B,C- матрицы. Сколько столбцов содержит матрица В, если |
0 |
1 |
1 |
? |
|||||||
A 2BТ 3С |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
25.A,B,C- матрицы A3xp B5 xn Cmx4 .m, n, p ?
26.A,B,C- матрицы Amxp B5 x3 C7 xn .m, n, p ?

27.
1 |
2 |
10 |
20 |
40 |
50 |
3 30 60
=?
|
1 |
2 |
3 |
|
2 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28. |
7 |
4 |
69 4 |
7 |
69 ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
3 |
6 |
|
3 |
0 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29. |
Решить систему уравнений |
x 2 y 3 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2x |
4 y 6 |
|
|
|
|
|
|
|
|||
30. |
Система |
ax 2 y 4 |
НЕ вырождена. а=? |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
8x ay 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
31. |
Коллинеарны ли векторы |
3i |
2 j k |
и |
AB , где А(-7;4;3), В(-1;0;1)? |
|
|
|||||||||||||||
с |
|
|
||||||||||||||||||||
32. |
АВСDпараллелограмм. |
DA BA BC DC ? |
|
, 45 |
|
, |
||||||||||||||||
33. |
Может ли вектор образовывать с координатными осями углы 30 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34. |
Чему равна проекция вектора k 3i |
на вектор |
2 j ? |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35. |
Какова ориентация тройки векторов |
b, b |
? |
|
|
|
|
|||||||||||||||
a, a |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36. |
3, b |
|
b |
|
b |
? |
|
|
|
|
|
|
|
|
|
|
|
|||||
a |
2, a |
6, a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
37. |
3, b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a |
2, a |
0, a b ? |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
38. |
Укажите направляющий вектор прямой 2х=3у |
|
|
|
|
|
||||||||||||||||
39. |
Укажите направляющий вектор прямой у=3х+2 |
|
|
|
|
|||||||||||||||||
40. |
Укажите вектор нормали к прямой |
x 1 |
|
y |
|
|
|
|
|
|
||||||||||||
|
2 |
3 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x 2 t |
|
|
|
|
|
|
|
||||
41. |
|
|
|
|
|
|
|
|
|
|
|
y 1 |
? |
|
|
|
|
|
|
|
||
Пересекает ли ось ОХ прямая |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 3t |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||
42. |
Укажите направляющий вектор прямой |
|
x 1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
||
43. |
Укажите направляющий вектор прямой |
|
1 |
2z 0 |
|
|
|
|
||||||||||||||
|
|
x 0 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ЗАДАЧИ
2 3 2i 7 i3
1. Вычислить в показательной форме
3 i
 3 4 2 2i 5
3 4 2 2i 5
2. |
Вычислить |
6 |
3i |
|
|
|
|
|||
1 i |
|
|
|
|
|
|||||
3. |
Решить уравнение |
|
z 8 |
1 |
|
|
||||
|
z 4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4. |
Решить уравнение z 2 z |
0 |
|
|
||||||
5. |
|
3 6 |
1 |
1 |
|
3 2 1 |
|
|||
det |
|
|
|
|
2 |
|
|
? |
||
|
|
|
|
3 |
|
|
1 0 |
|
|
|
|
2 0 |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
?

|
|
1 |
0 |
4 0 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
det 0 |
3 |
2 |
|
|
|
|
1 ? |
|
|
|
|
|
|
|
|
||
6. |
3 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
Найти проекцию вектора |
с 1; 3;1 на ось вектора b |
12i |
16 j |
15k |
|
|
|||||||||||
8. |
Найти угол ABC |
в треугольнике ABC , если А(-1,-2,4), И(-4,-2,0), С( 3,-2,1) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
Найти площадь параллелограмма, построенного на векторах |
a 2; 2; 3 , b |
4i |
6k |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Компланарны ли векторы |
1; 2;3 , b 0; 3;4 , c i |
|
j |
k |
|
|
|
|
|
|||||||||
a |
|
|
|
|
|
|||||||||||||
11. |
Проверьте, лежат ли в одной плоскости точки А(0;1;-2), И(3;1;-1), С (2;4;-4), Д(4;7;-6) |
|||||
12. |
x 2 y 4 |
|
||||
Решить матричным методом |
|
|
|
|
|
|
|
3x y 9 |
|
||||
13. |
4x 3y 7 |
|
||||
Решить матричным методом |
|
|
|
|
|
|
|
5x 2 y 3 |
|
||||
|
|
|
|
|
|
|
|
|
2x 3y 2z 9 |
||||
14. |
По формулам Крамера найти х: |
|
|
|
|
|
x 2 y 3z 14 |
||||||
|
|
|
3x 4 y z 16 |
|||
|
|
|
||||
|
|
|
|
|
|
|
|
|
3x 2 y 3z 3 |
||||
15. |
По формулам Крамера найти у: |
|
|
2x |
7 y z |
0 |
|
|
|||||
|
|
|
|
3x |
8y z |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2x 3y 5z 0 |
||||
16. |
Решить систему методом Гаусса |
|
|
|
|
|
3x 2 y z 0 |
||||||
|
|
|
x |
y 4z |
0 |
|
|
|
|
||||
|
|
|
|
|
||
|
|
2x 3y z 4 |
||||
17. |
Решить систему методом Гаусса |
|
x y 3z |
5 |
||
|
||||||
|
|
|
|
|
|
|
|
|
|
3x 5y 5z 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3y 5z 9 |
||
|
18. |
Решить систему методом Гаусса |
|
|
5 |
|||||
|
2x y 2z |
|||||||||
|
|
|
|
|
|
|
|
|
x 2 y 3z |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 y z 1 0 |
|
|
19. |
Составить каноническое уравнение прямой |
|
|||||||
|
|
|
|
|
|
|
|
|
3x y z 9 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20. |
Составить уравнение плоскости, проходящей через прямую х-1=у+2 =z и точку (1;2;3) |
||||||||
|
21. |
Составить уравнение плоскости, проходящей через точку (-1;4;0) и ось OZ. |
||||||||
|
22. |
При каких α и β прямая |
x 1 |
4 |
y 2z перпендикулярна плоскости 6x 2 y z 5 |
|||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
23. |
Проверьте, лежит ли прямая 2x y 1 z в плоскости 4x y z 1 0 |
||||||||
|
|
|
|
|
|
|
|
|
ТЕОРИЯ ПРЕДЕЛОВ |
|
|
|
|
|
|
|
|
|
|
ВОПРОСЫ |
|
1. |
lim ( ) = 2, lim |
3+ ( ) |
= 5, lim ( ) = ? |
|
||||||
|
|
|||||||||
|
→0 |
→0 |
( ) |
→0 |
|
|
|
|||
2. |
lim ( ) = 2, |
lim ( ( ) ( ) + 3) = 11, lim ( ) = ? |
||||||||
0
?
→0 |
→0 |
→0 |

3. |
lim ( ) = 2, |
lim (3 ( ) − 4 ( )) = −2, lim ( ) =? |
|||||
|
→ 0 |
→ 0 |
2− ( ) |
|
→ 0 |
||
4. |
lim ( ) = 3, |
lim |
= 4, |
lim ( ) = ? |
|||
( ) |
|
||||||
|
→ 0 |
→ 0 |
|
→ 0 |
|||
5.lim ( ) = 3, lim ( ) = 7, lim ( ( )) =?
|
→−1 |
→3 |
→−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
lim ( ) = 5, |
lim ( ( ) ( ) − 3) = 7, lim ( ) =? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
→ 0 |
→ 0 |
|
|
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
lim ( ) = 5, |
lim (3 ( ) − 4 ( )) = −5, lim ( ) =? |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
→ 0 |
→ 0 |
|
|
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
lim ( ) = +∞, lim |
( ) = − ∞, lim (3 ( ) − 4 ( )) =?, lim (4 ( ) + 3 ( )) =? |
|||||||||||||||||||||||||||
|
→ 0 |
→ 0 |
|
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ 0 |
|||||||
9. |
lim ( ) = +∞, lim |
( ) = − ∞, lim ( ) ( ) =?, lim |
|
( ) |
=? |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
→ 0 |
→ 0 |
|
→ 0 |
|
|
|
|
→ 0 |
|
( ) |
|
|||||||||||||||||
10. |
lim ( ) = +∞, lim |
( ) =0, lim ( ) ( ) =?, lim |
|
( ) |
|
=? |
|
|
|||||||||||||||||||||
|
( ) |
|
|||||||||||||||||||||||||||
|
→ 0 |
→ 0 |
→ 0 |
|
|
|
→ 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
11. |
lim ( ) = 0, |
lim ( ) = ∞, lim ( ) ( ) =?, |
|
lim |
( ) |
=? |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
→ 0 |
→ 0 |
→ 0 |
|
|
→ 0 |
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12. |
lim ( ) = +∞, lim |
( ) = ≠ 0, lim ( ) ( ) =?, lim |
|
( ) |
|
=? |
|||||||||||||||||||||||
|
( ) |
||||||||||||||||||||||||||||
|
→ 0 |
→ 0 |
|
→ 0 |
|
|
|
|
|
|
→ 0 |
|
|
||||||||||||||||
13. |
lim ( ) = +∞, lim |
( ) = ≠ 0, lim ( ) ( ) =?, lim |
|
( ) |
|
=? |
|||||||||||||||||||||||
|
( ) |
||||||||||||||||||||||||||||
|
→ 0 |
→ 0 |
|
→ 0 |
|
|
|
|
|
|
→ 0 |
|
|
||||||||||||||||
14. |
lim ( ) = 2, lim ( ) = 5, lim ( ( )) =? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
→ 0 |
→2 |
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
15. |
lim ( ) = +∞, lim |
( ) =1, lim ( ) ( ) =? , lim ( ) ( ) =? |
|||||||||||||||||||||||||||
|
→ 0 |
→ 0 |
→ 0 |
|
|
|
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
16. |
Проверьте с помощью определения предела, что lim(2 + 3) = 5 . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
Проверьте с помощью определения предела, что lim(2 − 3) = 1 . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
→2 |
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18. |
Проверьте с помощью определения предела, что lim |
|
= 0,5 . |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
→∞ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
19. |
Проверьте с помощью определения предела, что lim |
−3 |
|
= |
1 |
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
→∞ |
3 |
|
|
|
|
3 |
|
|
|
|
||||||||||
20. |
Верно ли утверждение, что > 0 ( ) > 0: ( : 0 < | − 1| < ( ) | 3 + 3 − 4| < )? |
||||||||||||||||||||||||||||
21. |
Верно ли утверждение, что > 0 ( ) > 0: ( : 0 < | + 1| < ( ) | 3 + 3 − 4| < )? |
||||||||||||||||||||||||||||
22. |
Верно ли утверждение, что > 0 ( ): > ( ) | |
−1 |
| < ? |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+2 |
|
|||||||||
23. |
Верно ли утверждение, что > 0 ( ): > ( ) |
|
1 |
|
|
< ? |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2+1 |
|
|
|
|
|
|
+2 |
|
|||||||||||||||
24. |
В окрестности каких точек функция ( ) = |
будет БМВ(ББВ)? |
|||||||||||||||||||||||||||
−2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
25. |
В окрестности каких точек функция ( ) = |
+3 |
|
будет БМВ(ББВ)? |
|||||||||||||||||||||||||
2+3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
26. |
В окрестности каких точек функция ( ) = |
2−1 |
является БМВ или ББВ? |
||||||||||||||||||||||||||
−2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
27. |
В окрестности каких точек функция ( ) = |
|
−1 |
|
является БМВ или ББВ? |
||||||||||||||||||||||||
|
+3 |
|
|||||||||||||||||||||||||||
|
Сравните БМВ = − 2 и = ( − 2)2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
29. |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сравните БМВ = + 2 и = √ + 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
30.Сравните БМВ ( ) = sin2x, ( ) = − в окрестности точки = .
31.Сравните БМВ ( ) = −3, ( ) = −2 при → ∞.
32.Сравните бесконечно малые последовательности = +21 , = 2.
33.Существует ли lim =? Если да – будет ли он конечным?
|
→∞ |
|
|
|
2 |
|
|
|
|
||||
34. |
Существует ли lim ln(1 + |
) =? Если да – будет ли он конечным? |
|||||||||||
|
|
||||||||||||
|
→∞ |
|
|
|
|
|
|
||||||
35. |
Существует ли lim |
=? Если да – будет ли он конечным? |
|||||||||||
|
|
|
|
||||||||||
|
→0 |
|
|
|
|
|
|
||||||
|
|
|
|
1+2 +3 2 |
|
|
|
||||||
36. |
Существует ли lim |
|
|
|
|
|
=? Если да – будет ли он конечным? |
||||||
|
|
|
|
|
|||||||||
|
→∞ |
2+2 +3 |
|
|
|
||||||||
37. |
Существует ли lim |
+2 2+3 3 |
|
=? Если да – будет ли он конечным? |
|||||||||
3+2 +3 |
|
||||||||||||
|
→0 |
|
|
|
|||||||||
38. |
Существует ли lim |
2 2+3 3+ |
4 |
=? Если да – будет ли он конечным? |
|||||||||
3+2 2+3 |
|||||||||||||
|
→0 |
|
|||||||||||
39. |
Существует ли lim |
|
2 2+3 3+ 4 |
=? Если да – будет ли он конечным? |
|||||||||
|
|
3+2 2+3 |
|
|
|||||||||
|
→∞ |
|
|
|
|||||||||
40. |
Существует ли lim |
|
2 2+3 3+4 |
=? Если да – будет ли он конечным? |
|||||||||
|
|
|
|
|
|
|
|
||||||
|
→∞ 2+ 3+3 4 |
|
|
|
|||||||||

41. |
Существует ли lim |
2 2+3 3 |
|
=? Если да – будет ли он конечным? |
|||||||
3+3 4 |
|||||||||||
|
→0 |
|
|
||||||||
42. |
Существует ли lim |
1 |
=? |
Если да – будет ли он конечным? |
|||||||
|
|
||||||||||
|
→0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
43. |
Существует ли lim |
1 |
|
=? |
Если да – будет ли он конечным? |
||||||
|
|||||||||||
|
→0 |
|
|
|
|
||||||
44. |
Существует ли lim |
1− |
=? Если да – будет ли он конечным? |
||||||||
|
|||||||||||
|
→∞ |
|
|
||||||||
45. |
2 2 − 2 + 1 ≤ ( ) ≤ 2 . lim ( ) =? |
||||||||||
|
|
|
|
|
|
|
|
|
|
→1 |
|
46. 1 − 2 ≤ ( ) ≤ 2 − 2 . lim ( ) =?
|
→1 |
||||||||||||||||||||||||||||||
47. ≤ ( ) ≤ 2 − . lim ( ) =? |
|||||||||||||||||||||||||||||||
|
→ /2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАЧИ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Вычислить предел lim 5 (√ |
2 − 3 |
|
− √ |
2 − 1). |
||||||||||||||||||||||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Вычислить предел lim 5 (√ − 3 − √ − 1). |
||||||||||||||||||||||||||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. |
Вычислить предел lim |
( 5 −1)( √1+ 2−1) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
1− 2 |
|||||||||||||||||||||||||
|
→0 |
|
|
|
|
|
|
||||||||||||||||||||||||
4. |
Вычислить предел lim |
( 5 −1) 3 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
1− 2 |
||||||||||||||||||||||||||
|
→0 |
|
|
|
|
|
|||||||||||||||||||||||||
5. |
Вычислить предел lim |
|
|
3−1 |
|
||||||||||||||||||||||||||
2+ −2 |
|||||||||||||||||||||||||||||||
|
→1 |
||||||||||||||||||||||||||||||
6. |
Вычислить предел lim |
|
|
√ |
−3 |
|
. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
→3 √ +6−3 |
||||||||||||||||||||||||||||||
|
|
(√ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
7. |
Вычислить предел lim |
+2−√3)2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
→1 |
|
|
|
|
|
−1 |
||||||||||||||||||||||||
8. |
Вычислить предел lim |
|
2 ∙ (1−3 )∙ 10 |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
→0 |
|
|
|
|
|
|
|
( 4 −1)2 |
||||||||||||||||||||||
9. |
Вычислить предел. lim |
√ |
+2 |
−2. |
|||||||||||||||||||||||||||
|
→2 |
|
|
|
3−8 |
||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
10. Вычислить предел lim |
|
2−5 +2 √27 6+6 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 2− +1 |
||||||||||||||||||||||||
|
→∞ |
|
|
|
|
|
|||||||||||||||||||||||||
|
√ |
|
|
|
|
||||||||||||||||||||||||||
11. Вычислить предел lim |
+2−√3 |
. |
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
→1 |
|
(2 −2)2 |
||||||||||||||||||||||||||||
НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ ВОПРОСЫ
1. |
lim |
| | |
=? |
||
|
|
||||
|
→+0 |
|
|||
2. |
lim |
| | |
=? |
||
|
|
||||
|
→−0 |
|
|||
3.lim { } =?
→3−0
4.lim { } =?
→2+0
5.lim [ ] =?
→3+0
|
|
3 |
|
|
||
|
|
|
|
|||
6. |
Чему равен скачок функции ( ) = |
2−5+2 |
√27 6+6 |
в нуле? |
||
3 2− +1 |
||||||
|
|
|
||||
7. |
Функция ( ) непрерывна на отрезке [0;1]. Если (1) = , то lim ( ) =? |
|||||
|
|
|
|
|
→1 |
|
8. |
Функция ( ) непрерывна на отрезке [−1; 1]. Если (0) = , то lim ( ) =? |
|||||
|
|
|
|
|
→0 |
|
9.Функция ( ) непрерывна на отрезке [0;1]. Если ( ) = ( 2 − 1)/ при ≠ 0, то (0) =?
10.Функция ( ) непрерывна на отрезке [0;1]. Если ( ) = (2)/ при ≠ 0, то (0) =?
11. |
Скачок функции ( ) в точке = −1 равен двум. Если lim |
( ) = 3, то |
lim |
( ) =? |
|
→−1+0 |
→−1−0 |
||
12. |
Скачок функции ( ) в точке = 1 равен минус двум. Если |
lim ( ) = −3, то |
lim ( ) =? |
|
|
|
→1+0 |
|
→1−0 |
13. При каком А функция ( ) = {3 − 5, если ≠ 1 непрерывна в точке = 1.
, если = 1

14. |
При каком А функция ( ) = { |
+ 1, если ≠ 1 |
непрерывна в точке = 1. |
|||
3 , если = 1 |
|
|||||
|
|
+ 1, |
|
если < −1 |
|
|
15. |
При каком значении функция ( ) = { 2 − , |
|
если ≥ −1 |
непрерывна на . |
||
|
|
+ , |
|
если < 1 |
|
|
16. |
При каком значении функция ( ) = { 3 2, |
если ≥ 1 непрерывна на . |
||||
17.Чему равен скачок функции { } точке 0 = 2.
18.Чему равен скачок функции [ ] точке 0 = −3.
19.Чему равен скачок функции ( ) = |2 | в точке = 0.
20.Чему равен скачок функции ( ) = |3 | в точке = 0.
21.Чему равен скачок функции ( ) = [2х] в точке = 0.75.
22.Чему равен скачок функции ( ) = [2х] в точке = 1
23.Чему равен скачок функции ( ) = {2х} в точке = −1.4.
24.Чему равен скачок функции ( ) = {2х} в точке = −2,5.
25.Найдите приращение функции ( ) = ( − 3)2 + 4 при изменении аргумента от до + ∆ .
26.Найдите приращение функции ( ) = ( + 4)2 − 3 при изменении аргумента от до + ∆ .
27.Найдите приращение функции ( ) = 2 − 5 при изменении аргумента от 0 до .
28.Найдите приращение функции ( ) = 3 + 5 при изменении аргумента от 0 до .
29.Найдите приращение функции ( ) = 1/ при изменении аргумента от 0 до .
30.Классифицируйте точки разрыва функции
31.Классифицируйте точки разрыва функции
32.Классифицируйте точки разрыва функции
33.Классифицируйте точки разрыва функции
2 + 1, |
если < 1 |
||||||||
( ) = {1 + 2 , |
если ≥ 1, если таковые имеются. |
||||||||
3 + 1, |
если < 1 |
||||||||
( ) = {3 + 2, |
если ≥ 1, если таковые имеются. |
||||||||
|
1 |
|
, |
|
если < 1 |
||||
( ) = { −2 |
|||||||||
|
|
|
|
, если таковые имеются. |
|||||
|
2 |
|
, |
|
если ≥ 1 |
||||
|
+1 |
|
|||||||
|
|
|
|
|
|
||||
|
|
−2 |
|
|
, |
если < 0 |
|||
( ) = { +1 |
|||||||||
|
|
, если таковые имеются. |
|||||||
1 |
|
|
|
|
, |
если ≥ 0 |
|||
|
|
|
|
|
|
|
|||
|
−0.5 |
|
|||||||
|
|
2 |
|
, |
|
если < 1 |
||
|
Классифицируйте точки разрыва функции ( ) = { +1 |
|
||||||
34. |
|
|
, если таковые имеются. |
|||||
|
1 |
|
, |
|
если ≥ 1 |
|||
|
|
|
−2 |
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
, если > 0 и ≠ 1 |
|||
35. |
Классифицируйте точки разрыва функции ( ) = { −1 |
|||||||
|
|
,, если таковые имеются. |
||||||
|
2, |
|
если = 1 |
|||||
|
|
|
+2 |
, |
если ≠ −2, если таковые имеются. |
|||
36. |
Классифицируйте точки разрыва функции ( ) = { +2−1 |
|||||||
|
|
|
, |
|
если = −2 |
|||
37.В какой области непрерывна функция = ?
38.В какой области непрерывна функция = arccos(1 − )?
39.В какой области непрерывна функция = √ 2 − 4?
40.В какой области непрерывна функция = √1 + 2?
41.В какой области непрерывна функция ( ) = 2 ?
− −6
42.В какой области непрерывна функция ( ) = 2 ?
− −6
43.В какой области непрерывна функция ( ) = 21+ ?
− +6
44.Справедливо ли заключение теоремы Больцано-Коши для функции ( ) = | | на отрезке [−1; 3]?
45.Убедитесь, что для функции ( ) = 2 − 2 на отрезке [1;3] cправедлива теорема Больцано-Коши.
46.Убедитесь, что для функции ( ) = на отрезке [0; 1] cправедлива теорема Больцано-Коши.
47.Справедливо ли заключение 2-ой теоремы Больцано-Коши для функции ( ) = [ ] на отрезке [0; 2]?
48.Убедитесь в том, что для функции ( ) = 3 на отрезке [ /2; 3 /2] справедливо утверждение теоремы Вейерштрасса.
49.Убедитесь, что для функции ( ) = 2 − 2 + 2 на отрезке [0; 2] cправедлива теорема Вейерштрасса.
50.Убедитесь, что для функции ( ) = на отрезке [1; ] cправедлива теорема Вейерштрасса.
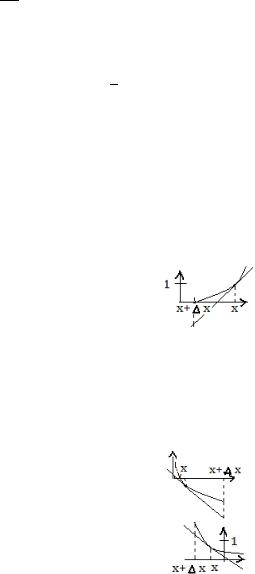
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
ВОПРОСЫ
1.Чему равна производная функции = 3 −2 ?
2.Чему равна производная функции = (2 + 3 ) 3 ?
|
Чему равна производная функции = |
3 |
|||
3. |
|
|
? |
||
2 −1 |
|||||
|
|
|
3 |
|
|
1. |
Чему равна производная функции = |
ln(2 +1) |
? |
||
|
|||||
|
|
|
5 |
||
2. |
Чему равна производная функции = exp( 2 )? |
||||
3. |
Чему равен угловой коэффициент нормали к параболе = 2 + 3 над точкой = 1? |
||||
4. |
Под каким углом график функции = пересекает ось ? |
||||
5. |
Под каким углом кривая = пересекает ось ? |
||||
6. |
Под каким углом кривая = 2 − + 3 пересекает ось ? |
||||
7. Под каким углом график функции = 2 пересекает ось ?
2
8.В какой точке касательная к параболе = 2 + 3 − 5 параллельна прямой = 4 − 3?
9.Какова разность между приращением функции ( ) = 3 − 2 и ее дифференциалом?
10.Какова разность между приращением функции ( ) = 2 и ее дифференциалом?
11.Какова разность между приращением функции ( ) = 1 и ее дифференциалом?
12.Чему равна функция ( ) и ее производная в точке 0 = 1, если уравнение нормали к графику функции над этой точкой имеет вид = −2 + 1?
13.Чему равна функция ( ) и ее производная в точке 0 = 1, если уравнение касательной к графику функции над этой точкой имеет вид = −2 + 1?
14.Чему равна функция ( ) и ее производная в точке 0 = 1, если уравнение касательной к графику функции над этой точкой имеет вид + 2 + 3 = 0?
15.Чему равна функция ( ) и ее производная в точке 0 = 1, если уравнение нормали к графику функции над этой точкой имеет вид 3 + 2 + 1 = 0?
16.Определите по графику приращение функции и дифференциал
17. Определите по графику приращение функции и дифференциал |
. |
18.Определите по графику приращение функции и дифференциал 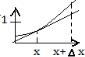 .
.
19.Определите по графику приращение функции и дифференциал 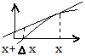 .
.
20. Определите по графику приращение функции и дифференциал |
. |
21. Определите по графику приращение функции и дифференциал |
. |
22.Определите по графику приращение функции и дифференциал 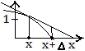 .
.
23.Определите по графику приращение функции и дифференциал  .
.
24.В каких точках функция ( ) = | | не дифференцируема
25.Где дифференцируема функция ( ) = |1 + |?
26.Где дифференцируема функция ( ) = | − 1|?
27.В каких точках функция ( ) = | | не дифференцируема?
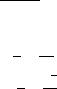
28.В каких точках функция ( ) = | 2 + 3 − 4| не дифференцируема?
29.Справедлива ли теорема Ролля для функции ( ) = | | на отрезке [−1; 1]?
30.Убедиться что теорема Ролля для функции ( ) = 3 − 2 справедлива на отрезке [0; 1].
31.Вычислив приращение функции ( ) = 2 − 2 − 3 на отрезке [1; 3], убедитесь в справедливости теоремы Лагранжа.
32.Вычислив приращение функции ( ) = 2 + 2 на отрезке [1;2], убедитесь в справедливости формулы конечных приращений Лагранжа.
33.Вычислив приращение функции ( ) = 2 + 2 на отрезке [1;2], убедитесь в справедливости формулы конечных приращений Лагранжа.
34.Вычислив приращение функции ( ) = на отрезке [1; ], убедитесь в справедливости формулы конечных приращений Лагранжа.
35.Вычислив приращения функций ( ) = , ( ) = 2 на отрезке [1; ], убедитесь в спрaведливости теоремы Коши.
36.Вычислив приращения функций ( ) = , ( ) = на отрезке [0; /2], убедитесь в спрaведливости теоремы Коши.
37.Вычислив приращения функций ( ) = 2, ( ) = 3 на отрезке [0; 1], убедитесь в справедливости теоремы Коши.
38. 2( 3 + 5 ) |
| |
=5 |
=? |
|
∆ =−0,1 |
|
|
|
|
|
|
39. 3( 4 − 7 ) |
| |
=5 |
=? |
|
∆ =−0,1 |
|
|
|
|
|
ЗАДАЧИ
1. |
Вычислить производную { = (3 + 2) |
|
= 4 |
2. |
Вычислить производную{ = (3 + 2). |
|
= 4 |
3.Вычислить приближенно arcsin(−0.1).
4.Вычислить приближенно √0,044.
5.Вычислить приближенно 0.12.
6.Вычислить приближенно (4 + 201 ).
7.Вычислить приближенно sin(6 + √243).
8.Вычислить приближенно 0.9.
9.Вычислить предел lim 2 − .
|
|
→+∞ |
||||||||
10. |
|
lim |
ln(3+ 2). |
|||||||
Вычислить предел |
|
|
|
|
|
. |
|
|||
|
|
|
|
|
||||||
|
|
→∞ |
|
|
|
|||||
11. |
Вычислить предел lim |
ln(1−2 )+2 |
. |
|||||||
|
|
|
|
|||||||
|
|
→0 |
|
|
2 |
|||||
12. |
Вычислить предел lim . |
|||||||||
|
|
→+0 |
|
|
|
|
|
|
||
13. |
Вычислить предел lim |
|
ln 2 |
. |
||||||
|
|
|
||||||||
|
|
→+0 |
3 |
|||||||
14. |
Вычислить предел |
lim |
|
|
ln 2 |
. |
||||
|
|
|
||||||||
|
|
→+∞ 3 |
||||||||
15. |
Вычислить предел lim . |
|||||||||
|
|
→+0 |
|
|
|
|
|
|
||
ИССЛЕДОВАНИЕ ФУНКЦИИ ВОПРОСЫ
1.Изобразите схематически график функции ( ) над интервалом ( , ), если на ( , ) ( ) > 0,
′( ) < 0, ′′( ) < 0.
2.Изобразите схематически график функции ( ) над интервалом ( , ), если на ( , ) ( ) < 0,
′( ) < 0, ′′( ) > 0.
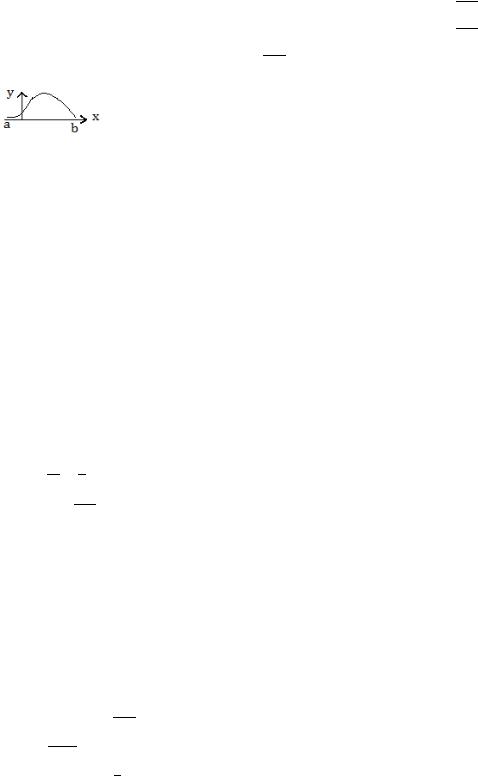
3.Изобразите схематически график функции ( ) над интервалом ( , ), если на ( , ) ( ) > 0,
′( ) > 0, ′′( ) > 0.
4.Изобразите схематически график функции ( ) над интервалом ( , ), если на ( , ) ( ) < 0,
′( ) < 0, ′′( ) < 0.
5.Напишите уравнения асимптот графика функции ( ) = 2 + 3 + −45, если таковые имеются.
6.Напишите уравнения асимптот графика функции ( ) = 3 − 2 + +45 , если таковые имеются.
7.Найдите точки перегиба функции = −23.
8.Постройте схематически график ′( ) над ( , ), если график функции ( ) имеет.вид
9.Постройте схематически график ′( ) над ( , ), если график функции ( ) имеет.вид 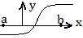 .
.
10.Постройте схематически график ′′( ) над ( , ), если график функции ( ) имеет.вид 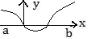
11.Постройте схематически график ′′( ) над ( , ), если график функции ( ) имеет.вид 
12.Постройте схематически график ′( ) над ( , ), если график функции ( ) имеет.вид 
13.Постройте схематически график ′′( ) над ( , ), если график функции ( ) имеет.вид 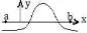
14.Постройте схематически график ′′( ) над ( , ), если график функции ( ) имеет.вид 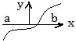 .
.
ЗАДАЧИ 1. Найти интервалы монотонности и экстремумы функции = 2 3 + 3 2 − 12 + 1
2. y = x4 − 2x2 + 3
3. y = x12 − 1x
4. y = x + x−92
5. y = (x + 3)e2x
6. = 2 − . Найти наибольшее и наименьшее значение функции
7. = 4 + 2 2 − 3 на отрезке [−2; 0] 8. = 5 − 5 4 + 5 3 + 3 на отрезке [0; 2]
9. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции = 3 − 5 2 + 3 − 1
10. = 4 − 6 3 + 12 2 + 3 11. = − 12. = 2 − 3 + −41.
13. = 1+ 2.
14. = 2( − 52).
15. Найти асимптоты графика функции = −
16. = |
−1 |
|||
|
|
. |
|
|
2+ −2 |
||||
17. = |
3 +1 |
. |
|
|
|
||||
|
2 −1 |
|||
18. = |
3 2+2 −1 |
|||
|
. |
|||
|
||||
|
+1 |
|||
19. = |
3 3+2 −1 |
|||
|
. |
|||
2+1 |
||||
ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

|
|
|
|
|
|
|
|
|
ВОПРОСЫ |
|||
1. |
Если |
(2,3) |
|
|
= 1, то с геометрической точки зрения это означает, что ... |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
2. |
Если |
(2,3) |
|
|
= −1, то с геометрической точки зрения это означает, что ... |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
3. |
Если |
(2,−3) |
= 0, то с геометрической точки зрения это означает, что ... |
|||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
4. |
Найдите частные производные функции = |
+ 1. |
||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
5. |
Если = 3 |
∙ 3 , то ′ |
, ′ =? |
|||||||||
|
|
|
2 |
|
|
|
|
|
||||
6. |
Если = |
, то ′ |
, ′ =? |
|||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
7.В каком направлении в точке ( , 1) функция = cos быстрее всего убывает?
8.В каком направлении в точке ( /2, −1) функция = cos быстрее всего возрастает?
9.Найти производную функции = 2 + 2 в точке (3,4) по направлению градиента.
10.Чему равна производная функции = 2 − 2 в точке (1,2) по направлению, перпендикулярному направлению градиента
11.Чему равна производная функции = 3 + 2 − √14 в точке (1,2) по направлению градиента.
12.Вычислите в точке (1; 2) производную по направлению оси функции = .
13.Вычислите в точке (1; 2) производную по направлению оси функции = .
14. |
( + 2 ) |
=3 |
=? |
|
| |
=4 |
|
|
∆ =−0,2 |
|
|
|
∆ =0,1 |
|
|
15. |
(2 + 3) |
=−2 |
=? |
|
| |
=−1 |
|
|
∆ =0,2 |
|
|
|
|
∆ =−0,1 |
|
16. |
(2 − 2) |
=−1 |
=? |
|
| |
=2 |
|
|
∆ =0,2 |
|
|
∆ =−0,1
17.Нарисуйте линию уровня функции = + 1 со значением = 3.
18.Нарисуйте линию уровня функции = со значением = 1.
19.Нарисуйте линию уровня функции = − 2 + 2 со значением = −3.
20.Нарисуйте линию уровня функции = 2 − со значением = 4.
21.Нарисуйте линию уровня функции = 2 + 2 + 1 со значением = 5
22.Найти стационарные точки функции = 2 − 3 + 2 + 5 − 1.
23.Найти стационарные точки функции = 2 + + 2 − + − 2.
24. Если ′′ |
= , ′′ |
= |
|
, ′′ |
= + , то имеет ли функция ( , ) в стационарной точке (1;2) |
|
|||||
|
|
|
|
|
|
локальный экстремум? Если да, то какой?
ЗАДАЧИ
1. |
= |
|
5+ 4 |
. Найти |
|
, |
|
|
|
|
|
|
|
|||
ln(3 −4 ) |
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
= ( 3cos( )). Найти |
|
, |
|
. |
|
|
|||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
3. |
= |
1 |
|
. Найти . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
√5 −3 |
|
|
|
|
|
|
|
|
|
|||||||
4. |
= |
1 |
|
|
. Найти . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||||
(3 + 4 )2 |
|
|
|
|
|
|||||||||||
5. |
Исследовать на экстремум функцию = 3 + 3 − 3 + 1. |
|||||||||||||||
6. |
Исследовать на экстремум функцию = 2 − + 2 − 2 + + 4. |
|||||||||||||||
7. |
Исследовать на экстремум функцию = 2 + + 2 − 2 − + 3. |
|||||||||||||||
8. |
Найти производную функции = |
|
в точке (−1,1) по направлению, бисектриссе 1-й |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
четверти.
9.Найдите нормаль к линии уровня функции = − 2 + 2 со значением = −2 в точке (1, −1).
10.Найти нормаль к линии уровня функции = со значением = в точке (1, ).
