Основы_акустики_Гринченко_Вовк
.pdf
(2.6) функции и производные входят линейно, что и отражено в вы- ражении “линейные дифференциальные уравнения”. В формулу (2.4) искомая функция входит нелинейно (sinθ). Разница в поведении ме- ханических систем, которые описываются линейными и нелинейными уравнениями, очень велика. Суть, причина и содержание этих урав- нений в определенной степени раскрываются в разделе 11. Но уже в данном параграфе можно четко проследить причину возникновения нелинейности. Математический маятник — это единственная из рас- сматриваемых систем, для которой написание математического соот- ношения, отражающего связь между отклонением системы от поло- жения равновесия и восстанавливающей силой, не требует предполо- жений, упрощающих и идеализирующих источник колебаний. Нели- нейность (2.4) исчезает, если предположить малость отклонений от по- ложения равновесия, аналогично тому, как это сделано при описании других систем, приведенных на рис. 2.1.
Представим функцию sinθ в виде ряда
sinθ = θ − |
θ3 |
+ |
θ5 |
−... |
(2.7) |
|
3! |
|
5! |
|
|
Если анализ задачи и требуемая точность решения позволяет пренеб- речь слагаемыми с третьей и высшими степенями θ, то sinθ ≈ θ, и уравнение (2.4), принявшее вид
lθ + gθ = 0 , |
(2.8) |
будет аналогично уравнениям для других рассмотренных систем. При этом можно сказать, что в случае малых отклонений от поло- жения равновесия движение математического маятника описыва- ется линейным дифференциальным уравнением.
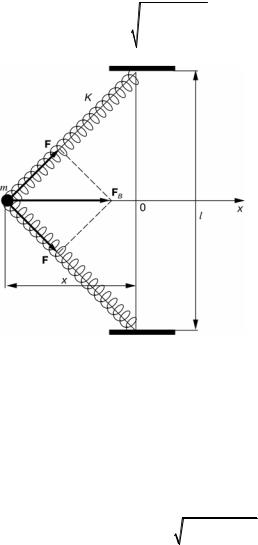
Заметим, что можно привести примеры моделей колебательных систем, которые являются нелинейными даже при малых отклонениях системы от положения равновесия. Рассмотрим, например, систему, приведенную на рис. 2.2. Здесь оба конца витой пружины зафикси- рованы на определенном расстоянии l один от другого, а масса m прикреплена к центру пружины; К — жесткость пружины. Поскольку масса двигается вдоль оси Ox, то восстанавливающая сила FB(x) равна проекции силы упругости пружины F на ось Ox. Силой тяжести, кото- рая действует на массу m, будем пренебрегать (она не вносит вклад в восстанавливающую силу).
В соответствии с рис. 2.2 деформация пружины ξ определяется соотношением: ξ = 2 (l /2)2 + x2 −l0 , где l0 — длина пружины в неде-
формированном состоянии. Тогда потенциальная энергия системы ЕП выражается соотношением
31
|
2 |
|
K |
|
l |
|
2 |
|
2 |
|
EП(ξ) = |
K ξ |
= |
2 |
|
+ x2 −l0 |
. |
||||
|
|
|
|
|
|
|||||
2 |
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.2. Пример нелинейной колебательной системы
(Напомним, что потенциальная энергия ЕП пружины определяется работой
ξ
против силы упругости, т.е. EП = ∫ K ξdξ = K ξ2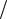 
2 .) Учитывая связь между
0
потенциальной энергией и восстанавливающей силой, действующей вдоль оси Ох, находим выражение для этой силы:
|
|
dEП |
|
|
l0 |
1 |
|
|
|
|
|
(x ) = − |
|
|
|
|
(2.9) |
||||
F |
|
= −4Kx 1 |
− |
|
|
|
|
. |
||
|
|
|
|
|||||||
В |
|
dx |
|
|
l |
|
1 + (2x /l )2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Разложим это выражение в ряд в окрестности малых значений вели-
чины (x/l) < 1:
F |
(x ) = −4K (l −l |
|
) x |
− 8Kl |
|
|
|
|
3 |
− 3 |
|
|
5 |
|
(2.10) |
0 |
0 |
x |
|
x |
+... . |
||||||||||
В |
|
l |
|
|
l |
|
|
|
|
l |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если х << l, то, конечно, можно пренебречь высокими степенями x/l, и считать силу линейной относительно х. Тем не менее, если длина не- деформированной пружины l0 равна расстоянию l между крепления- ми, то линейный член исчезает, и даже для малой величины x восста-
32
навливающая сила FВ (x ) ≈ −8Kx3 /l2 пропорциональна кубу смеще-
ния.
Следует сказать, что наличие линейной зависимости восстанавли- вающей силы при малых колебаниях системы является, как говорят, типичной в природе. Поэтому в начале будем рассматривать именно такие колебания. После деления (2.3), (2.5), (2.6) и (2.8) на коэффици- ент при второй производной становится очевидным, что для всех слу- чаев коэффициент при обобщенной координате имеет размерность: единица, деленная на секунду в квадрате. Это дает возможность сде- лать вывод о том, что закономерности изменения во времени обоб- щенных координат для всех рассматриваемых систем (рис. 2.1) пол- ностью идентичны, и для их изучения можно ввести некоторую новую математическую модель, которая охватывает все рассмотренные час- тичные физические модели. Дифференциальное уравнение этой ма- тематической модели имеет вид
ξ + ω02ξ = 0, |
(2.11) |
где размерность ω0, с–1.
Понятно, что дальнейшее движение системы определяется ее на- чальным состоянием, или, как говорят, начальными условиями, кото- рые записывают для некоторого момента времени t, пусть это будет t = 0. Начальные условия, очевидно, обусловлены заданием начальных
обобщенных координат смещения и скорости: |
|
ξ(0) = ξ0, ξ(0) = υ0. |
(2.12) |
Такая математическая модель получила название гармоничного ос- циллятора (от латинского слова oscillo — колеблюсь). Суть этого на- звания становится понятной при анализе решения уравнения (2.11).
Задание именно двух начальных условий (2.12) легко понять с фи- зической точки зрения. Предположим мы хотим знать состояние ос- циллятора в некоторый момент времени. Для этого нам недостаточно знать смещение ξ, ведь в дальнейшем оно может, как увеличиваться, так и уменьшаться. Необходимо также знать скорость осциллятора ξ
в тот же момент времени. Таким образом, поведение осциллятора
полностью описывается эволюцией во времени двух величин ξ(t) и
ξ(t ).
Пример 2.1. Начальные условия для математического маятника таковы: θ(0) = θ0 , θ(0) = 0 . Определить максимальное значение угла
θ0 при условии учета только линейного члена в ряде (2.7). Считать, что второй член ряда (2.7) меньше первого минимум в десять раз.
33
Решение. Согласно условию θ30 /(6θ0 ) = 0,1 ; отсюда, максимальный угол отклонения маятника равен θ0 ≈ 44 .
2.1.3. Гармонический осциллятор
Уравнение (2.11) описывает закономерности движения, общие для многих электрических и механических систем. Для кон- кретного изучения этих закономерностей необходимо найти решение этого уравнения и привести его в соответствие с заданными началь- ными условиями. В математике существует специальный раздел, по- священный теории дифференциальных уравнений, который содер- жит в себе и разработку методов их решения. Для тех уравнений, ко- торые встречаются в данном разделе, решения могут быть получены на основе довольно простых и наглядных соображений.
Уравнение (2.11) — это некоторое алгебраическое соотношение, которое связывает значение функции и ее второй производной в лю- бой момент времени. Поэтому решением этого уравнения может быть функция, которая не изменяет своего вида вследствие двукратного дифференцирования или, как говорят, является инвариантной (от латинского слова invarians — неизменный) относительно операции двукратного дифференцирования. Функции такого типа хорошо из- вестны из математического анализа. Например, функция
y(t) = A exp(αt) |
(2.13) |
имеет такое свойство относительно операции дифференцирования любого порядка n :
y(n)(t) = Aαn exp(αt).
Бесспорно, такую функцию y(t) можно использовать как пробную для получения решения (2.11). Хорошо известно также, что тригоно- метрические функции имеют указанное свойство относительно опера- ции дифференцирования любого парного порядка:
y1(t) = Acos(αt), y2(t) = Bsin(αt); (2.14)
y1(2n )(t) = A (−1)n α2ncos(αt), y2(2n )(t) = B (−1)n α2nsin(αt).
Таким образом, и тригонометрические функции могут быть ис- пользованы как пробные, при стремлении найти решение (2.11). Рас- смотрим процедуру получения решения с использованием функции (2.13), т.е. предположим, что искомая функция имеет вид:
ξ(t) = A exp(αt ). |
(2.15) |
34
В этом выражении есть две произвольных величины — А и α, которые следует определить так, чтобы искомая функция удовлетворяла урав- нению (2.11). Подставляя выражение (2.15) в (2.11), получаем
A α2 |
+ ω2 |
exp(αt ) = 0. |
(2.16) |
|
0 |
|
|
Видно, что постоянная А не определяется из полученного соотноше- ния. Что касается постоянной α, то уравнение не может быть удовле- творено при любом действительном значении величины α. Но, допус- кая возможность комплексных величин α, в частности, в данном слу- чае чисто мнимых величин, легко убедиться, что (2.15) есть решение (2.11) только в случае, если α принимает два значения:
α1 = iω0, α2 = −iω0 |
.(2.17) |
Таким образом, для исходного уравнения (2.11) найдено два решения:
ξ1(t) = A exp(iω0t ), ξ2(t) = B exp(−iω0t ). |
(2.18) |
Поскольку само уравнение никаких ограничений на значение множи- теля при экспоненте не накладывает, то, конечно, в разных решениях эти множители можно брать отличными друг от друга.
Исходное уравнение (2.11) описывает поведение реальных физи- ческих систем. По своему физическому смыслу искомая функция ξ(t)
есть величина, которая измеряется. В связи с этим комплексная форма решения, на первый взгляд, не пригодна. Но для уравнения с действительными коэффициентами решением является отдельно взятая действительная и мнимая части комплексного решения. По- этому ясно, что вместо (2.18) в дальнейшем можно использовать реше- ния вида
ξ1 (t ) = a cos (ω0t ), ξ2 (t ) = b sin(ω0t ), |
(2.19) |
где a и b — произвольные действительные постоянные. Такая лег- кость перехода от комплексных (не физических) к действительным (измеряемым) величинам обуславливает очень широкое использование в акустике комплексных изображений для искомых величин. При этом существенно упрощаются промежуточные выкладки. Это позво- ляет широко использовать комплексные функции при изложении ма- териала.
Выражения (2.19) представляют собой два конкретные частные решения исходного уравнения. Вследствие линейности уравнения его решением будет любая линейная комбинация частных решений, т.е.
ξ(t ) = a cos (ω0t )+b sin(ω0t ). |
(2.20) |
35
В теории дифференциальных уравнений доказывается, что любое ча- стное решение уравнения (2.11) может быть получено из выражения (2.20) выбором конкретных значений величин a и b. Именно поэтому его называют общим решением дифференциального уравнения (2.11).
С физической точки зрения такое математическое утверждение ука- зывает на то, что выбором значений a и b можно описать движение механической или электрической системы при любых начальных ус- ловиях. В справедливости этого легко убедиться.
Если в (2.20) задать начальные условия для ξ, как в (2.12), то мож- но легко найти значение постоянных a и b, и решение будет иметь вид
|
|
|
|
ξ(t) = ξ |
0 |
cos(ω t) + |
υ0 |
sin(ω t). |
(2.21) |
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
ω0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Этому решению можно придать более удобное представление |
|
||||||||||||
|
|
|
|
|
ξ(t) = A cos(ω0t + ϕ0 ), |
(2.22) |
|||||||
где A = ξ2 |
|
υ |
2 |
|
|
|
ξ |
0 , sinϕ = − |
υ |
|
|||
+ |
0 |
|
, cosϕ |
|
= |
|
0 |
. |
|
||||
|
|
|
|
||||||||||
0 |
|
ω0 |
0 |
|
A |
0 |
|
ω0A |
|
||||
Соответственно скорость осциллятора будет иметь вид |
|
||||||||||||
|
|
|
|
ξ(t) = −ω0Asin(ω0t + ϕ0 ). |
(2.23) |
||||||||
Таким образом, решение уравнения (2.11), описывающего поведе- ние гармоничного осциллятора, получено. Решена достаточно простая задача динамики — известно состояние системы в определенный мо- мент времени, если известны начальные условия ее движения.
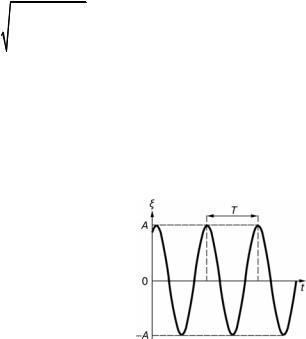
Рис. 2.3. График гармонического колебания
Колебания, которые определяются функцией синуса или косинуса, называются гармоничными (от греческого слова αρμονιχος — созвуч-
ный). Итак, движение системы (2.11) — это простое гармоничное ко-
36
лебание (рис. 2.3). В теории колебаний, как части физической акусти- ки, почти не интересуются такими локальными вопросами: где в дан- ный момент находится система. Более важным вопросом является определение интегральных характеристик движения колебаний сис- темы.
В решении (2.22) такими интегральными характеристиками есть три величины — амплитуда колебаний (А), угловая частота (ω0) и на- чальная фаза (ϕ0). Функция ϕ(t ) = ω0t + ϕ0 называется фазой колеба-
ния. В соответствии с выражением (2.22) начальная фаза ϕ0 опреде- ляет сдвиг фазы данного колебания относительно колебания, которое началось при нулевой начальной скорости (υ0 = 0). Частоту ω0 назы-
вают собственной частотой осциллятора.
Фаза колебаний ϕ(t ) = ω0t + ϕ0 возрастает неограниченно со временем.
Тем не менее, поскольку функции синуса и косинуса являются периодиче-
скими функциями с периодом 2π, то две фазы, которые различаются на 2π, отвечают одному и потому же физическому состоянию колеба- тельной системы. Поэтому часто, для удобства, изменение фазы опре- деляют от 0 до 2π. Поскольку производная ϕ′(t ) = ω0 , то понятно, что
угловая частота ω 0 определяет скорость изменения фазы колебаний со временем (2.22).
Движение в соответствии с (2.22) является периодическим, т.е. система возвращается в любое из возможных состояние после некото- рого промежутка времени Т (рис. 2.3). Величина этого временного па- раметра, который называют периодом колебаний, определяется из равенства, вытекающего из свойств тригонометрических функций:
ω0T = 2π, с–1, |
T = |
2π |
, с. |
(2.24) |
|
||||
|
|
ω0 |
|
|
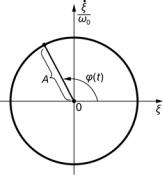
Рис. 2.4. Пример гармонического колебания на плоскости переменных ξ и
ξ
ω0
37
Поскольку переменные ξ(t) и ξ(t ) полностью описывают поведение осциллятора, то их можно определить как координаты декартовой системы координат (ξ,ξ). Тогда с изменением времени точка на плос-
кости (ξ,ξ) вычерчивает некоторую линию. Понятно, что, когда коле-
бания периодические, то кривая будет замкнутой. Имея выражения (2.22) и (2.23), нетрудно получить уравнения этой кривой:
ξ2 + ξ2 /ω20 = A2. Если в качестве координат приняты переменные ξ и ξ
ω0 , то имеем уравнение окружности (рис. 2.4). Как видим, величи- ны А і ϕ(t) есть не что иное, как полярные координаты точки на плос- кости (ξ,ξ). Эта точка вращается против часовой стрелки с угловой
скоростью ω0 (ведь ϕ′(t ) = ω0 ), так что за один период колебаний T она
выполняет один оборот, и фаза ϕ(t) возрастает на 2π.
Согласно определению угловая частота ω0 = 2π/Т выражается в ра- дианах за секунду. Поскольку радиан есть величина безразмерная, то размерность ω0, с–1, она определяет число колебаний системы за 2π секунд. Вместе с угловой частотой ω0 при описании колебательных процессов используют такую характеристику, как число колебаний за одну секунду — f0. Частота f0 связана с угловой частотой ω0 равенст- вом f0 =1/T = ω0 /(2π), Гц. Единица частоты f0 — герц, т.е. частота
процесса, в котором одно колебание происходит за одну секунду. Ко- нечно, если это не вызывает недоразумений, ω и f имеют одинаковое название — частота.
Перепишем выражение для скорости гармонического осциллятора
(2.23) в виде ξ(t ) = −ω0Asin(ω0t + ϕ0 ) = ω0Acos (ω0t + ϕ0 + π/2). О такой записи можно говорить, что скорость ξ(t ) опережает по фазе измене- ние координаты ξ(t) на величину π/2. Дифференцируя вторично, на-
ходим |
ускорение |
ξ(t ) = −ω2Acos (ω t + ϕ |
) = ω2Acos (ω t + ϕ + π). |
||||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
Ускорения ξ(t ) изменяется за тем же законом, что и координата ξ(t)
осциллятора, но опережает ее по фазе на π. Начертите графики зависимости ξ, ξ, ξ от времени t и подумайте самостоятельно над их фазовыми соотношениями.
Записанные выше формулы для ξ, ξ, ξ устанавливают связь меж-
ду амплитудами колебаний A, скорости Аυ и ускорение Aa : Aυ = ω0A,
Aa = ω20A = ω0Aυ.
Пример 2.2. На платформе, которая выполняет гармонические колебания с частотой 5 Гц в вертикальном направлении, размещен
38
груз. Показать, что груз потеряет контакт с платформой, когда ее смещение превысит 0,01 м.
Решение. Груз потеряет контакт с платформой, когда ускорение платформы и ускорение силы тяготения g будут иметь одинаковое направление, а ускорение платформы будет больше, чем g. Такие условия могут быть реализованы, когда платформа находится в самом
верхнем положении при amax = ω20A > g. Подставив численные
значения величин, получим очевидное неравенство: π2 > g.
В соответствии с уравнением (2.11) квадрат собственной частоты ω0 входит как коэффициент при обобщенной координате. Поэтому построение уравнения движения системы позволяет сразу определить частоту ω0. Проиллюстрируем этот важный результат на таком при- мере.
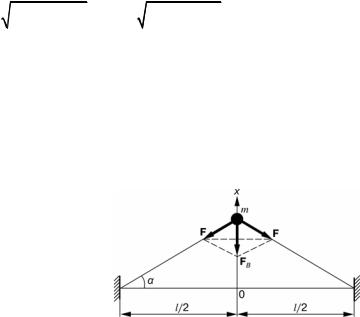
Пример 2.3. Рассмотрим малые колебания (х << l) массы m, поме- щенной посередине безмассовой струны, натянутой с силой F (рис. 2.5). Положение равновесия соответствует координате x = 0. Оп- ределить собственную частоту колебаний массы m.
В начале сделаем важное замечание относительно малости колеба- ний. В процессе колебаний сила упругости F будет изменяться на ве- личину, которая пропорциональна удлинению струны
2 |
+ x |
2 |
|
1 |
+ (2x |
2 |
|
. Разложим функцию |
l(x) в ряд |
l = 2 (l /2) |
|
−l = l |
/l ) |
−1 |
|||||
|
|
|
|
|
|
|
|
|
|
по степеням |
х/l: |
l = l (1 |
+ 0,5(2x /l )2 + …−1). Поскольку х/l << 1, то |
||||||
имеем приближенное равенство l ≈ 2l (x /l )2 , т.е. изменение натяже-
ния струны при колебании массы m есть величина второго порядка малости относительно величины отклонения x/l массы m от положе- ния равновесия. Это дает основание считать силу натяжения F в про- цессе колебаний постоянной.
Рис. 2.5. Колебательная система
Решение. Согласно рис. 2.5, восстанавливающая сила FB, которая обу- славливает движение массы вдоль осы Ох, равняется проекции силы
39
натяжения F на ось Ох: FВ = −2F sinα. Эта формула устанавливает
нелинейную связь между восстанавливающей силой FB и отклонением массы m от положения равновесия (угол α является функцией коор- динаты x), что приводит к нелинейному уравнению движения. Но,
учитывая малость колебаний (угол |
α << 1), можно |
считать, |
что |
sin α ≈ tgα = 2x l . Тогда уравнение |
движения будет |
иметь |
вид |
x + 4Fx /(ml) = 0. Отсюда искомая частота собственных колебаний сис- темы ω0 будет равна ω0 = 4F /(ml ). Как видим, ω20 пропорциональна
силе натяжения струны F и обратно пропорциональна массе m и длине струны l.
Завершая описание свободных колебаний гармонического осцил- лятора, нужно обратить внимание на следующее. Из трех указанных характеристик две — амплитуда А и фазовый сдвиг ϕ0 — зависят от начальных условий, в то время, как третья характеристика — частота ω0 — не зависит от этих условий. Частота и период колебаний осцил- лятора определяются лишь внутренними физическими свойствами системы и не зависят от того, как именно система была приведена в движение. Поэтому при решении вопроса о быстром или медленном влиянии на колебательную систему в течение временного масштаба нужно выбирать именно период собственных колебаний.
Для большинства колебательных процессов, разных по своей при- роде, характерным есть то, что при малых возмущениях от положения равновесия возникает простое гармоническое движение. Конечно, гармонические колебания могут выполнять не только малые тела, но и тела достаточно значительных размеров, например, мосты под дейст- вием порывов ветра. Тем не менее, для нас особенно важным есть то, что природа малых колебаний тесно связана с природой большинства источников звука. Это мы будем подчеркивать при изучении приро- ды звуковых волн. Но уже сейчас, принимая во внимание малость амплитуды колебаний источников звука, которые нас интересуют, мы понимаем, что частоты звуковых волн, которые они излучают, не за- висят от амплитуды колебаний источника. Именно это наблюдается в большинстве случаев, когда речь идет о звуках, которые мы слышим в окружающей среде.
2.2. Осциллятор при наличии демпфирования
2.2.1. Свободные колебания
Простейшие колебательные системы в первом параграфе данного раздела рассматривались со слишком сильным абстрагирова- нием от свойств реальных систем. При наблюдении за любой реальной
40