Основы_акустики_Гринченко_Вовк
.pdf
Для первой моды, которая имеет наименьшую собственную часто- ту, все осцилляторы колеблются в фазе. Для второй моды осцилляторы разделяются на две группы, колебания которых происходят в проти- вофазе. Для третьей моды таких групп три, и так далее. В последней моде (на рис. 2.28 — это j = N = 5) соседние шарики на струне колеб- лются в противофазе, поэтому при целых значениях j > N в формулах (2.130) и (2.131) не возникает новых типов колебаний. Итак, в систе- ме (рис. 2.25) существует N нормальных колебаний, что совпадает с числом степеней свободы. Понятно, что это утверждение имеет общий характер и не зависит от конкретного строения цепочки.
В конце раздела отметим, что на практике часто необходимо ис- следовать колебания в системах с большим числом степеней свободы. Аналитическое исследование такой ситуации очень сложное. Для по- строения решения этой важной и сложной задачи вычислительной алгебры в последние годы приложены значительных усилий. Были разработаны алгебраические алгоритмы и на их основе созданы эф- фективные программы для ЭВМ, которые позволяют практически ис- следовать системы с большим числом степеней свободы.
2.9. Задачи
2.1. Груз закрепили на нижнем конце вертикальной пру- жины и начали постепенно опускать его вниз, пока он не остановил- ся. Пружина при этом растянулась на величину x. Найдите частоту собственных колебаний груза ω 0.
Ответ: ω0 = g 
x .
2.2. Тело массой m , подвешенное на пружине, колеблется так, что наибольшее значение скорости равно υ0 , а наибольшее отклонение от положения равновесия равно x0. Найдите жесткость пружины K.
Ответ: K = mυ20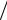 
x02 .
2.3. Круглое деревянное бревно (радиусом 0,1м) с грузом на одном конце плавает в воде вертикально. Если на верхний конец бревна на- давить и отпустить, то она будет осуществлять колебание с периодом 4 с. Определить массу бревна с грузом?
Ответ: m ≈ 124 кг.
2.4. Пуля массой m, летящая со скоростью υ , попадает в тело мас- сой M, какое связано со стеной пружиной жесткости K, и застревает в нем. Приняв момент попадания пули за начало отсчета времени, най- дите зависимость скорости и координаты тела от времени.
91
Ответ: x(t) = |
mυ |
cos(ω t), x(t) = |
mυ |
sin(ω t), ω = |
K |
. |
|
|
M +m |
0 |
K(M +m) |
0 |
0 |
M +m |
|
|
|
|
|
||||
2.5. Масса, которая свободно колеблется на пружине, за промежу- ток времени 0,01 с сместилась с расстояния 0,5 см от положения рав- новесия на наибольшее расстояние, которое равняется 1 см. Какой период колебаний?
Ответ: T = 0,06 c.
2.6. В момент времени t0 координата массы, которая выполняет гармонические колебания с частотой ω, равна x0, а скорость — υ0 . Покажите, что зависимость координаты массы от времени можно за- писать в виде:
x(t) = x |
0 |
cos ω(t |
−t |
0 |
) + |
υ0 sin ω(t −t |
0 |
) . |
|
|
|
||||
|
|
|
|
|
|
ω |
|
|
|
|
|
||||
2.7. Потенциальная |
|
энергия |
|
частицы |
массой |
m |
равна |
||||||||
|
|
a |
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
U = −2b |
− |
|
|
, где a и b — положительные постоянные, х — коор- |
|||||||||||
|
2 |
||||||||||||||
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
дината частицы. Нарисуйте график этой зависимости; определите значение координаты, которая определяет положение равновесия; найдите частоту малых собственных колебаний частицы.
Ответ: а; 2b/(ma2 ) .
2.8. Амплитуда затухающих колебаний маятника за две минуты уменьшилась в два раза. Определите коэффициент затухания.
Ответ: 5,78 10–3 с–1.
2.9. Логарифмический декремент затухающих колебаний равен 0,01. Определите количество периодов колебаний маятника, после ко- торых его амплитуда уменьшиться в три раза.
Ответ: 110.
2.10. Маятник длиной 5 м выполняет малые колебания так, что их амплитуда уменьшается в два раза за 100 периодов. Найдите доброт- ность колебаний, логарифмический декремент и коэффициент зату- хания.
Ответ: 455; 6,9 10–3; 1,5 10–3 с–1.
2.11. Собственная частота колебаний системы равняется 500 Гц. Определите частоту затухающих колебаний этой системы, если резо- нансная частота по смещению равняется 499 Гц.
Ответ: 499,5 Гц.
92
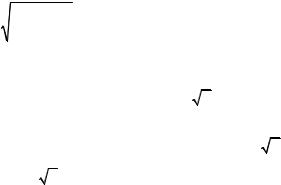
2.12. Убедитесь в том, что энергия, которая тратится за один пе- риод колебаний из-за наличия силы трения Rx , равна πRωxмакс2 , где
ω— угловая частота колебаний.
2.13.Найдите разность фаз между смещением и внешней силой на резонансе смещения, если собственная частота колебаний системы равна 50 с–1, а коэффициент затухания — 5,2 с–1.
Ответ: 840.
2.14. Колебательная система состоит из массы 0,2 кг и пружины с коэффициентом жесткости 19,6 Н/м. На массу действует внешняя сила с угловой частотой ω = 14 с–1 и сила трения Fт = −49x H . Опреде-
лите сдвиг фазы между вынужденными колебаниями и внешней си- лой.
Ответ: 91 38′.
2.15. Масса m закреплена на струне на расстоянии a от ее конца; длина струны l, а сила натяжения F. Масса выполняет малые попе- речные колебания. Определите частоту собственных колебаний массы (массой струны пренебрегать). Для какого расстояния а эта частота будет минимальной.
Ответ: |
Fl |
; |
l |
. |
|
m(l −a)a |
2 |
||||
|
|
|
2.16. Два тела с одинаковой массой (рис. 2.29) колеблются в вер- тикальном направлении. Покажите, что частоты нормальных колеба-
ний определяются так: ω2± = (3 ± 5 )K / (2m) и что отношение ампли- туды смещения верхнего тела к амплитуде смещения нижнего тела равно в случае медленных колебаний: ( 5 −1)/2; в случае быстрых
колебаний ( 5 +1)/2 .
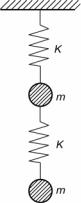Рис. 2.29. К задаче 2.16
93
2.17. Сила F (t ) = F0 cos (ωt ) действует на тело массой M (рис. 2.30), которое присоединено к телу массой m пружиной жесткости K. Покажите, что тело массой M недвижно, если ω2 = K /m ; определите амплитуду колебаний тела массой m.
Ответ: F0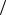 
K .
Рис. 2.30. К задаче 2.17
2.18. Исследуйте систему (рис. 2.31, а): на струне (массой струны пренебречь) закреплены два тела массой m каждое. Натяжение стру- ны F считать постоянным. Тела осуществляют малые колебания в вертикальной плоскости. Определите нормальные частоты системы. Начертите графики смещения (с течением времени) каждой из двух
масс, если |
начальные условия y1 (0) = a, y2(0) = y1(0) = y2(0) = 0 |
(рис. 2.31, б). |
3F /(ml ); ω+ = 3F /(ml ). |
Ответ: ω− = |
Рис. 2.31. К задаче 2.18
2.19. Для системы, изображенной на рис. 2.31, а, построить гра- фики смещения для каждой из двух масс, если y1 (0) = a, y2(0) = 0,5a ,
y1(0) = y2(0) = 0 .
2.20. Три шарика размещены вдоль прямой линии и соединены между собой пружинами с коэффициентом жесткости К, причем крайние шарики имеют массу m, а средний — 2m. Найдите собствен- ные моды колебаний такой системы.
Ответ: |
ω2 |
= 0, [1,1,1]; |
ω2 |
= |
k |
, [1,0,−1]; |
ω2 |
= 2k , [1,−1,−1]. |
|
||||||||
|
1 |
|
2 |
m |
3 |
m |
||
|
|
|
|
|
||||
94
Р А З Д Е Л 3
КОЛЕБАНИЕ И ВОЛНЫ В СИСТЕМАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Смотрю на волны; их неверных линий Не угадав, смущен их вечной меной… Приходят волны к нам из дали синей, Взлетают в брызгах, умирают пеной.
В.Я. Брюсов*
3.1. Переход к сплошной одномерной среде в цепочке связанных осцилляторов
Во втором разделе закономерности колебательных движе- ний рассматривались в рамках довольно грубых модельных представ- лений. Элементами колебательных систем были такие объекты, как абсолютно твердое тело с определенной массой, и идеальная пружи- на, масса которой не учитывалась. Можно констатировать, что такие модели являются значительным упрощением физических представле- ний о строении материи, и искать в этом основу для построения но- вых, более сложных моделей. Тем не менее, такой стимул, хотя и обоснованный, но не единственный. Более существенным стимулом к развитию теории колебаний было то, что результаты, полученные в рамках простейших моделей, часто не отвечали результатам опыта.
Именно в связи с требованием согласования результатов наблюде- ния и расчета формировались глубокие модельные представления о колебательных системах с распределенными параметрами или о
сплошной среде.
Представлению об атомном строении вещества в теории колеба- ний отвечают модельные представления о системах с большим, но конечным числом степеней свободы. В рамках таких представлений, возможно предусмотреть поведение системы в очень широком диапа- зоне изменения параметров внешних воздействий. Однако трудности анализа систем, которые содержат в себе 1025 атомов, слишком вели-
* Брюсов Валерий Яковлевич (1873—1924) — российский писатель.
95
ки. Упрощение этой сложной задачи возможно за счет введения представления о сплошной среде, в рамках которой, абстрагируясь от атомного строения вещества, будем говорить, что плотность и упру- гость в среде есть непрерывные функции пространственных коорди- нат. Характеризуя такой подход, который реализовал Дебай в 1912 г. при анализе теплоемкости кристаллов, Мандельштам отметил, что “он сделал, очевидно, неправильную, но гениальную вещь” [32, с. 294].
Проиллюстрируем переход от дискретной системы к модели сплошной среды на примере цепочки идентичных осцилляторов (рис. 2.25). Предположим, что пространственный период волнового движе- ния в дискретной цепочке намного больший, чем расстояние между шариками. В этом случае, возможно осуществить переход от дис- кретной пространственной координаты к непрерывной, выполнив при этом такие замены:
yn (t) → y(x,t),
y |
(t) → y((x +a),t) = y(x,t) + ∂y(x,t)a + 1 |
∂2y(x,t)a2 |
+..., |
|
n +1 |
∂x |
2 |
∂x2 |
|
|
|
|||
y |
(t) → y((x −a),t) = y(x,t) − ∂y(x,t)a + 1 |
∂2y(x,t)a2 |
−... . |
|
n −1 |
∂x |
2 |
∂x2 |
|
|
|
|||
Используя эти замены в уравнении (2.124) и отбрасывая малые вели- чины, получаем уравнение в частных производных
1 ∂2y |
= |
∂2y |
|
υ2 = |
Fa |
|
|
|
∂t2 |
∂x2 |
, |
m . |
(3.1) |
||
υ2 |
|||||||
Ниже будет показано, что любая одномерная волна может быть описана с помощью решения уравнения (3.1), где υ = const и имеет размерность скорости. Интересным есть комментарий Мандельштама в связи с таким переходом от дискретной системы к непрерывной [32, с. 339]: в исходном уравнении (2.124) функция y “…определена лишь для дискретных точек, а следовательно, у нее нет производных по x ! Дифференцирование по x — очень сомнительное средство, хотя и дает верный результат… Тем не менее в физике везде приходится де- лать такие вещи”.
Следует понимать, что упрощения не бывают “без проблем”. Вводя упрощенные представления о сплошной среде, мы, конечно, ограни- чиваем область применения таких модельных изображений. Они ос- таются справедливыми лишь для тех движений реальных тел, где
Дебай (Debye) Петер Йозеф Вильгельм (1884—1966) — голландский физик, лауреат Нобелевской премии (1936).
96
можно выделить элементы с довольно большим числом атомов, кото- рые двигаются практически одинаково. (К таким элементам можно применять законы механики.) Внешние влияния при этом не должны быть очень высокочастотными, и на их пространственную изменяе- мость тоже накладываются определенные ограничения.
3.2. Модель струны.
Уравнение движения элемента струны
В рамках представлений о сплошной среде можно построить большое количество моделей колебательных систем разной степени сложности. Начнем с простейшей одномерной модели — модели стру- ны. Суть модельных представлений легко понять при сравнении ре- альной и идеальной струн. Реальная струна всегда имеет какую-то конечную толщину. Если рассматривать относительно низкочастот- ные движения струны, то можно сказать, что все точки ее поперечно- го сечения двигаются одинаково. Поэтому модельная струна считает- ся бесконечно тонкой и имеет такую характеристику, как линейная плотность. Если известна плотность ρ0 материала струны и площадь поперечного перереза S, то линейная плотность ρ = ρ0S, кг/м.
Рис. 3.1. Элемент идеально гибкой струны
Здесь можно сказать, что, формируя модельные представления о струне, мы используем, в сущности, те же абстракции, что и при вве- дении понятия материальной точки, но не по трем, а лишь по двум пространственным измерениям.
Реальная струна всегда имеет определенную изгибную жесткость, т.е. некоторую способность оказывать сопротивление изгибу. Однако способность реальной струны восстанавливать форму обеспечивается не изгибной жесткостью, а натяжением F.
Итак, модельная струна — это идеально гибкая бесконечно тонкая нить, которая характеризуется двумя физическими параметрами: линейной плотностью ρ и натяжением F. Такая модельная струна, как
97
и реальная струна, при отклонении от положения равновесия стре- мится вернуться к нему. Наличие инерционности и упругости и обу- словливают возникновение колебаний.
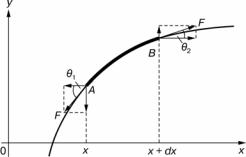
Для описания колебаний струны введем декартову систему коор- динат xOy (рис. 3.1). Пусть в состоянии покоя струна размещена вдоль оси Ox. На рис. 3.1 изображен элемент струны в состоянии от- клонения от положения равновесия. Для характеристики отклонения используем функцию y(x, t), которая определяет смещение точек струны в направлении, перпендикулярном равновесному состоянию, т.е. вдоль оси Oy. При этом предполагаем, что все точки струны после отклонения находятся в одной плоскости. Физически ясно, что после отклонения элемента струны из равновесного состояния в нем изме- няются линейная плотность и натяжение. Тем не менее, будем рас- сматривать лишь такие движения струны, при которых эти измене- ния незначительны, и ими можно пренебречь.
Получим уравнение движения выделенного элемента струны. При этом для общности будем предполагать, что, кроме сил, связанных с натяжением F, на выделенный элемент могут действовать силы со- противления и некоторые внешние вынуждающие силы. Для двух по- следних сил принимаем уже известные модели — силы сопротивления задаются своей плотностью, т.е. силой на единицу длины −R∂y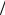
∂t , а
плотность вынуждающих сил задается некоторой функцией g(x,t), ко- торая не зависит от характера движения струны. Каждая из этих сил направлена вдоль оси Oy. Считается, что силы сопротивления про- порциональны скорости, а коэффициент пропорциональности R – по- стоянная величина.
Теперь можно записать уравнение движения элемента струны. Это, в сущности, соотношение второго закона Ньютона, взятого в проекции на ось Oy (см. рис. 3.1):
ρdx ∂2y = −R |
∂y dx + g(x,t)dx + F sinθ |
− F sin θ . |
(3.2) |
|
∂t2 |
∂t |
2 |
1 |
|
|
|
|
||
Для получения уравнения, которое имеет лишь одну неизвестную функ- цию y(x,t) , необходимо выразить через нее синусы углов θ1 и θ2. С
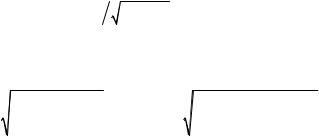
учетом соотношения sin θ = tgθ |
1 + tg2θ в соответствии с геометриче- |
||||||||
ским содержанием производной находим: |
|
|
|
|
|||||
|
|
∂y (x,t) |
|
|
∂y (x + dx,t) |
|
|||
sin θ1 = |
|
∂x |
|
, sinθ2 = |
|
∂x |
|
. |
(3.3) |
|
|
|
|
|
|
||||
1 |
∂y |
2 |
|
|
∂y |
2 |
|
||
+ |
(x,t) |
|
|
1 + |
(x + dx,t) |
|
|||
|
|
∂x |
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
98 |
Эти довольно сложные выражения пригодны для любых отклоне- ний струны от положения равновесия. В дальнейшем ограничимся малыми отклонениями, при которых профиль струны есть достаточно гладкий, т.е. углы θ (x), образованные между направлением касатель- ной в любой точке профиля струны и осью Ox, настолько малы, что можно пренебречь квадратами производных от y по сравнению с
единицей. Тогда выражение
ρdx ∂2y = −R ∂y dx + ∂t2 ∂t
(3.2) приобретает вид: |
|
|
|
||
|
∂y |
(x + dx,t) − |
∂y |
|
(3.4) |
g(x,t)dx + F |
∂x |
∂x |
(x,t) . |
||
|
|
|
|
||
Используя правило разложения в ряд Тейлора с точностью до величин второго порядка малости по dx, записываем
∂y |
(x + dx,t) = |
∂y (x,t) + ∂2y (x,t)dx +... |
(3.5) |
|
∂x |
|
∂x |
∂x2 |
|
С учетом (3.5) уравнение (3.4) приобретает вид |
|
|||
|
ρ ∂2y = F |
∂2y |
− R ∂y + g(x,t). |
(3.6) |
|
∂t2 |
∂x2 |
∂x |
|
Это и есть искомое уравнение неизвестной функции y (x, t), кото- рое описывает движение струны. В отличие от рассмотренных рань- ше, это уравнение является уравнением в частных производных. Именно в этом отразился тот факт, что рассматривается движение системы с распределенными параметрами.
Вместе с поперечным смещением частичек струны в ней возмож- но и продольное смещение частичек. Действительно, как видно из рис. 3.1, проекции силы натяжения в точках A и B на ось Ox (соот- ветственно F cos θ1 и F cos θ2 ) не равны между собой. Это должны
привести к деформации участка AB вдоль оси Ox, что было бы при- чиной возникновения так называемых продольных волн. Но мы рас- сматриваем малые колебания, для которых характерна малость углов
θ1 и θ2. Поскольку cos θ = [1 + tg2α]−1
2 = [1 + (∂y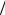
∂x )2]−1
2 , то с учетом не-
равенства (∂y
∂x )2 <<1, можно записать cos θ1 ≈ cos θ2 ≈1. Это позво-
ляет пренебречь деформацией длины участка AB в процессе колеба- ний.
В случае отсутствия внешних сил и демпфирования уравнение
движения струны (3.6) будет иметь вид ρ ∂2y = F ∂2y , или
∂t2 ∂x2
99
1 ∂2y |
= |
∂2y |
, |
c2 = |
F . |
(3.7) |
||
|
|
|
||||||
c2 ∂t2 |
∂x2 |
|||||||
|
|
|
ρ |
|
||||
Как видим, уравнение (3.7) совпадает с уравнением (3.1), которое бы- ло получено вследствие перехода от дискретной системы к непрерыв- ной. Уравнение (3.7) — это частный случай хорошо изученного в ма- тематической физике волнового уравнения. Уравнение такого вида и его обобщение на двумерные и трехмерные случаи в книге будут встречаться часто. Уравнение (3.7) можно интерпретировать так: ус-
корение струны ∂2y
∂t2 , обусловленное натяжением в каждой точке,
тем больше, чем больше кривизна струны ∂2y
∂x2 . При принятых ус- ловиях постоянная величина c в этом уравнении имеет размерность скорости, с, м
с . Ее значение определяется только внутренними
свойствами системы (F и ρ), а физическое содержание будет опреде- лено ниже.
3.3. Общее решение уравнения движения струны. Движение при заданных начальных условиях
3.3.1. Решение Д'Аламбера для бесконечной струны
Уравнение движения струны (3.7) было впервые получено в 1747 г. Д'аламбером . Он нашел его общее решение, которое рас- крывает главные черты поведения такой колебательной системы, как струна.
Для построения решения (3.7) введем новые пространственно- временные координаты
ξ = x +ct, η = x −ct. |
(3.8) |
Ясно, что такие соотношения устанавливают взаимно однозначное соответствие между парами чисел (x,t) и (ξ,η). Используя правила вы-
числения производных в новых координатах, получаем ∂∂yx = ∂∂ξy ∂∂ξx + ∂∂ηy ∂∂ηx , ∂∂yt = ∂∂ξy ∂ξ∂t + ∂∂ηy ∂η∂t . Тогда исходное волновое урав-
нение (3.7) приобретает особенно простой вид
∂2y |
= 0. |
(3.9) |
|
∂ξ∂η |
|||
|
|
Решение уравнения (3.9), очевидно, будет иметь вид
Д’Аламбер (D’Alembert) Жан Лерон (1717—1783) — французский математик
ифилософ.
100