2 семестр / Теория на 29.06.20

Виды дифференциальных уравнений

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида  .

Дифференциальные уравнения с разделяющимися переменными вида   или  .

Дифференциальные уравнения   называют уравнениями с разделенными переменными.

Линейные неоднородные дифференциальные уравнения первого порядка  .

Дифференциальное уравнение Бернулли  .

Уравнения в полных дифференциалах  .

Дифференциальные уравнения второго порядка.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами  .

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами  .

Линейные однородные дифференциальные уравнения (ЛОДУ)   и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка  .

Дифференциальные уравнения высших порядков.

Дифференциальные уравнения, допускающие понижение порядка.

Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами   и  .

Системы дифференциальных уравнений вида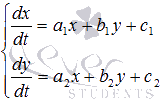 

Изображение и оригинал

Основными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.

Пусть  – действительная функция действительного переменного (под будем понимать время или координату).

Функция  называется оригиналом, если она удовлетворяет следующим условиям:

1.  при

2.  – кусочно-непрерывная при т. е. она непрерывна или имеет точки разрыва 1-го рода, причем на каждом конечном промежутке оси таких точек только конечное число, причем

3. Существуют такие числа  что для всех выполняется неравенство , т. е. при возрастании функция может возрастать не быстрее некоторой показательной функции. Число (точная нижняя граница такихs) называется показателем роста  .

Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент  Третьему условию удовлетворяют ограниченные функции степенные и многие другие.

Не являются оригиналами, например, функции вида  (не выполняется условие 3), функции  (не выполняется условие 2).

Условия 1) – 3) выполняются для большинства функций, описывающих различные физические процессы.

Замечание. Функция  может быть и комплексной функцией действительного переменного, т. е. иметь вид она считается оригиналом, если действительные функции и являются оригиналами.

Изображением оригинала  называется функция комплексного переменного , определяемая интегралом

(1)

Операцию перехода от оригинала  к изображению называют преобразованием Лапласа. Соответствие между оригиналом  и изображением записывается в виде или , а также (принято оригиналы обозначать малыми буквами, а их изображения – соответствующими большими буквами).

Ряды

Числовым рядом называется сумма вида

, (1.1)

где  , , ,…, ,…, называемые членами ряда, образуют бесконечную последовательность; член называется общим членом ряда.

Частичная сумма числового ряда – это сумма вида  , где n – некоторое натуральное число.   называют также n-ой частичной суммой числового ряда.

Числовой ряд   называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд   называется расходящимся.

Числовой ряд   называется знакоположительным, если все его члены положительны, то есть,  .

Числовой ряд   называется знакочередующимся, если знаки его соседних членов различны. Знакочередующийся числовой ряд можно записать в виде   или  , где  .

Числовой ряд   называется знакопеременным, если он содержит бесконечное множество как положительных, так и отрицательных членов.

Знакочередующийся числовой ряд является частным случаем знакопеременного ряда.

Ряды 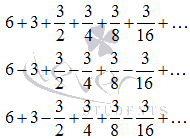являются знакоположительным, знакочередующимся и знакопеременным соответственно.

Свойства сходящихся числовых рядов.

1. Если сходится числовой ряд  , то сходящимся будет и ряд 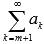 . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду   добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.

2. Если сходится числовой ряд   и его сумма равна S, то сходящимся будет и ряд 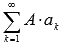 , причем 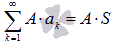 , где A – произвольная постоянная.

3. Если сходятся числовые ряды   и  , их суммы равны A и B соответственно, то сходящимися будут ряды 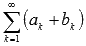  и  , причем их суммы будут равны A + B и A - B соответственно.

Необходимое условие сходимости ряда.

Если числовой ряд   сходится, то предел его k-ого члена равен нулю:  .

При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если  , то ряд расходится.

С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства   не говорит о сходимости числового ряда  . К примеру, для гармонического ряда   необходимое условие сходимости выполняется  , а ряд расходится.

Признак Даламбера.

Пусть   - знакоположительный числовой ряд. Если  , то числовой ряд сходится, если  , то ряд расходится.

Радикальный признак Коши.

Пусть   - знакоположительный числовой ряд. Если  , то числовой ряд сходится, если  , то ряд расходится.