
- •Вариант 20.
- •Составить таблицу истинности:
- •Доказать законы алгебры логики:
- •3. Упростить формулы, использую законы алгебры логики.
- •4. Составить таблицу истинности для формул.
- •5. Определить тип формулы: тавтология, выполнима или невыполнима.
- •6. Построить конъюнктивную нормальную форму и дизъюнктивную нормальную форму для таблично заданной функции.
- •7. Построить переключательную схему для конъюнктивной нормальной формы и дизъюнктивной нормальной формы функции из задания 6.
- •8. Описать метод сортировки «Внутренняя сортировка. Сортировка выбором».
- •9. Составить программу для машины Тьюринга.
- •10. Описать числа с плавающей точкой.
- •11. Определите и объясните, какие ip – адреса не могут быть назначены хостами.
6. Построить конъюнктивную нормальную форму и дизъюнктивную нормальную форму для таблично заданной функции.
Таблица 6.
x |
y |
z |
F |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
6.1) Конъюнктивная нормальная форма:
F(x, y, z) = (x + y + z) * (x + y + ¬ z) * (¬ x + ¬ y + ¬ z) =
= (x + y) * (¬ x + ¬ y + ¬ z).
6.2) Дизъюнктивная нормальная форма:
F(x, y, z) = ¬ x * y * ¬ z + ¬ x * y * z + x * ¬ y * ¬ x + x * ¬ y * z +
+ x * y * ¬ z = ¬ x * y * (¬ z + z) + x * ¬ y *(¬ z + z) + y * ¬ z (¬ x + x) =
= x * ¬ y + y * ¬ x + y * ¬ z.
7. Построить переключательную схему для конъюнктивной нормальной формы и дизъюнктивной нормальной формы функции из задания 6.
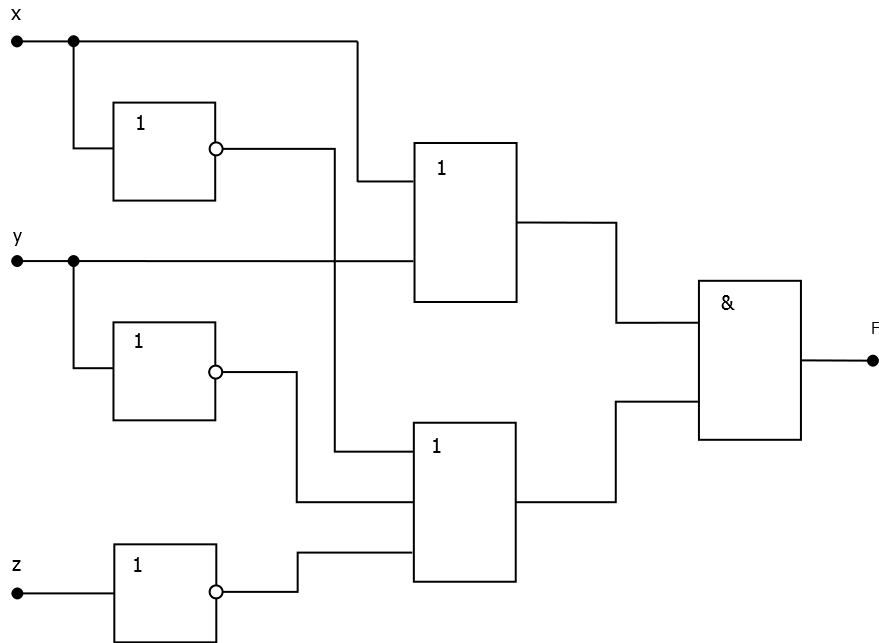
7.1) Конъюнктивная нормальная форма:
F(x, y, z) = (x + y) * (¬ x + ¬ y + ¬ z).
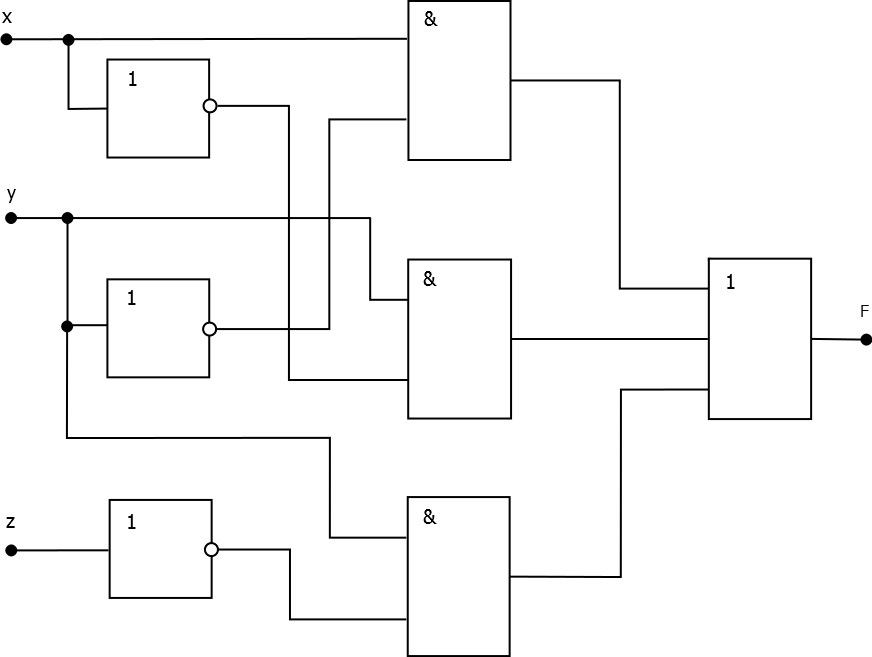
7.2) Дизъюнктивная нормальная форма:
F(x, y, z) = x * ¬ y + y * ¬ x + y * ¬ z.
8. Описать метод сортировки «Внутренняя сортировка. Сортировка выбором».
Сортировка выбором (Selection sort) – неустойчивый алгоритм сортировки, который можно описать следующим образом. Пусть задан массив, содержащий n элементов. Для сортировки его элементов по возрастанию, этот алгоритм будет иметь следующую последовательность шагов:
1. Шаг инициализации. Минимальным элементом принимается текущий i-ый элемент массива;
2. Шаг
итерации. Для
всех последующих элементов j ![]() находится
индекс минимального элемента массива.
Если найденный индекс не совпадает с
индексом текущего элемента, то текущий
и минимальный элементы меняются местами.
находится
индекс минимального элемента массива.
Если найденный индекс не совпадает с
индексом текущего элемента, то текущий
и минимальный элементы меняются местами.
3. Шаг
выхода. Предыдущие
шаги повторяются для всех элементов
массива с номерами ![]() .
Пример:
.
Пример:
Проход 1
20 |
10 |
40 |
30 |
50 |
i = 0 imin = 1
10 |
20 |
40 |
30 |
50 |
Проход 2
10 |
20 |
40 |
30 |
50 |
i = 1 imin = 1
10 |
20 |
40 |
30 |
50 |
Проход 3
10 |
20 |
40 |
30 |
50 |
i = 2 imin = 3
10 |
20 |
30 |
40 |
50 |
Проход 4
10 |
20 |
30 |
40 |
50 |
i = 3 imin = 3
10 |
20 |
30 |
40 |
50 |
Анализ
вычислительной сложности данного
алгоритма показывает, что для сортировки
необходимо осуществить (n-1)
проход на каждом i-ом
проходе, где ![]() ,
необходимо провести (n-i-1)
сравнений. Общее число сравнений
,
необходимо провести (n-i-1)
сравнений. Общее число сравнений ![]() .
Таким образом, по числу сравнений
алгоритм имеет порядок сложности
.
Таким образом, по числу сравнений
алгоритм имеет порядок сложности ![]() .
.
Число
перестановок элементов зависит от
первоначального расположения элементов
в массиве. В наилучшем случае, когда
массив упорядочен по возрастанию,
перестановок элементов не будет. В
наихудшем случае, когда массив упорядочен
по убыванию потребуется (n-1)-а
перестановка. В среднем число перестановок
будет ![]() .
.
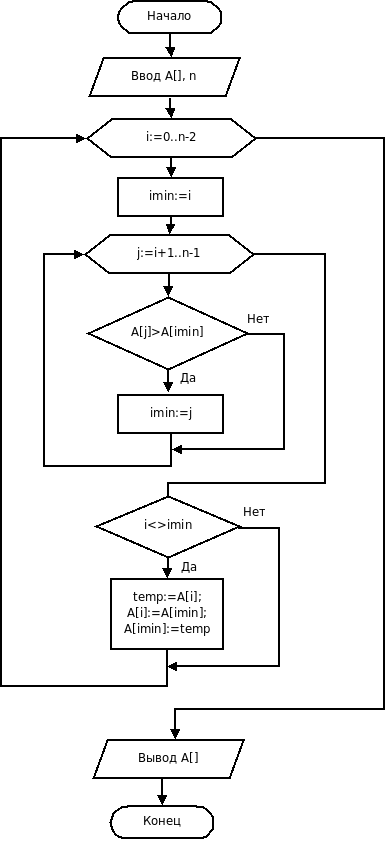
Блок-схема алгоритма сортировки выбором
