1_БСТ2154_Архангельский-3

Лабораторная работа №5

Тема 4.5. «Программирование алгоритмов регулярных циклических структур»

• ФИО — Архангельский Максим Вячеславович

• Группа — БСТ2154

• Номер студенческого билета — ЗБСТ21001

• Вариант №1

1. Тема и название работы:

Программирование алгоритмов регулярных циклических структур. Получение таблицы значений функции y=f(x) на отрезке [a;b] с шагом h.

2. Задание на разработку и вариант задания:

Создать приложение c именем Проект-4-5-Лаб для получения таблицы значений функции y = f(x) при изменении x на отрезке [a;b] с шагом h.

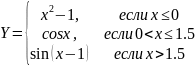
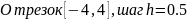
3. Формализация и уточнение задания

Данная задача решается с помощью процедуры-подпрограммы RegCikl(), которая, получив в качестве входных параметров (по значению) границы интервала(a и b) и шаг (h) изменения аргумента, табулирует функцию. В свою очередь, процедура RegCikl() вызывает функцию Fun(x), которая и вычисляет значение заданной функции от заданного аргумента.

4. Разработка проекта:

   1. Разработка графического интерфейса пользователя

Анализируя задание на разработку проекта, можно сделать вывод, что для организации ввода и вывода данных можно использовать пять элементов управления.

Элемент управления ListBox используется для вывода списка значений аргументов и списка значений функции.

Элемент управления Panel используется группировки элементов ListBox.

Текстовое поле элемента TextBox используется как для вывода исходных данных, так и для отображения результатов, получаемых в этой программе.

Элемент Label используется для размещения на форме поясняющих надписей.

Кнопка Button используется для запуска и окончания программы и инициализируется щелчком левой кнопки мыши.

Таким образом, форма может иметь вид, показанный на рисунке 1.

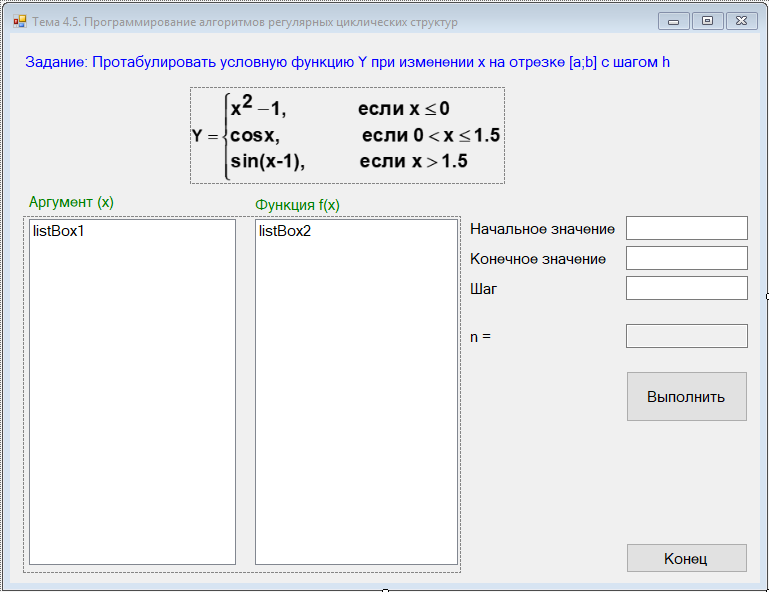
Рисунок 1 – форма приложения

2. Установка свойств объектов

В таблице 1 определены свойства объектов.

Таблица 1

Объект	Имя объекта	Свойство	Значение свойства
Форма	Form1	Name	Form1
		Text	Тема 4.5. Программирование алгоритмов регулярных циклических…
		Font	Microsoft Sans Serif; 11,25pt
Поле рисунка	pictureBox1	Name	pictureBox1
Метка	label1	Text	Задание: Протабулировать функцию Y при изменении x на отрезке [a;b] c шагом h
		ForeColor	Blue
Метка	label2	Text	Аргумент (x)
		ForeColor	Green
Метка	label3	Text	Функция f(x)
		ForeColor	Green
Метка	label4	Text	Начальное значение
Метка	label5	Text	Конечное значение
Метка	label6	Text	Шаг
Метка	label7	Text	n =
		ReadOnly	True
Текстовое поле	textBox1	Name	textBox1
Текстовое поле	textBox2	Name	textBox2

Продолжение таблицы 1

Объект	Имя объекта	Свойство	Значение свойства
Текстовое поле	textBox3	Name	textBox3
Текстовое поле	textBox4	Name	textBox4
Панель	panel1	Name	panel1
Список	listBox1	Name	listBox1
Список	listBox2	Name	listBox2
Кнопка	button1	Name	button1
		Text	Выполнить
Кнопка	button2	Name	button2
		Text	Конец

3. Разработка схемы алгоритма решаемой задачи

Блок-схема алгоритма функции Fun() представлена на рисунке 2, процедуры RegCikl() – на рисунке 3.

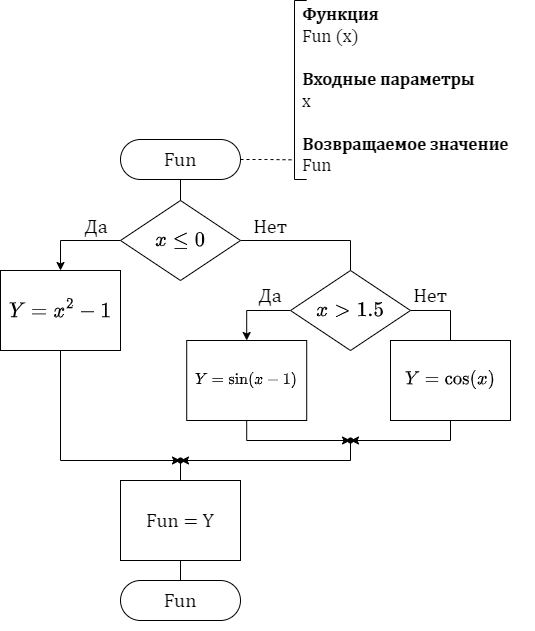
Рисунок 2 - схема алгоритма функции Fun()

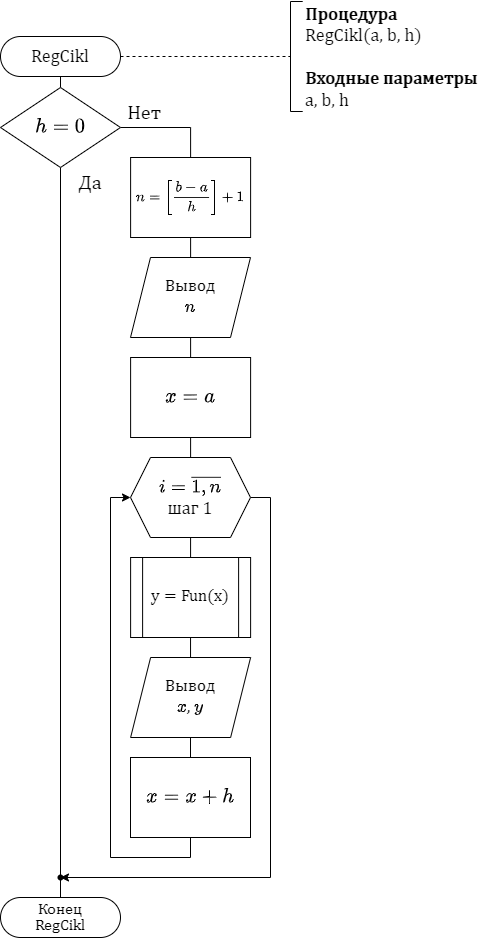
Рисунок 3 - схема алгоритма функции RegCikl()

4. Написание программного кода

Программный код представлен ниже.

//функция получения из TextBox действительного числа

double vvod(TextBox textbox)

{

return Convert.ToDouble(textbox.Text);

}

//процедура вывода в TextBox целого числа

void vivodint(TextBox textbox, int n)

{

textbox.Text = Convert.ToString(n);

}

//процедура форматированного вывода результата в listBox

void vivodlist(ListBox l, double z)

{

l.Items.Add(z.ToString("F16"));

}

double Fun(double x)

{

double Y;

if (x <= 0)

{

Y = Math.Pow(x, 2) - 1;

}

else if (x > 1.5)

{

Y = Math.Sin(x - 1);

}

else

{

Y = Math.Cos(x);

}

return Y;

}

void RegCikl(double a, double b, double h)

{

double x, y;

int i, n;

if (h == 0) return;

n = Convert.ToInt32(Math.Ceiling((b - a) / h) + 1);

vivodint(textBox4, n);

x = a;

for (i = 1; i <= n; i++) {

y = Fun(x);

vivodlist(listBox1, x);

vivodlist(listBox2, y);

x += h;

}

}

private void button1_Click(object sender, EventArgs e)

{

double a, b, h;

a = vvod(textBox1);

b = vvod(textBox2);

h = vvod(textBox3);

RegCikl(a, b, h);

}

5. Результаты выполнения проекта

Результат выполнения проекта приведен в таблице.

Аргумент X	Функция f(x)
-4	15
-3,5	11,25
-3	8
-2,5	5,25
-2	3
-1,5	1,25
-1	0
-0,5	-0,75
0	-1
0,5	0,8775825618903730
1	0,5403023058681400
1,5	0,0707372016677029
2	0,8414709848078970
2,5	0,9974949866040540
3	0,9092974268256820
3,5	0,5984721441039570
4	0,1411200080598670

6. Доказательство правильности результатов

Анализируя результаты, полученные после выполнении проекта, можно сделать вывод, что результаты верны.