Добавил:

kolrrro Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Физика

Файл:

Архангельский М.В. БСТ-2154 КР№2 Физика

.pdf

Скачиваний:

Добавлен:

04.04.2023

Размер:

833.31 Кб

Скачать

☆

Министерство цифрового развития связи и массовых коммуникаций Российской федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики»

Контрольная работа №2

Вариант 1

Выполнил: Архангельский Максим Вячеславович студент 2 курса группы БСТ-2154

студенческий билет №ЗБСТ21001

Москва 2022г.

m = 48 г = 0,048 кг

t1 = 2,5 с

η = 80% e = 2,718

r ― ? t2 ― ?

Задача 201

Тело массой 48 г совершает затухающие колебания на пружине, погруженной в вязкую жидкость. Найти коэффициент сопротивления среды r, если за 2,5 с колебательная система теряет 80% своей энергии. Определить, через какое время амплитуда смещения тела уменьшиться в e = 2,718 раз.

Решение:

Зависимость амплитуды затухающих колебаний от времени

A(t) = A0e− t ,

где А0 ― амплитуда колебаний в момент t = 0; β = r/(2m) ― коэффициент затухания;

m — масса колеблющегося тела,

r — коэффициент сопротивления среды. Энергия пропорциональна квадрату амплитуды:

A(t ) = A e		− t	,
A(t ) = A e		1	,
		1
1	0

W(t1 ) =W0e−2 t1 ,

= W (t1 ) = e−2 t1 ; W0

− 2 t		= ln ;
1
= −	ln		;
= −		2t	;
		2t
		1
r = 2m = −2m				ln	= −2 0,048	ln 0,8		= 0,00428 кг/с.
r = 2m = −2m				2t	= −2 0,048	2	2,5	= 0,00428 кг/с.
				2t		2	2,5
				1

За время t2 амплитуда уменьшится в e раз:

A(t			2		) = A e− t2				,
			2				0
e =					A0		= e t2 ,
e =				A(t2 )			= e t2 ,
				A(t2 )
t2					=1,
t		=			1	= −		2t1	= −	2 2,5	= 22,4 с.
t	2	=				= −			= −		= 22,4 с.
	2							ln		ln 0,8
								ln		ln 0,8

Ответ: r = 0,00428 кг/с; t2 = 22,4 c.

Задача 211

Амплитуды и периоды двух одинаково направленных гармонических колебаний равны, фазы же различаются на 2π/3. Уравнение результирующего колебания в единицах СИ имеет вид x = 0,2cos(πt+π). Определить уравнения слагаемых колебаний.

A1 = A2 = A

T1 = T2 = T

φ2 – φ1 = 2π/3

x = 0,2cos(πt+π)

x1(t) ― ? x2(t) ― ?

Решение:

Циклические частоты слагаемых колебаний

	=		= =	2	.
		2
1				T

Так как уравнение результирующего колебаний x = Acos( t + ) = 0,2cos( t + ) =

= 0,2sin( t + + / 2) = 0,2sin( t + 3 / 2), то ω = π рад/с, Aрез = 0,2 м.

Амплитуда результирующего колебания

А			=					А	2	+			А			2			+ 2А А cos(													− ) =
А			=					А		+			А						+ 2А А cos(											2		− ) =
рез								1						2							1			2						2				1
=				А	2	+ А				2		+ 2А								2	cos	2						= A		= 0,2 м.
					2					2										2
																							3
																							3
Начальная фаза результирующего колебания
tg =						А sin											+ А sin											=		А sin						+ А sin					=
tg =								1						1							2					2		=						1					2		=
								1						1							2					2								1					2
						А cos											+ А cos										2		А cos							+ А cos				2
								1						1							2						2							1						2
		sin						+ sin								2						3
=						1										2				= tg					.
=	cos							+ cos												= tg					.
	cos							+ cos									2
						1											2
Учитывая, что φ2 = 2π/3 + φ1, получим
tg =						sin + sin( 2																/ 3 + )									=
tg =											1																	1			=
											1																	1
						cos + cos(2																/ 3 + )
											1																	1
		sin + sin												2						cos				+ sin								cos		2			sin				+			3	cos	−	1	sin
		sin + sin																		cos				+ sin								cos					sin				+				cos	−		sin
						1								3								1							1					3			1					2				1	2	1
=														3																				3		=						2					2		=
=															2														2							=						1					3		=
	cos + cos														2					cos				− sin					2				sin				cos −					1		cos −			3	sin
	cos + cos																			cos				− sin									sin
						1										3						1							3					1								2					2
																3													3								1					2				1	2	1
																																					1									1		1

		1		sin +										3			cos								sin 1					+					cos 1
																																		3						3

=	2							1					2								1	=																= tg					= .


		1		cos			1 −							3				sin 1							cos 1 −									3 sin 1
	2			cos			1 −						2					sin 1
	2												2

Подберем угол: φ1 = π/6+πn, рад; n = 0, 1, 2, ...

1) Если φ1 = π/6, то

рад.

Уравнения слагаемых колебаний:

= A1sin ( t + 1 ) = 0,2sin t +

5π/6

π/6

= A2sin ( t + 2 ) = 0,2sin t +

3π/2

Результирующее колебание

x = 0,2sin

t +

3 .

Из рисунка видно, что сумма векторов

не равна вектору

2) Если φ1 = 7π/6, то

рад.

Уравнения слагаемых колебаний:

x1 = A1sin ( t + 1 ) =

0,2sin t

= A2sin ( t + 2 ) = 0,2sin t +

7π/6

t −

= 0,2sin

–π/6

3π/2

Результирующее колебание

x = 0,2sin

t +

Ответ: x1 = 0,2sin(πt + 7π/6), x2 = 0,2sin(πt – π/6).

Задача 221

Плоская электромагнитная волна, имеющая максимальную напряженность электрического поля 20 В/м и частоту 106 Гц, распространяется в вакууме. Определить уравнение электромагнитной волны с числовыми коэффициентами, выбрав начальные условия. Найти интенсивность волны. Привести снимок и осциллограмму подобной волны.

Em = 20 В/м

ν = 106 Гц

υ = c

E(t) ― ?

I ― ?

Решение:

Уравнение плоской волны

E(x, t) = E	m	cos (t − x / ),
	m

где E(x, t) — напряженность в точке с координатой x в момент t;

ω = 2πν — круговая частота; υ — скорость распространения колебаний в среде (фазовая скорость).

= 2 10

рад/с;

E(x, t) = 20 cos 2 10

−

= 20 cos(6,28 10

− 0,0209 x).

Интенсивность электромагнитной волны

	1				2
I =		0		E	2	,
I =	2			E	m	,
					m
			0
			0

где Em — амплитуда напряженности электрического поля.

I =	1	1 8,85 10 −12		20 2	= 0,531 Дж/(м 2 с).
	2		1 4 10 −7

Чтобы получить снимок, нужно зафиксировать время, например, t = 0. E(x,0) = 20cos(0,0209x).

20
10
E, В/E(мx)
0	100	200	300	400	500
10
20
			x, м
			x

Чтобы получить осциллограмму, нужно зафиксировать координату, например, x = 0.

E(0, t) = 20 cos(6,28 10	6	t ).
E(0, t) = 20 cos(6,28 10		t ).
20
10

E, ВE(/мx)

0.001

0.002

0.003

0.004

t, с

x Ответ: E(x, t) = 20cos(6,28∙106t – 0,0209x); I = 0,531 Дж/(м2∙с).

Задача 231

На сколько изменится расстояние между максимумами яркости смежных интерференционных полос на экране наблюдения интерференционной картины в опыте Юнга, составляющее 1,2 мм, если фиолетовый светофильтр (0,44 мкм) заменить красным (0,66 мкм)?

x1 = 1,2 мм λ1 = 0,44 мкм λ2 = 0,66 мкм

x2 ― ?

Решение:

Из рисунка:
tg =	x	;
tg =	l	;
	l
sin =			,
sin =	d		,
	d

где — разность хода лучей 1 и 2.

		x
		A
		A
1		x
	α
d		О

Так как для малых углов выполняется

tg sin ,
то
	x	=		;
	l		d

= xdl .

Условие максимумов интерференции:

= m , m = 0,1, 2, ...,

где m — номер максимума. Приравняем выражения для Δ:

xdl = m .

Найдем расстояние x между соседними максимумами:

=m l x ;

x + x =

(m +1) l

;

x = (x + x) − x =

(m +1) l

−

m l

Для длин волн λ1

и λ2

соответственно имеем

;

0,66 мкм

1,2 мм =1,8 мм.

0,44 мкм

Ответ: x2 = 1,8 мм.

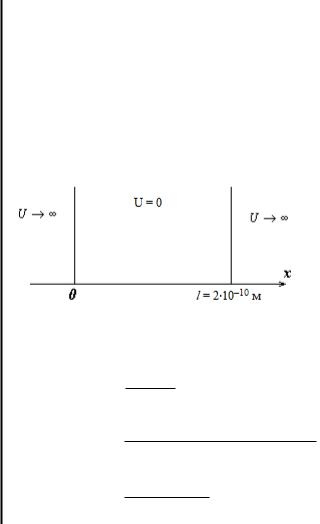
Задача 241

Электрон находится в потенциальном ящике шириной 0,2 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.

Решение:

l = 2∙10–10 м

Собственное значение энергии частицы на соседних

Еmin — ?

энергетических уровнях в потенциальном ящике:

;

(n +1)

2ml

n+1

2ml

Е = En+1 − En =

2 22

(n +1)2 − n2 =

2 22 2n +1 .

2ml

ΔE будет минимальным при n = 1.
			3		2			2
					2			2
Е	min	=	2ml				2			;
	min						2

					3				2		(1,05			10	−34	)		2
Е		=			3						(1,05			10		)					= 4,48 10	−18	Дж;
																						−18
	min		2	9,11 10									−31	(2 10			−10		)	2
	min												−31				−10			2

			4,48						10			−18
Е		=	4,48						10				эВ = 28 эВ.
Е	min	=	1,6			10					−19		эВ = 28 эВ.
	min										−19

Ответ: Еmin = 28 эВ.

Задача 251

Частица находится в потенциальном ящике. Найти соотношение разности соседних энергетических уравнений En, n+1 к энергии En частицы в случаях:

1) n = 2, 2) n = 10.

						Решение:
1) n = 2	Полная энергия частицы, движущейся в потенциальной
2) n = 10	яме с бесконечно высокими непроницаемыми стенками
En, n+1/En ― ?				h	2	n	2
En, n+1/En ― ?	E		=	h		n		,
	E	n	=				2	,
		n					2
				8m L
						0

где h — постоянная Планка; n — номер уровня энергии; m0 — масса покоя частицы;

L — ширина одномерной потенциальной ямы.

Тогда соотношение разности соседних энергетических уравнений En, n+1 к энергии En частицы

− E

(n +1)

n, n+1

n+1

8m L

−1 =

−1

−1 =

8m L

+ 2n +1

2n +1

−1

1) n = 2
	En, n+1		=	2 2 +1		=1,25.
	E		=	2	2	=1,25.
					2
		n
		n
2) n = 10
	En, n+1		=	2 10 +1			= 0,21.
	En		=	10 2			= 0,21.
	En			10 2

Ответ: 1) 1,25; 2) 0,21.

Соседние файлы в предмете Физика

#
04.04.202372.7 Кб34211.doc
#
04.04.202350.69 Кб31221.doc
#
04.04.202348.13 Кб24231.doc
#
04.04.2023325.12 Кб29241.doc
#
04.04.202361.95 Кб19251.doc
#
04.04.2023833.31 Кб15Архангельский М.В. БСТ-2154 КР№2 Физика.pdf
#
04.04.2023315.94 Кб36Архангельский М.В. БСТ-2154 л.р. Механические колебания вариант 1.pdf
#
04.04.202321.96 Кб172Лабораторная работа №1.docx
#
04.04.2023262.01 Кб93Лабораторная работа №20.docx
#
04.04.202312.06 Mб14Физика ч.2. ЗОТФ (БСТ 2к.) 2021г.doc
#
04.04.2023240.46 Кб23Экзамен Архангельский М.В. БСТ2154.pdf