4.3. Алгоритм применения стационарной теории возмущений для дискретного невырожденного спектра.
4.3.Алгоритм применения теории возмущений.
1.Записать гамильтониан в виде
|
|
|
|
|
|
|
|
|
|
H H0 |
V H0 |
W . |
|
|
|||
2. |
Решить уравнение Шрёдингера для «невозмущенной» задачи |
|
||||||
|
|
|
|
(0) |
(0). |
|
|
|
|
H |
0 |
|
|
||||
|
|
|
n |
n |
n |
n и |
n(0) . |
|
3. |
Найти по возможности все (или как можно больше) |
|||||||
Дальнейшие действия следует выполнить для всех энергетических уровней «возмущённой» системы
4. Определить первую поправку к энергии уровня номер l в теории
возмущений : |
|
|
|
|
|
ˆ |
|
|
|
||||||||
E |
(1) |
W |
|
|
|
|
x dx. |
|
|
|
x W |
|
|||||
Интеграл следует вычислить по всей области определения волновых функций «невозмущённой» системы. В случае, если интеграл определяется численно, а пределы интегрирования бесконечные, следует проверить результаты на сходимость при x → ± ∞.
E 0 |
E(1). |
|
|
|
|
4.3.Алгоритм применения теории возмущений.
5.Определить первую поправку к волновой функции
(1) |
(1) |
|
(1) |
|
|
W |
|
|
|
W |
|
|
|
||
|
am m (x), |
где |
am |
|
|
|
m |
|
|
|
|
m |
. |
||
E |
(0) |
|
|
|
|
|
|||||||||
|
m |
|
|
|
|
m |
|
|
|
|
m |
||||
|
|
|
|
|
|
|
|
|
|
||||||
Суммирование производится по всем собственным значениям дискретного спектра энергий. Число возможных волновых функций – такое же, сколько известно собственных значений энергии «невозмущенной» задачи.
Волновая функция с учетом поправок первого порядка теории возмущений:
|
x x |
Wm |
m x . |
(1) |
|
|
m m
6. Определить вторую поправку к энергии уровня номер l:
E(2) 2 |
|W m |2 |
, |
где |
W m (x)W (x) m (x)dx. |
|
||||
m m |
|
|
|
|
Энергия уровня номер l с учетом второй поправки теории возмущений:
E W 2 |W m |2 . m m
7. Далее можно продолжить ряд теории возмущений, вычислив вторую поправку к волновой функции, третью поправку к энергии и так далее.
4.4. Пример применения стационарной теория возмущений для дискретного невырожденного спектра.
Непрямоугольная яма с бесконечными стенками
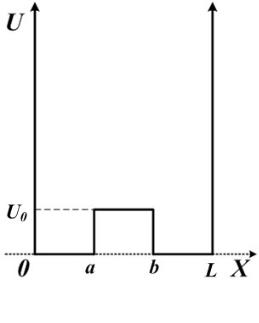
4.4. Непрямоугольная яма с бесконечными стенками.
Мы в качестве примера системы, допускающей решение методом теории возмущений, рассмотрим бесконечную потенциальную яму (яму со стремящимися к бесконечности стенками), на дне которой потенциальная энергия U ≠ 0.
, |
x 0 |
|
0 x a |
0, |
|
|
, a x b |
U U1 |
|
0, |
b x L |
|
x L |
, |
|
|
|
В качестве «невозмущённой» задачи будем рассматривать задачу о яме с бесконечными стенками шириной L, решение которой было подробно рассмотрено ранее. Известно, что собственные значения энергии в этом частицы массой m в такой потенциальной яме равны
En n 2 2 n2. 2mL2
Волновые функции частицы в такой потенциальной яме
n x |
2 |
n |
|
|
2 |
sin nkx , |
|
. |
||
L |
sin |
L |
x |
L |
k |
L |
||||
|
|
|
|
|
|
|
||||
Согласно теории возмущений собственные значения энергии будем определять по формуле
|
E W 2 |
|W m |2 |
. |
||||
|
|
||||||
|
|
|
|
m m |
|||
Волновые функции частицы |
|
|
Wm |
m x . |
|||
|
x x |
||||||
(1) |
|
|
|
|
|
||
|
|
|
m m |
|
|
||
Здесь |
|
|
ˆ |
|
|
|
|
|
|
(x)W (x) m (x)dx. |
|||||
|
W m |
||||||
В рассматриваемом случае волновые функции частицы действительны, поэтому
W m (x)U (x) m (x)dx.
Формально, интеграл должен быть вычислен по всей области определения волновых функций, то есть
W m (x)U (x) m (x)dx.
В то же время известно, что при x < 0 и при x > L все волновые функции равны нулю, поэтому и интегралы по соответствующим областям также равны нулю.
|
L |
|
b |
|
|
W |
|
(x)U (x) |
(x)dx |
(x)U (x) |
(x)dx. |
m |
|
m |
|
m |
|
|
0 |
|
a |
|
|
Получим общую формулу для таких интегралов, потому что они встречаются и при вычислении поправок к энергии и при вычислении поправок к волновым функциям.
W |
b |
|
(x)U |
(x)dx b |
2sin |
kx |
U |
0 |
2 sin |
mkx |
dx |
||
m |
|
0 m |
|
L |
|
|
|
L |
|
|
|
||
|
a |
|
|
a |
|
|
|
|
|
|
|
||
2U0 b sin kx sin mkx dx.
L a
Выражения для интегралов (матричных элементов возмущения) получим для
двух случаев: |
|
|
|
1) |
m , |
2) |
m . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
W 2UL |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
W 2U0 |
0 a sin2 kx dx. |
|
|
2 kx |
|
dx |
|||||||||||||||
|
|
|
b sin2 kx dx 2U0 1 b |
|
1 cos |
|
||||||||||||||||||
|
|
|
|
|
|
L |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
L 2 a |
|
|
|
|
|
|
|
||||||
U |
b |
U |
b |
|
|
|
U |
|
|
|
U |
|
sin |
2 kb sin 2 ka . |
||||||||||
|
0 |
a dx |
|
0 |
a cos 2 kx dx |
|
L0 |
b |
a |
|
0 |
|||||||||||||
L |
|
L |
|
|
2 kL |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
L, |
|
|
|
|
|
2 kL 2 L L 2 . |
|
|
|
||||||||
|
|
|
|
|
U |
b |
a |
U |
0 |
|
|
|
b |
|
|
|
|
a |
||||||
|
|
|
|
W |
0 |
|
|
|
sin |
2 |
|
|
|
sin |
2 |
|
. |
|||||||
|
|
|
|
L |
|
|
|
L |
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
L |
|||||||||
2) m .
W m 2U0 b sin kx sin mkx dx. L a
|
|
sin sin 1 |
cos cos |
. |
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2U0 |
b |
|
|
|
|
2U0 |
1 b |
|
|
|
|
|
|
|
|
|
|
|||
W m L |
a sin kx sin mkx dx |
|
|
|
|
|
|
m |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
L |
2 a cos |
kx cos m kx dx |
||||||||||||||||||
|
UL0 |
b |
|
|
|
|
|
|
|
U0 |
|
b |
|
|
|
|
|
|||
|
a cos m kx dx |
|
a cos m kx dx |
|||||||||||||||||
|
L |
|||||||||||||||||||
|
|
|
U0 |
|
sin |
|
m |
|
kb |
|
sin |
|
|
ka |
|
|
||||
|
|
m kL |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|||||||||
|
U |
sin m kb |
|
m0 kL |
sin m ka .
m |
|
|
m kL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
W |
|
|
|
U0 |
|
|
|
|
|
|
sin |
|
|
m |
kb |
|
sin |
|
m |
ka |
|
|
|
||||||||
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
sin m |
kb sin m ka , |
|
||||||||||||||||||||
|
|
|
0 |
|
|
|
k L. |
||||||||||||||||||||||||
|
m kL |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
U0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W m |
|
|
|
|
|
sin |
m |
L |
b |
sin |
m |
L |
a |
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
U0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
sin |
m |
|
b |
|
|
sin m |
|
a |
. |
|
|
|||||||||||||
|
|
L |
L |
|
|
||||||||||||||||||||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Теперь осталось подставить полученные формулы для матричных элементов возмущения в формулы для энергии и волновой функции и выполнить вычисления.