c_Панков Практикум по АСП 22

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждениевысшего образования

Московский технический университет связи и информатики

К.Н. Панков

ПРАКТИКУМ ПО ДИСЦИПЛИНЕ «АНАЛИЗ СЛУЧАЙНЫХ ПРОЦЕССОВ»

Версия от 07.02.2022

Учебное пособие

для обучающихся в бакалавриате по направлении. 11.03.02 - Инфокоммуникационные технологии и системы связи

Москва 2022

Панков К.Н. Практикум по дисциплине «Анализ случайных процессов». Учебное пособие / МТУСИ. – М., 2022. - 91 с.

Данное учебное пособие предназначено для использования на практических занятиях по курсу «Анализ случайных процессов». Его цель – помочь студентам, овладевшим основами теории вероятностей, познакомиться с основными понятиями теории случайных процессов и овладеть методами решения задач, связанных с дискретными цепями Маркова, корреляционной теорией случайных процессов, случайными потоками и основами теории массового обслуживания.

Учебное пособие ориентировано на обучающихся в бакалавриате по направлению подготовки 11.03.02 - Инфокоммуникационные технологии и системы связи.

Ил. __, табл. __, список лит.__ назв.

Издание утверждено Методическим советом университета в качестве учебного пособия. Протокол No __от __.__.____г.

Рецензенты:

© Московский технический университет связи и информатики, 2022

2

Раздел № 1 Основные понятия. Стационарные процессы

1.1Пусть случайная величина равномерно распределена на отрезке [-1;1]. Чему равна вероятность события «Траектория процесса t образует с положительной полуосью абсцисс Оt острый угол больше 60 »?

1.2Пусть случайная величина равномерно распределена на отрезке [-2;2]. Чему равна вероятность события «Траектория процесса t образует с положительной полуосью абсцисс Оt острый угол по модулю меньше 60 »?

1.3Пусть случайная величина равномерно распределена на отрезке [-1;1]. Чему равна вероятность события «Траектория процесса t образует с положительной полуосью абсцисс Оt острый угол по модулю меньше 30 »?

1.4Пусть случайная величина равномерно распределена на отрезке [-2;2]. Чему равна вероятность события «Траектория процесса t образует с положительной полуосью абсцисс Оt острый угол по модулю больше 30 »?

1.5Пусть случайная величина имеет стандартное нормальное

распределение. Чему равно математическое ожидание случайного процесса a t b, где a,b - действительные числа?

1.6Пусть случайные величины и независимы и имеют функции распределения F (x) и F (y) соответственно. Найти конечномерные распределения (до порядка 3 включительно) случайного процесса (t)= t+ .

1.7Пусть случайные величины и независимы и имеют распределения: – равномерное на [-1; 0] и – равномерное на [0; 1]. Описать траектории случайного процесса (t)= t+ .

1.8Пусть случайные величины и независимы и имеют плотности распределения р (x) и р (y) соответственно. Для процесса (t)= t+ (1–t) найти

плотность p( (t1), (t2))(z1,z2).

1.9Пусть и независимы и имеют распределения: – равномерное на отрезке [-1,0] и – равномерное на отрезке [0,1]. Описать траектории случайного процесса (t)= t+ .

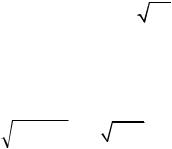
1.10Рассматривается случайная функция X(t) Ut2 2, где U – случайная величина, распределенная по нормальному закону N(2; 4). Найти функцию распределения сечения этой функции Ft x , математическое ожидание mX (t),

дисперсиюDX (t), X (t) и корреляционную функцию K X (t1,t2).

Решение. Согласно определению функции распределения случайной величины

3

Далее рассмотрим случай, когда t 0. Так как U N(2; 4),то

По определению

mX (t) E X t E Ut2 2 t2 EU 2,

DX (t) DX t D Ut2 2 t4 DU ,

X (t) 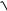DX t t2 DU ,

K X t1,t2 E X t1 mX t1 X t2 mX t2

E Ut12 2 t12 EU 2 Ut22 2 t22 EU 2 t12t22 DU .

Параметры нормального распределения являются его основными числовыми характеристиками (EU 2,DU 4). Следовательно,

mX (t) 2t2 2,DX (t) 4t4 , X (t) 2t2 ,K X t1,t2 4t12t22 .

константа. Найти математическое ожидание mX (t), дисперсию DX (t) и корреляционную функцию K X (t1,t2).

1.12 Рассматривается случайная функция X(t) U exp( t), где U случ. велич., распределенная по экспоненциальному закону Ex( ). Найти плотность распределения сечения, математическое ожидание mX (t), дисперсию DX (t), X (t) и корреляционную функцию K X (t1,t2).

1.13 Рассматривается случайная функция X(t) 2Ut2 2t , где U – случайная величина, распределенная по равномерному закону R( 1;3). Найти плотность распределения сечения, математическое ожидание mX (t), дисперсию DX (t), X (t) и корреляционную функцию K X (t1,t2).

1.14 Рассматривается случайная функция X(t) Ut3 t 1, где U – случайная величина, распределенная по закону R(0, 4). Найти закон распределения

4

DX (t), X (t) и корреляционную функцию K X (t1,t2).

9.1.

1.16 Рассматривается случайная функция X(t) Ut b, где U — случайная величина, распределенная по нормальному закону N(a; 2 ), b — неслучайная величина. Найти плотность распределения сечения этой случайной функции, математическое ожидание mX (t), дисперсию DX (t), X (t) и корреляционную

функцию K X (t1,t2).

1.17 Найти математическое ожидание mX(t), корреляционную функцию КX (t1,t2), дисперсию DX (t) случайного процесса Х(t). U, V некоррелированные случайные величины для случаев

a.Х(t) = t2 U + V cost sint. U ~ N(3; 2), V ~ Exp(0.5).

b.Х(t) = t U – 3е 3t V + cost. U ~ R[0; 6], V ~ Bi(10; 0.5).

c.Х(t) = et U – V cht + 3. U ~ Π(0.2), V ~ R[–2; 2].

d.Х(t) = U sint V t + t5. U ~ N(1; 2), V ~ Π(2).

e.Х(t) = t3 U– V cos t – 2. U ~ R[–1; 3], V ~ Exp(0.4).

f.Х(t) = 3 U sht – е3tV + cost. U ~ Exp(0.25), V ~ R[2; 4].

g.Х(t) = 3 + U sin2t – 4t V. U ~ Bi(10; 0.3), V ~ Π(3).

h.Х(t) = U cos3t – V sint – t. U ~ R[–3; 1], V ~ N(–1; 0.5).

i.Х(t) = t2 U – V cht + t2. U ~ Exp(0.1), V ~ Bi(20; 0.2).

j.Х(t) = еt U V sint + t. U ~ N(–2; 2), V ~ Exp(4).

k.Х(t) = е 3t U – V t + 2t. U ~ R[–3; 3], V ~ Bi(10; 0.6).

l.Х(t) = 3Usint – V еt – еt. U ~ Π(4), V ~ R[1; 3].

m.Х(t) = t2 – е 2t U – V t. U ~ N(–1; 0.7), V ~ Exp(0.5).

n.Х(t) = t U – V sin2t + 4t2. U ~ R[3; 6], V ~ N(2; 3).

o.X(t) = U cos3t – V t2 + 3. U ~ Π(5), V ~ R[–3; 5].

p.Х(t) = 5t + 3t2U – V е2t. U ~ N(–2; 1.5), V ~ Exp(0.2).

q.Х(t) = 5 + U sint – V t2. U ~ Bi(10; 0.1), V ~ N(3; 0.3).

r.Х(t) = t2 U – V cht + t. U ~ Π(2), V ~ R[–2; 4].

s.Х(t) = t + U sh2t – 2t V. U ~ N(–1; 2), V ~ Exp(1/3).

t.Х(t) = t U – V sint + cost. U ~ R[–2; 2], V ~ Bi(20; 0.4).

u.Х(t) = е–t + U cost – V t. U ~ Exp(1/4), V ~ R[–5; –1].

v.Х(t) = –t U cht + V cost. U ~ N(5; 2), V ~ Π(3).

w.Х(t) = t2 U – V t – е3t. U ~ R[3; 6], V ~ Bi(20; 0.5).

x.Х(t) = 3sint + 2U sht – V еt. U ~ Exp(2), V ~ R[–1; 5].

y.Х(t) = U cos2t V t – 4t. U ~ Π(2), V ~ N(3; 0.3)

1.18 Найти математическое ожидание, корреляционную функцию и дисперсию случайного процесса X(t), зависящего от Y и Z где Y и Z –

5

случайные величины, характеризуемые следующими числовыми характеристиками:

a.X(t) = Ysin2 t + Zcos t, EY=2, EZ = 1, DY = 0.1, DZ = 0.004, корреляция между случайными величинами Y и Z равна 0;

b.Ycos t + Zsin t + 5t, EY=1, EZ = 0.2, DY = 0.1, DZ = 0.05, корреляция между случайными величинами Y и Z равна 0;

c.Yt – Zt2, EY=3, EZ = 0.5, DY = 0.1, DZ = 0.05, корреляция между случайными величинами Y и Z равна 0;

d.t–3cost+Y(t + cost)+Zcos2t, EY=0, EZ = 0, DY = 1, DZ = 2, корреляция между случайными величинами Y и Z равна 0;

e.Ye-t + Zet, EY=2, EZ = -2, DY = 1, DZ = 1, корреляция между случайными величинами Y и Z равна 0;

f.Ye-t + Zsin t, EY=1, EZ = 2, DY = 1, DZ = 1, корреляция между случайными величинами Y и Z равна 0.

Решение. a. В рассматриваемом случайном процессе множители sin2 t и cos t не являются случайными величинами. Поэтому при определении математического ожидания процесса Х(t) они выносятся за знак математического ожидания случайных величин Y и Z. Математическое же ожидание суммы равно сумме математических ожиданий составляющих случайного процесса:

E[X(t)] = x(t) = sin2 t E[Y]+ cos t E[Z].

Подставляя в последнее выражение числовые значения E[Y] и E[Z], получим mX (t) 2sin2 t + cos t.

Поскольку случайные величины Y и Z некоррелированы, корреляционная функция процесса X(t) равна сумме корреляционных функций его составляющих. При этом коэффициенты (неслучайные процессы) выносятся за знак корреляционных функций случайных величин Y и Z в виде произведения неслучайных процессов в двух сечениях по времени t1 и t2. Учитывая также, что КY(t1, t2)=DY и KZ(t1, t2)=DZ, будем иметь

KX(t1, t2)=sin2 t1 sin2 t2 DY + cos t1 cos t2 DZ.

Подставляя числовые значения для DY и DZ, получим

KXX(t1, t2)=0.1 sin2 t1 sin2 t2 + 0.05 cos t1 cos t2.

Дисперсия случайного процесса X(t) определится как DX(t)=KX(t1, t2) при t1=t2=t:

DX(t) = 0.1 sin22 t + 0.05 cos2 t.

1.19 Найти математическое ожидание и корреляционную функцию суммы двух некоррелированных случайных функций X(t) и Y(t) с характеристиками

1.20 Пусть kX (τ) корреляционная функция стационарного случайного процесса X(t). Найти его спектральную плотность в следующих случаях:

k. SX (ω)= 4/(π(1+ω2)2).

10при 2,

l.SX (ω)=

0 при 2.

m.SX (ω)= 10(sin2ω)/ω2.

o. SX (ω)= 2exp( |ω|/9).

q. SX (ω)= 10/(π(4+ω2)).

t.SX (ω)= 32/(π (4+ω2)2).

u.SX (ω)= 6(1 cos2ω)/( πω2).

v.SX (ω)= 10(sin2ω)/ω.

w.SX (ω)= exp( ω2/4).

x.SX (ω)= 2exp( |ω|/4).

20при 5, y. SX (ω)=

0 при 5.

8

(т.е. с нулевыми математическими ожиданиями, единичными дисперсиями и нулевой ковариацией между ними) случайные величины. Найти автоковариационные функции этих процессов, а также взаимную ковариационную функцию этих процессов.

9

1.29 Дана случайная функция X(t) U exp( 4t), где U – случайная величина, распределенная по равномерному закону R(1;3). Найти характеристики

функции Y(t) exp(t) X(t) dX(t): mY (t), KY (t,t ). dt

1.30 Дана спектральная плотность стационарного случайного процесса X(t):

функции Z(t) X( )d 4X(t): mZ (t), KZ (t,t ).

0

1.33 Дана автоковариационная функция стационарного случайного процесса:

стационарным.

1.35 Стационарный случайный процесс X(t) имеет спектральную плотность

случайного процесса Y(t) a X(t) b и определить, будет ли он стационарным.

случайного процесса Z(t) 3X(t) dX(t) . dt

10