3. Расчет вероятностей ошибок

Все рассмотренные критерии, кроме минимаксного критерия, приводят к единому правилу решения - отношение правдоподобия сравнивается с порогом, зависящим от критерия. Обозначим этот порог, независимо от применяемого критерия, через С. Тогда имеем правило

. (3.1)

При необходимости будем заменять величину С соответствующим порогом согласно выбранному критерию. В рассмотренном случае говорят, что отношение правдоподобия инвариантно относительно выбранного критерия. Определим в явном виде функции правдоподобия и .

Функция правдоподобия - это плотность распределения вероятности выборочных значений при состоянии источника , т.е. при отсутствии сигнала. В этом случае реализации , где - реализации шума. Наиболее часто на практике используется модель нормального (гауссовского) шума n(t), имеющего плотность распределения вероятности

(3.2)

где a _i- математическое ожидание шума в момент ,

- дисперсия (мощность) шума в момент ,

D_R-определитель, элементами которой являются коэффициенты корреляции

корреляционной матрицы

,

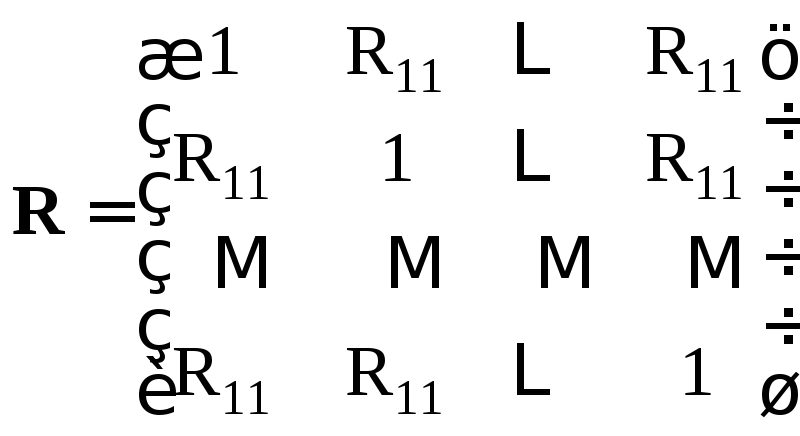- алгебраическое дополнение к элементу корреляционной матрицы.

Для нормального стационарного случайного процесса с некоррелированными значениями, (а значит с независимыми значениями) в моменты и математическим ожиданием, равным нулю, формула (3.2) упрощается:

, (3.3)

где - дисперсия (мощность) шума.

Учитывая соотношение , получим

. (3.4)

Функция правдоподобия - это плотность распределения вероятности выборочных значений при состоянии источника , т.е. при наличии сигнала в шуме. Учитывая, что сигнал и шум аддитивны, получим функцию правдоподобия

(3.5)

Используя выражения (3.4) и (3.5) запишем логарифм отношения правдоподобия и правило принятия решения (3.1)

.

Используя соотношение (3.1) и логарифм отношения правдоподобия получим правило обработки наблюдаемых данных

. (3.6)

Обозначим

, .

Правило принятия решения (3.1) запишется в виде

. (3.7)

Статистика представляет собой сумму независимых случайных значений , умноженных на неслучайные величины . Распределение вероятности - нормальное, параметры которого зависят от состояния источника. Известно, что сумма нормально распределенных величин распределена нормально. Следовательно, плотность вероятности величины равна

, (3.8)

где и - условные математическое ожидание и дисперсия случайной величины , зависящие от состояния источника .

Определим условные дисперсии и математические ожидания статистики Z, учитывая (1.1) и (1.2):

(3.9)

. (3.10)

Выразим вероятность ошибки a(2.1)и вероятность правильного принятия решения D = 1-b(2.4) через распределение статистики Z:

, (3.11)

. (3.12)

Интегральное представление вероятностей ошибок имеет вид

, (3.13)

, (3.14)

ãäå

. (3.15)

На рисунке 3.1 отображено поведение условных плотностей распределения w(z/s_j) при различных состояниях источника, а также вероятности ошибок первого и второго рода. Как видно, вероятности ошибок первого и второго рода равны площадям под кривой плотности распределения вероятности w(z/s_j) , j=0; 1.

Как видно из выражений (3.13) ¸(3.15), вероятность ошибкиaи вероятность правильного принятия решения D = 1 -bявляются функциями параметра d и порога С, который в свою очередь зависит от выбранного критерия. Если зафиксировать d, а порог С рассматривать как параметр, принимающий значения -¥< C <¥, то можно получить зависимость D(a), которая называется рабочей характеристикой. Ее можно построить, используя (3.13), (3.14). На рисунке 3.2 показан график D(a) для d₂ > d₁. В теории статистических решений доказывается, что

(3.16)

т.е. тангенс угла наклона касательной к кривой рабочей характеристики в некоторой точке (a, D) равен порогу обнаружения С. Таким образом, для заданных двух величин из четырех параметровa, D, С, и d с помощью рабочей характеристики можно найти два других параметра.