Калашников - Техническая Электродинамика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Санкт-Петербургский государственный университет аэрокосмического приборостроения

В. С. Калашников, А. В. Прусов

ТЕХНИЧЕСКАЯ

ЭЛЕКТРОДИНАМИКА

Направляющие системы и направляемые волны

Учебное пособие

Санкт-Петербург 2001

УДК 537.8 ББК 22.31

К17

Калашников В. С., Прусов А. В.

К17 Техническая электродинамика. Направляющие системы и направляемые волны: Учеб. пособие / СПбГУАП. СПб., 2001. 48 с.: ил.

Рассмотрены общие свойства направляемых волн и структура элект-

ромагнитного поля собственных волн в прямоугольном и круглом волноводах.

Пособие предназначено для студентов дневной и вечерней форм обучения по направлениям 200800 "Проектирование и технология РЭС" и 200700 "Радиотехника".

Рецензенты:

кафедра радиотехники Северо-Западного государственного заочного технического университета;

доктор технических наук профессор В. М. Балашов

Утверждено редакционно-издательским советом университета

в качестве учебного пособия

© Санкт-Петербургский государственный университет аэрокосмическогоприборостроения,2001

© В. С. Калашников, А. В. Прусов, 2001

2

1. ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1.1. Классификация линий передачи

Различают свободные и направляемые электромагнитные волны. Свободными называются электромагнитные волны, распространяющиеся в неограниченном пространстве. Направляемыми называются электромагнитные волны, распространяющиеся вдоль линий передачи.

Линией передачи называют устройство, ограничивающее область распространения электромагнитных волн и обеспечивающее движение потока энергии электромагнитной волны в заданном направлении. Линии передачи могут быть регулярными и нерегулярными, однородными и неоднородными.

Регулярной называют линию передачи, у которой поперечное сечение и электрофизические свойства заполняющих ее сред являются неизменными вдоль всей линии. Нерегулярной называют линию передачи, у которой нарушено хотя бы одно условие регулярности.

Однородной называют линию передачи, заполненную однородной средой. Неоднородной – линию передачи, заполненную неоднородной средой.

В зависимости от наличия или отсутствия в конструкции линии передачи замкнутого проводящего экрана, отделяющего область пространства, в которой распространяется направляемая волна, от окружающей среды, различают волноводы и открытые линии передачи. Волноводами называются линии передачи, в поперечном сечении которых имеется один или несколько замкнутых проводящих контуров, охватывающих область распространения направляемых волн.

Впоперечном сечении открытых линий передачи таких контуров нет. Геометрической характеристикой поперечного сечения линии пе-

редачи, определяющей количество изолированных проводящих поверхностей, входящих в состав ее конструкции, является «порядок связности» линии передачи. Различают односвязные, двухсвязные, многосвязные линии и линии передачи нулевой связности.

1.2. Некоторые виды линий передачи

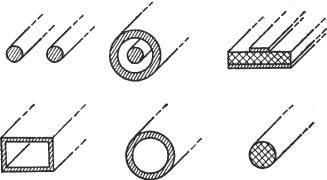
На рис. 1 приведены эскизы поперечных сечений некоторых видов линий передачи:

3

Рис. 1. Некоторые виды линий передачи

а – двухпроводная линия передачи (двухсвязная открытая линия передачи);

б – коаксиальный волновод (двухсвязный волновод с соосными внешним и внутренним проводниками);

в – микрополосковая линия передачи (двухсвязная открытая неоднородная линия передачи);

г – прямоугольный волновод (односвязный волновод, имеющий прямоугольное поперечное сечение);

д – круглый волновод (односвязный волновод, имеющий круглое поперечное сечение);

е – диэлектрическая линия передачи (открытая линия передачи нулевой связности).

1.3. Классификация электромагнитных волн, распространяющихся в линиях передачи

В зависимости от вида линий передачи в них могут распространяться электромагнитные волны четырех классов:

поперечные или Т-волны (старое название и обозначение – попереч- но-электромагнитные или ТЕМ-волны);

электрические или Е-волны (старое название и обозначение – попе- речно-магнитные или ТМ-волны);

магнитные или Н-волны (старое название и обозначение – попереч- но-электрические или ТЕ-волны);

гибридные волны.

4

Разделение волн, распространяющихся вдоль линий передачи, на указанные классы производится относительно продольной (направленной вдоль линии передачи) пространственной координаты z. По отношения к этой координате в Т-волнах векторы E и H имеют только поперечные (перпендикулярные оси 0z) составляющие; в Е-волнах вектор E имеет поперечную и продольную составляющие, а вектор H – только поперечную; в Н-волнах вектор H имеет поперечную и продольную составляющие, а вектор E – только поперечную; в гибридных волнах оба вектора ( E и H ) имеют и продольные и поперечные составляющие. Заметим, что в линиях передачи ось 0z совпадает с направлением движения распространяющихся вдоль этих линий электромагнитных волн.

Т-волны могут существовать только в двухсвязных или многосвязных линиях передачи (причем как в открытых линиях, так и в волноводах).

Е- и Н-волны могут существовать в односвязных и многосвязных волноводах различного поперечного сечения.

Гибридные волны могут существовать в неоднородных линиях передачи различных типов.

2. МЕТОДЫ ИЗУЧЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ПРОЦЕССОВ В ЛИНИЯХ ПЕРЕДАЧИ

Так как энергия от генератора переносится к нагрузке электромагнитной волной, распространяющейся вдоль линии, то наиболее общим методом изучения процессов в линиях передачи является метод электродинамики, основанный на решении волновых уравнений для векторов E и H с последующим определением передаваемой мощности как потока вектора Пойнтинга через поперечное сечение линии.

В то же время в линиях передачи с Т-волной, где понятия ток в проводниках линии и напряжение между ними имеют вполне конкретный физический смысл, наряду с методами электродинамики можно воспользоваться для описания протекающих в этих линиях электромагнитных процессов методами теории цепей с распределенными параметрами (теорией длинных линий), основанными на решении телеграфных уравнений для токов и напряжений с последующим определением передаваемой мощности как произведения тока и напряжения в нагрузке линии.

5

Оба эти метода для линий передачи с Т-волной приводят к одинаковым результатам. Однако метод теории цепей связан с использованием более простого математического аппарата и был первым исторически. Его и применяют в инженерной практике при расчете характеристик этих линий.

В линиях передачи с Е- и Н-волнами из-за наличия продольных составляющих векторов E и H понятие напряжения теряет свой физический смысл, поэтому описание протекающих в них электромагнитных процессов возможно только методами электродинамики. Эти методы и будут рассмотрены в настоящем пособии.

3. ОБЩИЕ СВОЙСТВА НАПРАВЛЯЕМЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

3.1. Постановка задачи и порядок ее решения

Постановка задачи и допущения. Пусть имеется бесконечно длинная однородная линия передачи. Предположим, что металлические части линии выполнены из идеального проводника (γ м = ∞ ), а диэлектрические части и окружающая среда являются идеальными диэлектриками (γ д = 0). Кроме того, будем считать что в рассматриваемой области отсутствуют сторонние токи и заряды.

Требуется определить электромагнитное поле, которое может существовать в данной линии передачи при условии, что это поле гармоническое во времени, а частота колебаний равна ω .

Предположение о виде решения. Поле в линии будем искать в виде суммы (суперпозиции) Е- и Н-волн, распространяющихся вдоль оси 0z, совпадающей с продольной осью рассматриваемой линии передачи (заметим, что Т-волны являются частным случаем Е- и Н-волн).

Решение. Искомое поле должно удовлетворять однородным уравнениям Максвелла в комплексной форме:

6

и граничному условию для касательной. составляющей вектора напряженности электрического поля ( Ε τ ) на поверхностях идеальных проводников:

где k = ω ε аµа – волновое число для плоской однородной волны, распространяющейся в безграничной среде с параметрами диэлектрика, заполняющего (окружающего) линию передачи. В дальнейшем такую среду для краткости будем именовать «свободным пространством».

При решении задачи определения структуры электромагнитных полей Е- и Н-волн в линиях передачи используется следующий прием:

все поперечные составляющие векторов поля выражают c помощью так называемых «уравнений связи» через имеющиеся в данной волне продольные составляющие. векторов.напряженности электрического или магнитного поля ( Ε z для Е-волн и Η z для Н-волн);

решают волновые уравнения только для этих продольных составляющих;

вычисляют с помощью уравнений связи поперечные составляющие

векторов E и H в линии передачи.

Таким образом, решение задачи сводится к составлению уравнений связи и решению одномерных однородных волновых уравнений для продольных составляющих векторов E или H . Для Е-волн предстоит ре-

Постоянные коэффициенты, которые получаются при интегрировании этих уравнений, определяются при наложении на полученные решения граничного условия (2).

3.2. Уравнения связи для Е- и Н-волн

Уравнения связи получаются в результате преобразования уравнений Максвелла (1), раскрытых для соответствующей системы координат.

7

Для декартовой (прямоугольной) системы координат (x,y,z) уравнения связи для Е- и Н-волн выглядят следующим образом:

Е-волны

где K – волновое число для E и H-волн в волноводе.

Для цилиндрической системы координат (ρ ,ϕ ,z) уравнения связи для Е- и Н-волн выглядят следующим образом:

Е-волны

8

3.3. Решение волновых уравнений для продольных составляющих векторов напряженности

электрического и магнитного поля Е- и Н-волн

Решение волновых уравнений будем искать в обобщенно-цилиндри- ческой ортогональной системе координат (ξ ,η ,z), частными случаями которой являются декартова (прямоугольная) система координат (x,y,z) и цилиндрическая система координат (ρ ,ϕ ,z). Координатная линия 0z во всех этих системах представляет собой прямую, перпендикулярную плоскости, в которой расположены две другие координатные линии (эти линии для декартовой системы координат представляют собой две взаимно перпендикулярные прямые, а для цилиндрической системы координат – радиус-вектор и дугу окружности).

Так как волновые уравнения (4) и (5) абсолютно идентичны, то в настоящем подразделе мы будем интегрировать однородное волновое уравнение для скалярной функции Ω (ξ ,η ,z), помня о том, что полученное решение в одинаковой мере удовлетворит уравнениям (4) и (5).

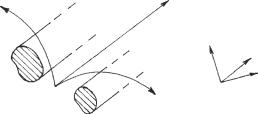
Ориентируем систему координат (ξ ,η ,z) таким образом, чтобы ось 0z совпала с продольной осью линии передачи, т.е. с направлением движения фазового фронта электромагнитной волны, распространяющейся вдоль данной линии (рис. 2). В этом случае оператор Лапласа 2

где 2 (ξ , η ) – оператор Лапласа по поперечным координатам (поперечный лапласиан).

Рис. 2. Ориентировка обобщенно-цилиндрической системы координат относительно линии передачи

9

При выбранной ориентации обобщенно-цилиндрической системы координат относительно линии передачи исходное волновое уравнение для функции Ω (ξ ,η ,z) примет следующий вид:

Решение этого уравнения будем искать методом разделения переменных (методом Фурье). В соответствии с идеей метода, искомую функцию Ω (ξ ,η ,z) представим в виде произведения двух функций, одна. из которых (Ψ (ξ ,η )) зависит только от переменных ξ и η , а вторая ( Ζ (z)) – только от переменной z. В этом случае

Поделив. почленно обе части этого уравнения на произведение Ψ (ξ ,η ) Ζ (z) и перейдя во втором. члене от частного дифференциала к полному (так как функция Ζ (z) зависит только от одной переменной), получим

В этом уравнении первый член зависит только от переменных ξ и η , второй – только от переменой z, а их сумма равна постоянной величине −k2. Уравнение (15) должно быть справедливым при любом значении переменной z. Очевидно, что это требование может быть удовлетворено только в том случае, если и первый, и второй члены этого уравнения порознь равны неким постоянным величинам. Обозначим эти постоянные – æ2 и – K2 соответственно. Тогда уравнение (15) может быть представлено в виде системы из трех уравнений:

10