
Демин - Сопротивление материалов, 2006
.pdf
Pв = P cos α =1,2 0,707 = 0,849 кН;
Pг = P sin α =1,2 0,707 = 0,849 кН.
2) Запишем выражения для внутренних сил в произвольном сечении:
Q(ϕ) = Pг cos ϕ− Pв sin ϕ; N (ϕ) = Pг sin ϕ+ Pв cos ϕ;
M (ϕ) = Pгr sin ϕ− Pвr (1−cos ϕ);
Q(ϕ) = 0,849 cos ϕ−0,849sin ϕ;
N (ϕ) = 0,849 sin ϕ+0,849 cos ϕ;
M (ϕ) = 0,136 sin ϕ−0,136 (1−cos ϕ).
Полученные формулы используем для вычисления Q, N, M (табл. 9.2) с шагом угла δϕ = 30°.
Таблица 9.2
Величина |
ϕ = 0 |
ϕ = 30 |
ϕ = 60 |
ϕ = 90 |
ϕ = 120 |
ϕ = 150 |
ϕ = 180 |
Q, кН |
0,849 |
0,311 |
–0,311 |
–0,849 |
–1,16 |
–1,16 |
–0,849 |
N, кН |
0,849 |
1,16 |
1,16 |
0,849 |
0,31 |
–0,31 |
–0,849 |
M, кН м |
0 |
0,0497 |
0,0497 |
0 |
–0,086 |
–0,186 |
–0,272 |
По данным табл. 9.2 строим эпюры Q, N и М (рис. 9.4). |
|
||||||
|
|
0,311 |
0,849 |
1,16 |
|
|
|
|
|
|
|
|
|
||
|
0,311 |
|
|
|
1,16 |
|
|
|
|
|
|
|
|
|
|
0,849 |
|
|
|
|
0,849 |
|
|
|
|
Эпюра Q, кН |
|
|
|
||
1,16 0,849
0,311
1,16
0,311
0,849 |
0,849 |
Эпюра N, кН
0,086
0,0497
0,186
0,0497
0,272
Эпюра M, кН м
Рис. 9.4

3) Определим напряжения в опасном сечении (рис. 9.5) при следую- |
|||||
щих значениях внутренних усилий: M = –272 Н м; N = –849 Н. |
|
||||
|
b1 |
= 3 |
Эпюра σ, МПа |
|
|
|
|
|
9,959 |
||
rн = 19,333 |
с = 0,178 |
|
|
|
|
|
|
|
|
h = 6 |
|
|
a = 2,667 |
Ц.Т. |
|
|
|
|
|
0,304 |
|
||
r = 16 |
|
|
-0,326 |
|
|
r0 = 15,822 |
|
|
|
||
|
|
|
|
||
|
rв = 13,333 |
|
-10,896 |
|
|
|
b2 = 6 |
|
|
|
|
|
Нейтральная линия при N = 0 |
|
|
||
|
Ось кривизны |
|
|
|
|
Рис. 9.5
Нормальные напряжения вычисляются по формуле:
|
N |
|
M |
ρ−ρ |
0 |
|
|
σ = |
|
± |
|
|
|
. |
|
|
|
|
|
||||
|
A |
|
|
|
ρ |
|
|
|
|
Ac |
|
|
|||
Центр тяжести трапеции находится от основания на расстоянии:
|
2b |
+b |
2 |
h |
|
2 3 +6 |
6 |
|
||
а = |
1 |
|
|
|
= |
|
|
|
= 2,667 см; |
|
b +b |
|
3 |
3 +6 |
3 |
||||||
|
|
|
|
|
|
|||||
|
1 |
2 |
|
|
|
|
|
|
|
|
Внутренний и наружный радиусы криволинейного стержня rв = r − a =16 − 2,667 =13,333 см;
rн = r + h − a =16 + 6 − 2,667 =19,333 см.
Радиус кривизны нейтрального слоя для сечения в форме трапеции
(при N = 0):
|
|
|
|
|
(b |
+ b |
|
) h2 |
|
|
|
|
|||
|
|
|
r0 |
= |
1 |
|
2 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
rн |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
− (b2 |
−b1) h |
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 (rнb2 − rвb1) ln |
r |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
в |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r0 |
= |
|
|
|
(3 + 6)62 |
|
|
|
|
|
|
|
|
=15,822 см. |
|
|
|
|
|
19,333 |
|
|
|||||||||
|
2 |
(19,333 6 −13,333 3) ln |
|
|
|
|
|
|
|
−(6 −3) 6 |
|
||||
|
13,333 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Расстояние от центра тяжести до нейтрального слоя (при N = 0)
c = r − r0 =16 −15,822 = 0,178 см.
Площадь сечения
|
|
|
А = (b + b )h / 2 = (6 + 3)6 / 2 = 27 см2. |
|
||||
|
|
|
1 |
2 |
|
|
|
|
Значения напряжений в характерных точках |
|
|||||||
ρ = rн =19,333 см; |
|
|
|
|
|
|||
|
879 |
|
27200 |
|
19,333 −15,822 |
|
= 995,9 Н/см2 |
|
σ = − |
|
+ |
|
|
|
|
= 9,959 МПа; |
|
|
|
|
||||||
|
27 |
|
27 0,178 |
|
19,333 |
|
|
|
|
|
|
|
|
|
|||
ρ = r =16 см; |
|
|
|
|
|
|
|
|
|
879 |
|
27200 |
16 −15,822 |
|
= 30,4 Н/см2 |
|
|
σ = − |
|
+ |
|
|
|
|
= 0,304 МПа; |
|
|
|
|
||||||
|
27 |
|
27 0,178 |
|
19,333 |
|
|
|
|
|
|
|
|
|
|||

ρ = r0 =15,822 см; |
|
|
|
|
|
|||
|
879 |
|
27200 |
15,822 −15,822 |
|
= −32,6 Н/см2 |
|
|
σ = − |
|
+ |
|
|
|
|
= −0,326 МПа; |
|
|
|
|
||||||
|
27 |
|
27 0,178 |
|
19,333 |
|
|
|
|
|
|
|
|
|
|||
ρ = rв =13,333 см; |
|
|
|
|
|
|||
|
879 |
|
27200 |
13,333 −15,822 |
|
2 |
|
|
σ = − |
|
+ |
|
|
|
= −1089,6 Н/см |
|
= −10,896 МПа. |
27 |
27 0,178 |
19,333 |
|
|||||
|
|
|
|
|
|
|||
По полученным значениям строим эпюру σ (рис. 9.5).
Контрольная работа 4
Задача 10 РАСЧЕТ СТЕРЖНЯ НА УСТОЙЧИВОСТЬ
Задание. Стальной стержень (рис. 10.1) сжимается силой Р. Требуется: 1) найти размеры поперечного сечения (рис. 10.2) при расчетном сопротивлении на простое сжатие R = 210 МПа; 2) найти значение критической силы и коэффициент запаса устойчивости. Данные взять из табл. 10.1.
Таблица 10.1
№строки |
Схема закрепления- |
Сечение стержняпо |
Р, кН |
A, м |
стержня по рис. 10.1 |
рис. 10.2 |
|||
1 |
1 |
1 |
100 |
2,1 |
2 |
2 |
2 |
200 |
2,2 |
3 |
3 |
3 |
300 |
2,3 |
4 |
4 |
1 |
400 |
2,4 |
5 |
5 |
2 |
500 |
2,5 |
6 |
1 |
3 |
600 |
2,6 |
7 |
2 |
1 |
700 |
2,7 |
8 |
3 |
2 |
800 |
2,8 |
9 |
4 |
3 |
900 |
2,9 |
0 |
5 |
1 |
50 |
3,0 |
|
е |
а |
в |
г |
P P
P
1 |
A |
2 |
A |
|
|
P |
|
P |
P |
|
3 |
A |
4 |
5 |
A |
|
||||
|
A |
|
A |
|
|
|
|
||
Рис. 10.1 |
|
|
|
|
1 |
a |
2 |
a |
3 |
2a |
|
6a |
6a |
4a |
||||
|
|
|
||||
|
a |
|
a |
|
2a |
|
a 4a a |
|
2a 4a 2a |
|
|
a 4a a |
|
|
|
Рис. 10.2 |
|
|
|
P |
|
y |
|
Пример 1 0 : |
Стальной |
стер- |
|
|
|
|
|
жень (рис. 10.3) сжимается силой Р = |
|||
|
A |
x |
2a |
400 кН. Найти размеры поперечного се- |
|||
|
|
чения, значение критической силы и ко- |
|||||
|
|
|
|
эффициент запаса устойчивости, |
если |
||
|
|
a |
|
l = 2 м, |
R = 200 МПа. |
|
|
|
Рис. 10.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Р е ш е н и е:
1) Для поперечного сечения определяем площадь А в общем виде и выражаем размер а через площадь А:
A = a 2a = 2a2 ;
a = |
A |
= 0,707 A . |
|
2 |
|
2) Минимальный момент инерции сечения
I y = Imin = 2a12(a)3 = 0,167a4 . 3) Минимальный радиус инерции сечения
i = |
I |
min = |
0,167a4 |
= 0,289a . |
min |
|
A |
2a2 |
|
|
|
|
4) Гибкость стержня
λ = |
µl |
= |
1 2 |
= |
6,921 |
. |
|
0,289a |
|
||||
|
imin |
|
a |
|||
5) Первое приближение ϕн1 = 0,5 :
A = |
P |
= |
400 103 |
= 4 10 |
−3 |
м |
2 |
; |
ϕн1R |
0,5 200 106 |
|
|
|||||
|
|
|
|
|
|
|
a = 0,707 A = 0,707
A = 0,707  4 10−3 = 0,045 м;
4 10−3 = 0,045 м;
λ = 6,921a = 06,,045921 =155.
Для найденной гибкости определяем соответствующий коэффициент продольного изгиба, используя линейную интерполяцию табличных значений:
λ=150 ; ϕ = 0,328 ;
λ=160 ; ϕ = 0,290 ;
ϕк = 0,290 + (160 −155) |
0,328 − 0,290 |
= 0,309. |
1 |
10 |
|
|
|
Вычисляем действующее и допускаемое напряжения:
P |
= |
400 10−3 |
=100 МПа; |
|
A |
4 10−3 |
|||
|
|
Rсжϕк1 = 200 0,309 = 61,8 МПа;
∆ = 100 − 61,8 100 % = 62 % > 5 % . 61,8
Получили перегрузку, величина которой больше 5 %, следовательно, выполняем второе приближение.
6) Второе приближение
ϕн |
= (ϕн |
+ ϕк |
) / 2 = (0,5 + 0,309) / 2 = 0,405 ; |
||||
2 |
|
1 |
|
|
1 |
|
|
A = |
P |
|
= |
|
400 103 |
= 4,94 10−3 м2; |
|
|
|
0,405 200 106 |
|||||
|
|
ϕн2R |
|
||||

a= 0,707 A = 0,707
A = 0,707  4,94 10−3 = 0,05 м;
4,94 10−3 = 0,05 м;
λ= 6,921a = 60,,92105 =138,4 ;
λ=130 ; ϕ = 0,425 ;
λ=140 ; ϕ = 0,376 ;
ϕк = 0,376 + (140 −138,4) |
0,425 − 0,376 |
= 0,384 ; |
||||
2 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
P |
= |
400 10−3 |
= 80,1 МПа; |
|
|
|
A |
4,94 10−3 |
|
|||
|
|
|
|
|
||
Rсжϕк1 = 200 0,384 = 76,8 МПа;
∆ = 80,1 − 76,8 100 % = 4,3 % < 5 % . 61,8
Во втором приближении также имеет место перегрузка, но ее величина стала меньше 5 %. Принимаем: a = 5 cм; λ =138,4 .
7) Находим критическую силу. Так как λ =138,4 > λпр =100 , расчет ведем по формуле Эйлера:
|
|
Imin = 0,167a4 = 0,167 54 =104 см4; |
||||
P |
= |
π2EImin |
= |
3,142 2 108 104 10−8 |
= 604 кН. |
|
(1 2)2 |
||||||
кр |
|
(µl)2 |
|
|
||
8) Определяем коэффициент запаса
kуст = PPкр = 604400 =1,51.
Задача 11 РАСЧЕТ БАЛКИ НА УДАРНУЮ НАГРУЗКУ
Задание. На двутавровую балку, свободно лежащую на двух жестких опорах (рис. 11.1), с высоты h падает груз Q. Требуется: 1) найти наибольшее нормальное напряжение в балке; 2) решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой (т.е. осадка от груза 1 кН) равна α; 3) сравнить полученные результаты. Данные взять из табл. 11.1.
|
|
|
|
|
|
Таблица 11.1 |
||
|
|
|
|
|
|
|
|
|
№ строки |
№ схемы |
№ двутавра |
A, м |
Q, Н |
h, см |
|
α, м/кН |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
20 |
2,1 |
1100 |
11 |
|
21 10-3 |
|
2 |
2 |
20а |
2,2 |
1200 |
12 |
|
22 10-3 |
|
3 |
3 |
24 |
2,3 |
300 |
3 |
|
23 10-3 |
|
4 |
4 |
24а |
2,4 |
400 |
4 |
|
24 10-3 |
|
5 |
1 |
27 |
2,5 |
500 |
5 |
|
25 10-3 |
|
6 |
2 |
27а |
2,6 |
600 |
6 |
|
26 10-3 |
|
7 |
3 |
30 |
2,7 |
700 |
7 |
|
27 10-3 |
|
8 |
4 |
30а |
2,8 |
800 |
8 |
|
28 10-3 |
|
9 |
1 |
33 |
2,9 |
900 |
9 |
|
29 10-3 |
|
0 |
2 |
36 |
3,0 |
1000 |
10 |
|
30 10-3 |
|

|
е |
|
д |
|
в |
а |
г |
б |
h |
Q |
|
|
1 |
2 |
h |
Q |
|
0,25A |
|
0,75A |
|
|
|
0,5A |
0,5A |
|
|
|
h |
Q |
3 |
4 |
|
h |
Q |
|
0,75A |
|
0,25A |
|
|
A |
A/ 3 |
|
Рис. 11.1
Методические указания
При наличии упомянутой в п. 2 пружины ∆ст = ∆б +β∆пр , где ∆б –
прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы); ∆пр − осадка пружины от
реакции, возникающей от силы Q; β – коэффициент, устанавливающий за-
висимость между осадкой пружины и перемещением точки приложения силы Q , вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого (коэффициент β находят из подобия треуголь-
ников).
Пример 1 1 : На двутавровую балку (№24, Wx = 289 см3, Ix = 3460 см4, l = 4 м), свободно лежащую на двух жестких опорах (рис. 11.2), с высоты h = 11 см падает груз Q = 600 Н. Найти наибольшее нормальное напряжение в балке; решить аналогичную задачу при условии, что правая опора за-
менена пружиной, податливость которой равна α = 25 10−3 м/кН.
|
|
|
h = 11 см |
|
|
|
Q = 600 Н |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0,75A |
|
|
|
0,25A |
|
|
|
|
||
|
|
|
Рис. 11.2 |
|
|
|
|
|
|
|
|
||
Р е ш е н и е: |
|
|
|
|
|
|
|
|
|||||
1) |
Определим прогиб балки в точке удара (в точке С) |
при статиче- |
|||||||||||
ском действии силы Q. Предварительно покажем единичное состояние, по- |
|||||||||||||
|
|
|
|
и вычислим перемещение δ от |
|||||||||
строим эпюру изгибающих моментов M |
|||||||||||||
единичной силы по формуле трапеций: |
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
1 |
|
|
3 |
|
|
|
A |
4 |
|
|
|
C |
|
B |
4 |
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
0,75A |
|
0,25A |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Эпюра |
|
|
||
|
|
|
|
|
|
|
|
|
M |
||||
|
|
|
|
|
|
|
3 |
A |
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 11.3 |
|
|
|
|
|
|
|
|
||

|
0,75l |
|
3 |
|
3 |
|
|
0,25l |
|
3 |
|
3 |
|
|
0,01172l3 |
|
|||
δ = |
|
0 |
+2 |
|
l |
|
l +0 +0 |
+ |
|
|
2 |
|
l |
|
l +0 +0 +0 |
= |
|
; |
|
6EI |
16 |
16 |
6EI |
16 |
16 |
EI |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∆ст = δQ = |
|
|
0,01172 43 |
|
600 = 6,50 10−5 м = 0,0065 см. |
||||||
|
|
1011 3460 10−8 |
||||||||||
|
2 |
|
|
|
||||||||
2) |
Определим динамический коэффициент: |
|||||||||||
|
kд =1+ 1+ |
2h |
=1+ |
1+ 2 11 =59,2 . |
||||||||
|
|
|
|
|
|
|
∆ст |
|
|
0,0065 |
||
3) |
Вычислим наибольшие нормальные напряжения в балке при ста- |
|||||||||||
тическом нагружении: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
max Q |
|
3 4 600 10−6 |
|
|||
|
σст = |
M |
= |
=1,56 МПа. |
||||||||
|
|
|
W |
16 289 |
10−6 |
|||||||
|
|
|
|
|
|
|
|
|||||
4) Наибольшие нормальные напряжения в балке при ударе
σд = kдσcт= 59,2 1,56 = 92,2 МПа .
5) Определим напряжения в балке при ударе, если правая опора заменена пружиной (рис. 11.4). Предварительно рассмотрим статическое нагружение.
A |
150 Н |
C 600 Н B |
450 Н |
|
|
C1 |
|
|
0,75A |
0,25A |
|
|
|
Рис. 11.4 |
|
Осадка опоры В |
|
|
|
|
∆B = 25 10−3 0,45 =1125 10−3 = 0,01125 м =1,125 см. |
||
Перемещение точки С, вызванное осадкой опоры В:
CC1 =1,125 34 = 0,844 см.
Полное перемещение точки С (с учетом осадки опоры В и прогиба балки)
∆ст = 0,844 +0,0065 ≈ 0,85 см.
Динамический коэффициент
kд =1+  1+ 20,8511 = 6,18.
1+ 20,8511 = 6,18.
Наибольшие нормальные напряжения в балке при ударе
σд = kдσcт =1,56 6,18 = 9,64 МПа.

Вывод: после замены жесткой опоры пружиной напряжения в балке при ударе уменьшились в 92,2 / 9,64 = 9,56 раз.
Задача 12 СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
Задание. Для балки, изображенной на рис. 12.1, требуется: 1) построить эпюры Q и M; 2) выполнить статическую и кинематическую проверку; 3) подобрать двутавровое сечение. Данные взять из табл. 5.1. При-
нять EJ = const.
q |
|
P |
q |
|
P |
|
|
1 |
2 |
|
|
a |
b |
c |
a |
b |
c |
|
q |
P |
|
q |
P |
|
|
3 |
4 |
|
|
a |
b |
c |
a |
b |
c |
q |
|
M |
q |
|
M |
|
|
5 |
6 |
|
|
a |
b |
c |
a |
b |
c |
|
q |
M |
8 |
q |
M |
|
|
7 |
|
|
|
a |
b |
c |
a |
b |
c |
|
|
q M |
|
|
q M |
|
P b |
9 |
0 |
|
|
a |
c |
aP |
b |
c |
|
|
|
Рис. 12.1 |
|
|
|
Методические указания
При решении задачи использовать метод сил. Для вычисления перемещений применять формулы сокращенного умножения эпюр.
Пример 1 2 : Для балки (рис. 12.2) построить эпюры поперечных сил Q и изгибающих моментов M; 2) выполнить статическую и кинематическую проверку; 3) подобрать двутавровое сечение. Допускаемое напряжение [σ]= 90 МПа.
Р = 20 кН q = 16 кН/м  M = 14 кН м
M = 14 кН м
A T |
B |
|
C |
|
|
|
D |
1,5 м |
3,2 м |
3,8 м |
1,8 м |
Рис. 12.2
Р е ш е н и е:
1)Находим степень статической неопределимости (число опорных связей минус три) n = 4 – 3 = 1.
2)Выбираем основную систему в виде балки на двух шарнирных опорах (рис. 12.3).
A 
 C
C
Рис. 12.3
3)Показываем эквивалентную систему (рис. 12.4).
Р= 20 кН q = 16 кН/м  M = 14 кН м
M = 14 кН м
A |
T |
|
B |
C |
∆B = 0 . |
|
|
|
X1 |
||
RA |
|
|
D |
|
|
1,5 м |
3,2 м |
3,8 м |
1,8 м RC |
|
|
|
|
|
Рис. 12.4 |
|
|
4) Составляем каноническое уравнение по методу сил:

∆B = δ11 X1 + ∆1p = 0.
5)Для определения перемещений δ11 и ∆1p предварительно постро-
им эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии. Перемещения будем искать по формулам перемножения эпюр. Для участков с распределенной нагрузкой необходимо знать моменты на концах и в серединах участков, для участков без распределенной нагрузки достаточно вычислить моменты на концах. Рассмотрим единичное состояние (рис. 12.5, все размеры даны в метрах).
|
|
A |
T |
|
|
B |
1,9 |
|
1,9 |
0,9 |
0,9 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
K |
D |
|
R |
|||||||
|
|
|
|
|
|
|
|
|
X1=1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
1,5 |
3,2 |
|
|
|
|
|
|
3,8 |
|
|
1,8 |
|
|
C |
|||||
|
R |
A |
|
|
|
|
|
|
|
|
R |
|||||||||||
|
|
|
|
4,7 |
|
|
|
|
|
|
5,6 |
|
|
|
|
|
|
|
||||
|
|
|
|
2, 555 |
1,688 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0,816 |
|
|
|
|
|
|
0,821 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,411 Эпюра M , м |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
A |
T |
|
|
B |
|
|
|
|
K |
D |
R |
C |
||||||||
Определяем реакции опор: |
|
Рис. 12.5 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∑M A = 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4,7 |
|
|
1 −10,3 |
|
c |
= 0 ; |
|
|
|
|
|
|
|
|||||
|
|
|
|
X |
R |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
__ |
|
1 4,7 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
R = |
= 0,4563 ; |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
C |
10,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∑MC = 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
__ |
|
__ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
10,3 RA −5,6 X1 |
= 0 ; |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
A = |
1 5,6 |
|
= 0,5437 . |
|
|
|
|
|
|
|
||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
10,3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверка:
∑y = 0 ;
−RA + X1 − RC = 0 ; –0,5437 + 1 – 0,4563 = 1 – 1 = 0.
Реакции опор найдены верно.
Вычисляем значения M1 в сечениях балки:
т. A: M1 = 0 ;
т. T: M1 = −1,5RA = −1,5 0,5437 = −0,816 м;
т. B: M1 = −(1,5 +3,2)RA = −(1,5 +3,3) 0,5437 = −2,555 м; т. K: M1 = −(1,9 +1,8)RC = −(1,9 +1,8) 0,4563 = −1,688 м; т. D: M1 = −1,8RC = −1,8 0,4563 = −0,821м;
т. R: M1 = −0,9RC = −0,0 0,4563 = −0,411м; т. C: M1 = 0 .
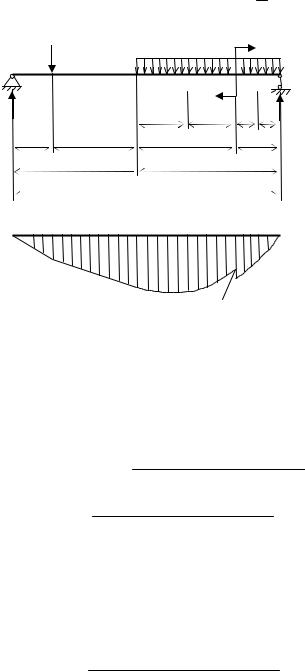
По найденным значениям строим эпюру M1 |
(рис. 12.5). |
||||||
Рассмотрим грузовое состояние основной системы (рис. 12.6). |
|||||||
|
Р = 20 кН |
q = 16 кН/м |
|
M = 14 кН м |
|||
A |
T |
B |
|
|
|
C |
|
|
|
|
K |
D |
R |
|
|
RA |
|
1,9 |
1,9 |
0,9 |
0,9 |
RC |
|
1,5 |
3,2 |
|
3,8 |
1,8 |
|
|
|
|
4,7 |
|
5,6 |
|
|
|
|
|
|
10,3 |
|
|
|
|
|
A |
T |
B |
K |
D |
R |
C |
Эпюра M P , кН м |
60,128 |
|
|
|
56,083 |
|
||
|
|
99,206 |
|
|
|||
|
124,402 |
|
|
|
|||
|
133,684 |
85,206 |
|
|
|
||
|
|
|
|
|
|
||
Рис. 12.6
Определяем реакции опор:
∑M A = 0 ;
−P 1,5 −q 5.6 (4,7 +5,6 / 2) − M + RC 10,3 = 0 ;
R = P 1,5 + q 5,6 (4,7 +5,6 / 2) + M ;
C |
10,3 |
|
RC = 20 1,5 +16 5,6 (4,7 +5,6 / 2) +14 = 69,515 кН; 10,3
∑MС = 0 ; |
|
|
|
|
−RA 10,3 |
+ P (3,2 +5,6) + q 5,6 (5,6 / 2) − M = 0 ; |
|||
RA = |
|
P (3,2 +5,6) + q 5,6 (5,6 / 2) − M |
; |
|
10,3 |
||||
|
|
|||
= 20 (3,2 +5,6) +16 5,6 (5,6 / 2) −14 =
RA 40,085 кН. 10,3
Проверка:
∑y = 0 ;
∑y =RA − P −q 5,6 + RC ;
40,085 − 20 −16 5,6 + 69,515 =109,6 −109,6 = 0 .
Реакции опор найдены верно.
Вычисляем значения моментов Mp в сечениях.
т. A: M p = 0 ;
т. T: M p = RA 1,5 = 40,085 1,5 = 60,128 кН м;
т. B: M p = RA 4,7 − P 3,2 = 40,085 4,7 −20 3,2 =124,402 кН м;
т. K: M p = RA (4,7 +1,9) − P (3,2 +1,9) −q 1,92 / 2 ;
т. K: M p = 40,085 (4,7 +1,9) − 20 (3,2 +1,9) −16 1,92 / 2 =133,684 кН м;
