
Основы Теории Цепей
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
141 |
|
|
|
A& |
= |
I& |
|
|
= |
|
|
|
I& |
|
|
|
=1 + |
Z& |
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
1 |
|
|
|
b |
. |
||||
& |
|
|
|
|
& |
& |
|
|
|
& |
|||||
22 |
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
I2 |
|
U&2 =0 |
& |
|
ZbZc |
|
|
|
Zc |
||||
|
|
|
|
& |
|
|
|||||||||
|
|
|
|
|
|
I1 |
& |
& |
|
|
|
|
|||
|
|
|
|
|
|
|
|
Zb |
+ Zc |
|
Zb |
|
|
|
|
Характеристические параметры Т-образного четырехполюсника:
Z& |
= |
A& |
A& |
= |
|
Z& |
a |
+ Z& |
c |
|
(Z& |
Z& |
+ Z& |
Z& |
+ Z& |
Z& |
) , |
||||||
11 12 |
|
|
|
|
|
|
|
||||||||||||||||
& & |
|
& |
|
& |
|
|
|||||||||||||||||
1C |
|
|
|
|
|
|
|
a |
b |
c |
b |
a |
c |
|
|||||||||
|
|
A A |
|
|
Z |
b |
+ Z |
c |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
21 |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z&2C = |
|
A& |
A& |
= |
|
|
Z& |
|
+ Z& |
|
|
(Z&a Z&b + Z&c Z&b + Z&a Z&c ) , |
|||||||||||
|
22 12 |
|
|
|
b |
|
c |
||||||||||||||||
& & |
|
|
|
& |
|
& |
|||||||||||||||||
|
|
|
A A |
|
|
|
Z |
a |
+ Z |
c |
|
|
|
|
|
|
|
||||||
|
|
21 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
& & |
|
|
|
|
|
|
|
|
(Z&a + Z&c )(Z&b + Z&c ) |
||||||||||
g = Arch |
A11 A22 |
= Arch |
|
|
|
|
|
|
|
|
. |
||||||||||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z& |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|||
Для симметричного Т-образного четырехполюсника ( Z&a = Z&b ,
A& |
= A& |
|
): |
|
|
|
|
|
|
|
|
11 |
22 |
|
|
|
|
|
|
|
|
|
|
& |
& |
|
& |
= |
& |
& |
& |
& |
|
(Z&a + Z&c ) |
|
|
|
& |
|||||||||
Z1C |
= Z |
2C = ZT |
Za |
(Za |
+ 2Zc ) , |
g = Arch |
. |
||||
|
|
|
|
|
|
|
|
|
|
Zc |
|
Расчетные формулы для Г-образных схем могут быть получены из формул для Т-образного четырехполюсника, если принять
Z&b = 0 (соответствует рис.88, а), или Z&a = 0 (для схемы рис.88, б).
Применяя подобную методику, можно получить расчетные формулы и для П-образного четырехполюсника.
Возможно решение обратной задачи: по заданным параметрам четырехполюсника (первичным или характеристическим) найти
значения Z&a , Z&b , Z&c для схемы Т- или П-образного четырехпо-
люсника. Отсюда следует, что любой пассивный линейный четырехполюсник, для которого известны первичные или характеристические параметры, может быть заменен Т- или П-образной схемой.
Схемы замещения четырехполюсника
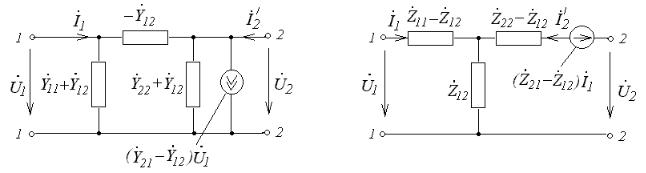
142
В радиотехнике для упрощения анализа и расчета электронных схем, содержащих активные элементы (транзисторы, микросхемы, лампы и т. д.) используются схемы замещения, которые строятся на основании систем уравнений четырехполюсника. На практике чаще всего применяют П- и Т-образную схему замещения (рис.89).
а |
б |
Рис.89
В соответствии с первым законом Кирхгофа для входного узла схемы
(рис.89, а):
I&1 = (Y&11 +Y&12 )U&1 + (−Y&12 )(U&1 −U&2 ) =Y&11U&1 +Y&12U&2 .
Для выходного узла:
I&2′ = (Y&22 +Y&12 )U&2 + (−Y&12 )(U&2 −U&1 ) + (Y&21 −Y&12 )U&1 =Y&21U&1 +Y&22U&2 .
Таким образом, для схемы (рис.89, а) справедлива система урав-
нений в Y& −параметрах. Зависимый источник тока сохраняется только в случае необратимого четырехполюсника. Для обратимого
четырехполюсника Y&21 =Y&12 и источник тока отсутствует
(Y&21 −Y&12 )U&1 = 0, т. е. схема замещения представляет собой пас-
сивный П-образный четырехполюсник.
В соответствии со вторым законом Кирхгофа для входного контура схемы
(рис.89, б):
143
U&1 = (Z&11 − Z&12 )I&1 + Z&12 (I&2′ + I&1 ) = Z&11I&1 + Z&12 I&2′.
Аналогично для выходного контура:
U&2 = (Z&21 − Z&12 )I&1 + (Z&22 − Z&12 )I&2′ + Z&12 (I&2′ + I&1 ) = Z&21I&1 + Z&22 I&2′.
Как и в предыдущем случае, для схемы (рис.89, б) справедлива
система уравнений в Z& −параметрах. Зависимый источник напряжения сохраняется только в случае необратимого четырехполюс-
ника. Для обратимого четырехполюсника Z&21 = Z&12 и источник э.
д. с. отсутствует, т. е. схема замещения представляет собой пассивный Т-образный четырехполюсник.
Параметры схем замещения могут быть выражены через любую из систем параметров. Пассивный четырехполюсник в виде П- образной схемы замещения может быть преобразован в Т-образный четырехполюсник (и наоборот) по правилу преобразования треугольника сопротивлений в звезду и наоборот.
Лекция 17.
Сложные четырехполюсники
Сложным называется четырехполюсник, который может быть образован в результате соединения между собой нескольких, в частности двух, четырехполюсников. Параметры сложного четырехполюсника могут быть рассчитаны, если известны параметры каждого из составляющих четырехполюсников. В зависимости от схемы соединения четырехполюсников расчет параметров результирующего (эквивалентного) проводят, используя соответствующие уравнения в матричной форме.
1. Каскадное соединение четырехполюсников.
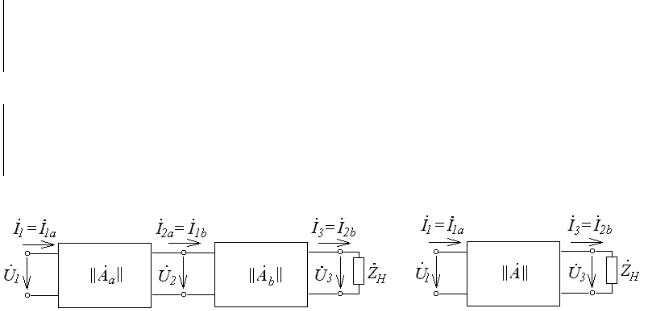
144
На практике четырехполюсники часто соединены каскадно, т. е. вход последующего соединяется с выходом предыдущего (рис.90,
а). Уравнения четырехполюсников в матричной форме 
 A&
A&
 имеют вид:
имеют вид:
|
|
U& |
|
|
|
|
= |
|
|
|
|
|
|
|
A& |
A& |
|
|
|
|
|
|
|
|
|
|
|
U& |
|
|
|
|
|
|
= |
|
|
|
|
A& |
|
|
|
|
|
|
U& |
|
|
|
|
|
; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
11 12 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
|
21 22 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
a |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
U& |
|
|
|
= |
|
|
|
|
|
|
|
A& |
A& |
|
|
|
|
|
|
|
|
|
|
U& |
|
|
|
|
|
|
= |
|
|
|
A& |
|
|
|
|
|
|
U& |
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
11 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
& |
& |
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
b |
|
|
|
|
21 |
22 |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
b |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
а |
б |
Рис.90
При каскадном соединении
U&1 =U&1a , U&2 =U&2a =U&1b , U&3 =U&2b ,
I& |
= I& |
, I& |
|
|
= I& |
, |
|
I& |
= I& |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
|
|
1a |
|
|
|
|
2a |
|
|
|
|
|
1b |
|
|
|
|
|
3 |
|
|
2b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
U&1 |
|
= |
|
A& |
|
|
|
|
|
|
|
A& |
|
|
|
|
|
|
|
U&2 |
|
|
|
|
= |
|
|
|
A& |
|
|
|
|
|
U&3 |
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
& |
|
|
|
|
a |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, матрица 
 A&
A&
 результирующего (рис.90, б) четы-
результирующего (рис.90, б) четы-
рехполюсника равна произведению матриц составляющих четырехполюсников:
145

 A&
A&
 =
= 
 A&a
A&a 


 A&b
A&b 
 .
.
В случае каскадного соединения большего числа четырехполюсников, матрица эквивалентного четырехполюсника получается последовательным перемножением матриц каскадов.
Если обеспечить согласование выхода первого каскада с входом второго
Z& |
= Z& |
, а также согласовать нагрузку с выходом второго кас- |
|||||||||||||
2Ca |
|
|
1Cb |
|
|
|
|
|
|
|
|
|
|
|
|
када Z& |
2Cb = Z&H , то выражения для напряжений на зажимах каска- |
||||||||||||||
дов примут следующий вид: |
|
|
|
|
|
|
|
||||||||
|
|
|
Z& |
|
|
g& |
|
Z& |
g& |
|
Z& |
g& |
|
+g& |
|
U&2 = |
|
|
1Cb |
U& |
3e |
b , U&1 = |
1Ca |
U&2e |
a и U&1 = |
1Ca |
U&3e |
a |
|
b . |
|
|
|
|
Z&2Ca |
Z&2Cb |
|
||||||||||
|
|
|
Z&2Cb |
|
|
|
|
|
|
|
|
||||
Аналогичные выражения получаются и для токов, протекающих через зажимы каскадов:
I& |
|
= I& |
= |
|
Z&2Cb |
I& eg&b , I& |
= I& |
= |
Z&2Ca |
I& |
eg&a |
и |
||
|
& |
|
||||||||||||
2a |
|
1b |
|
3 |
1 |
1a |
|
& 2a |
|
|
||||
|
|
|
|
|
|
Z |
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
1Cb |
|
|
|
|
1Ca |
|
|
|
I& |
= |
Z&2Cb |
I& eg&a +g&b . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
& |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1Ca |
|
|
|
|
|
|
|
|
|
|
|
Таким образом, каскадное согласованное соединение четырехполюсников можно заменить одним эквивалентным, имеющим харак-
теристические сопротивления равные входному Z&1Ca и выходному Z&2Cb , и постоянную передачи равную сумме постоянных передачи
каскадов g& = g&a + g&b , т. е. собственное затухание a = aa + ab и коэффициент фазы b = ba + bb .
В общем случае постоянная передачи каскадной схемы, составленной из согласованных линейных четырехполюсников, равна сумме постоянных передачи четырехполюсников, составляющих эту схему:
146
n
g&Э = aЭ + jbЭ = ∑g&i .
i=1
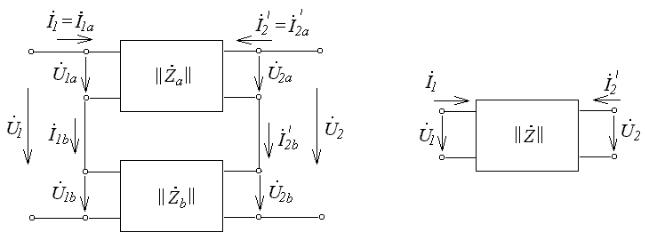
2. Последовательное соединение четырехполюсников.
Последовательным называется соединение четырехполюсников, при котором как входные, так и выходные зажимы соединены последовательно (рис.91). При последовательном соединении четырехполюсников удобно воспользоваться системой уравнений в Z−параметрах, так как матрица токов для составных четырехполюсников одинакова.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
||||||||
Рис.91 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
U& |
|
|
|
|
|
|
|
Z& |
Z& |
|
|
|
|
|
|
|
|
|
|
|
I& |
|
|
|
|
|
|
|
Z&a |
|
|
|
|
I& |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
= |
|
|
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
|
|
, |
||
|
|
U&2 |
|
|
|
a |
|
|
|
Z&21Z&22 |
|
|
|
|
|
|
a |
|
|
|
|
I&2′ |
|
|
|
|
|
a |
|
|
|
|
|
|
|
I&2′ |
|
|
|
|
a |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
U& |
|
|
|
|
|
|
|
Z& Z& |
|
|
|
|
|
|
|
|
I& |
|
|
|
|
|
Z&b |
|
|
|
|
|
I& |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
= |
|
11 |
12 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
|
. |
||||||||||
|
|
U&2 |
|
|
|
b |
|
|
|
Z&21Z&22 |
|
|
|
b |
|
|
|
|
I&2′ |
|
|
|
b |
|
|
|
|
|
|
|
I&2′ |
|
|
|
|
b |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Результирующие напряжения и токи на входе и выходе четырехполюсников:
U&1 =U&1a +U&1b , U&2 =U&2a +U&2b ,
147
I&1 = I&1a = I&1b , |
|
I&2′ = I&2′a = I&2′b . |
|||||||||||||||||||||||
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
U& |
|
= |
|
|
|
Z& |
|
|
+ |
|
Z& |
|
|
|
|
|
|
|
|
I& |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
|
U&2 |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
I&2′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
т. е. матрица сопротивлений эквивалентного четырехполюсника
(рис.91, б)

 Z&
Z&
 =
= 
 Z&a
Z&a 
 +
+ 
 Z&b
Z&b 
 .
.
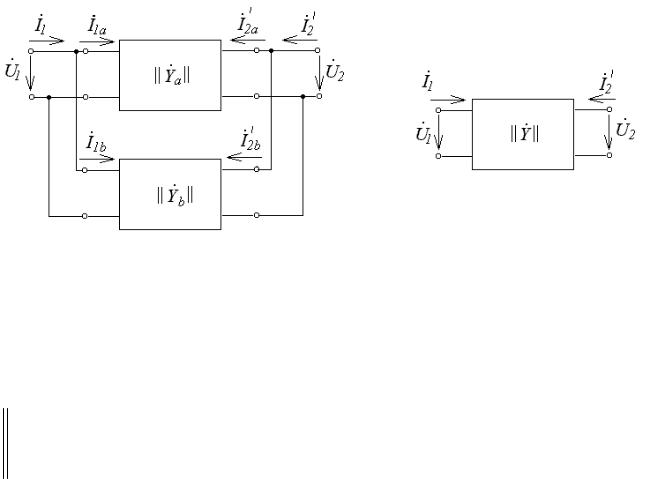
3. Параллельное соединение четырехполюсников.
При параллельном соединении как входные, так и выходные зажимы составляющих четырехполюсников соединяются параллель-
но (рис.92).
а |
б |
Рис.92
Запишем уравнения исходных четырехполюсников (рис.92, а) в системе Y−параметров:
I& |
|
|
|
|
= |
|
|
|
Y& Y& |
|
|
|
|
|
|
|
U& |
|
|
|
|
= |
|
Y& |
|
|
|
U& |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
11 12 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
I&2′ |
|
|
|
|
|
|
|
|
Y&21Y&22 |
|
|
|
|
|
|
|
U&2 |
|
|
|
|
|
|
a |
|
|
|
U&2 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
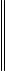
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
148 |
||||
I& |
|
|
|
|
= |
|
|
|
Y& Y& |
|
|
|
|
|
|
|
U& |
|
|
|
|
= |
|
Y& |
|
|
|
U& |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
11 12 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||||
I&2′ |
|
|
|
|
|
|
|
|
Y&21Y&22 |
|
|
|
|
|
|
|
U&2 |
|
|
|
|
|
|
b |
|
|
|
U&2 |
|
|
|
|
|
|
|
b |
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Напряжения и токи на входе и выходе эквивалентного четырехполюсника (рис.92, б):
U&1 =U&1a =U&1b , |
|
|
|
U&2 =U&2a =U&2b , |
||||||||||||||||||
|
|
I&1 = I&1a + I&1b , |
|
I&2′ = I&2′a + I&2′b . |
||||||||||||||||||
|
|
Следовательно, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
I& |
|
= |
|
Y& |
|
+ |
|
Y& |
|
|
|
|
|
|
|
U& |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
|
|
I&2′ |
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
U&2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Матрица проводимостей эквивалентного четырехполюсника
(рис.92, б)

 Y&
Y&
 =
= 
 Y&a
Y&a 
 +
+ 
 Y&b
Y&b 
 .
.
3.Последовательно-параллельное соединение четырехполюсников.
Вданном случае входные зажимы составляющих четырехполюсников соединяются последовательно, а выходные −параллельно
(рис.93).
149
а |
б |
Рис.93
Запишем систему уравнений четырехполюсников в Н−параметрах:
|
U& |
|
|
|
|
|
|
|
H& |
H& |
|
|
|
|
|
|
|
I& |
|
|
|
|
|
|
H&a |
|
|
|
I& |
|
|
|
|
|
|
|
|
U& |
|
|
|
|
|
|
H&b |
|
|
|
I& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
= |
|
|
|
11 |
12 |
|
|
|
|
|
|
|
1 |
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
, |
|
|
|
1 |
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
. |
|||
|
I&2′ |
|
|
|
a |
|
|
|
H&21H&22 |
|
|
|
a |
|
|
|
U&2 |
|
|
|
a |
|
|
|
|
|
|
U& |
2 |
|
|
|
a |
|
|
|
I&2′ |
|
|
|
b |
|
|
|
|
|
|
U& |
2 |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Для эквивалентного четырехполюсника (рис.93, б) выполняются соотношения:
U&1 =U&1a +U&1b , |
|
U&2 =U&2a =U&2b , |
||||||||||||||||||||||
|
I&1 = I&1a = I&1b , |
I&2′ = I&2′a + I&2′b . |
||||||||||||||||||||||
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
U& |
|
= |
|
|
|
H& |
|
|
+ |
|
H& |
|
|
|
|
|
|
|
I& |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
|
I&2′ |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
U& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
т. е. матрица Н−параметров эквивалентного четырехполюсника:

 H&
H& 
 =
= 
 H&a
H&a 
 +
+ 
 H&b
H&b 
 .
.
150
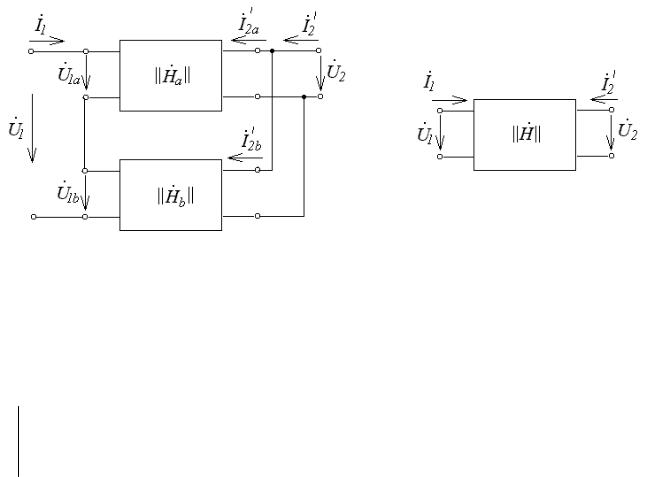
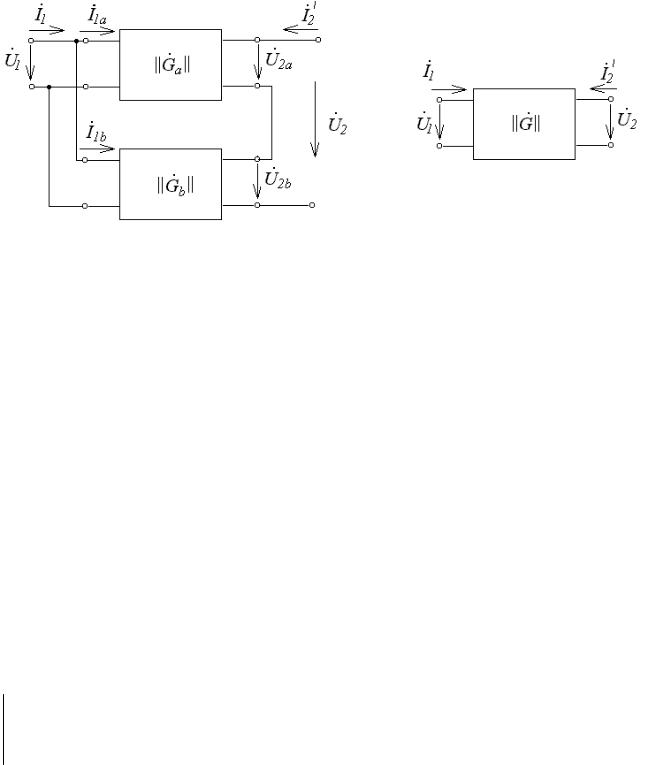
4.Параллельно-последовательное соединение четырехполюсников.
Врассматриваемой схеме (рис.94, а) входные зажимы составляющих четырехполюсников соединены параллельно, а выходные
−последовательно.
а |
б |
Рис.94
Уравнения четырехполюсников в данном случае удобно представить в системе G−параметров.
|
|
I& |
|
|
|
|
= |
|
|
|
G& G& |
|
|
|
|
|
|
U& |
|
|
|
|
= |
|
G& |
|
|
|
U& |
|
|
|
, |
|
|
|
I& |
|
|
|
|
= |
|
G& |
|
|
|
U& |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
11 12 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
|
|
U&2 |
|
|
|
|
|
|
|
|
G&21G&22 |
|
|
|
|
|
|
I&2′ |
|
|
|
|
|
|
a |
|
|
|
I&2′ |
|
|
|
|
|
|
|
U&2 |
|
|
|
b |
|
|
b |
|
|
|
I&2′ |
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Из схемы (рис.94, а) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
U&1 =U&1a =U&1b , |
U&2 =U&2a +U&2b , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
I&1 = I&1a + I&1b , I&2′ = I&2′a = I&2′b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Для эквивалентного четырехполюсника (рис.94, б) получим:
|
I& |
2 |
|
= |
|
G& |
|
|
|
U& |
|
|
|
, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
U& |
|
|
|
|
I&2′ |
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
