Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Метрология, стандартизация и сертификация

Файл:

Основы Теории Цепей

.pdf

Скачиваний:

Добавлен:

23.02.2023

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

101

Следует также отметить, что фазы Z&1BH и Z&2 BH равны соответственно и противоположны по знаку фазам Z&22 и Z&11

X1BH	= −	X22	,	X2 BH	= −	X11	.
R		R		R
						R
1BH		2		2 BH		1

Векторные диаграммы связанных контуров

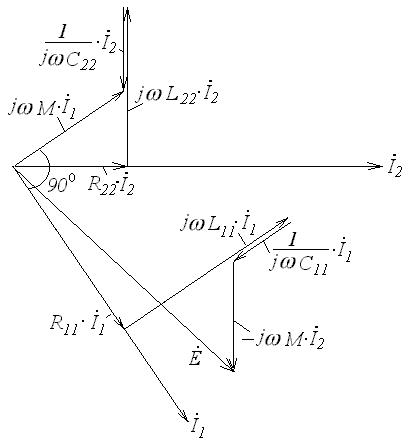
Векторные диаграммы токов и напряжений в связанных контурах рассмотрим на примере схемы с трансформаторной связью (рис.78, а). Схема замещения первого контура содержит кроме собственных элементов еще и вно-

симые активное R1BH и реактивное X1BH сопротивления (рис.78, б).

Для построения векторных диаграмм удобно воспользоваться системой уравнений связанных контуров:

E& = Z&11I&1 − Z&12 I&2 ,

0 = −Z&12 I&1 + Z&22 I&2.

С учетом вносимых сопротивлений эти уравнения можно представить в виде:

	&			1	&			&
E = (R11 + jωL11 +				jωC11	)I1	− jωMI2				,
				jωC11
							1
		&					1			&		&
	0 = − jωMI		+ (R	+ jωL +					)Z I .
		1	22		22		jωC22				22	2
		1	22		22						22	2

Здесь		R11 = R1 + R1BH и R22			= R2 + R2 BH .

102

Рис.78

Предположим, что контуры работают на частоте выше резонансной, т. е. их реактивное сопротивление имеет индуктивный характер. Тогда напряжения на индуктивностях по величине больше напряжений на емкостях.

Выбрав произвольно направление тока I&2 , откладываем напряжение на сопротивлении R22 , совпадающее по направлению с током I&2 (рис.79). Напряжение на индуктивности L22 опережает, а на емкости C22 отстает от тока

I&2	на	π	. Согласно второму уравнению сумма напряжений на элементах
		2
второго контура равна напряжению на сопротивлении связи jωMI& .
					π	1
		&	&		π	.
	Ток I		отстает от напряжения jωMI	на		.
		1		1	2
					2

Рис.79

103

Аналогично строим векторную диаграмму для первого контура.

Лекция 12.

Настройка связанных контуров

Под настройкой системы связанных контуров понимается подбор значений параметров контуров, включая и коэффициент связи между контурами, таким образом, чтобы обеспечить получение максимальной мощности или максимального к. п. д. передачи энергии, или нужной полосы пропускания при заданной частоте и ЭДС источника сигнала.

Для выяснения условий настройки необходимо исследовать зависимость тока второго контура от настройки каждого контура и величины коэффициента связи.

R + R

+ j( X

+ X

)

+ Z

1BH

Амплитуды токов в контурах

I1 =

(R +

X 2

R )

( X

−

X 2

)

Z22

X12

X 2

(R +

R )

( X

−

)

X 2

Z22

В зависимости от того, параметры какого контура изменяются при настройке, различают несколько способов настройки.

Первый частный резонанс. Ток во втором контуре имеет максимум, когда максимален ток в первом контуре, таким образом, настроив первый контур так, чтобы

X		−	X 2	X		= 0 ,
	11		12		22

			&2
			&2
			Z22

104

получим

I =

, I

2 max

X12

1max

X122

R1 +

Z22

Таким образом, для получения первого частного резонанса необходимо при неизменных параметрах второго контура и сопротивления связи изменять параметры первого контура.

Очевидно, что I2 max не является наибольшим при данных параметрах

контуров и ЭДС источника сигнала. Для достижения наибольшего значения тока во втором контуре необходимо подобрать еще оптимальную связь между контурами.

Первый сложный резонанс. При настроенном в резонанс первом контуре оптимальное сопротивление связи можно найти, приравняв к нулю первую

производную выражения для второго тока по X12 .

E(R

X122

R −

X122

R )

2 max

Z22

= 0

X12

(R +

X122

R )2

Z&2

Отсюда

X 2

Z22

−

R =

Z22

и оптимальное сопротивление связи

X12opt

Токи в контурах при этом сопротивлении связи

						105
I		=	E	, I		=	E	.
	2mm				1max ( X12 opt )
		2	R1R2				2R1

Второй частный резонанс. В этом случае при неизменных параметрах первого контура и неизменной связи настраивается второй контур так, чтобы

−

X 2

= 0 ,

тогда

X12

X 2

R )

+ ( X

−

)

X 2

I2 max =		E			X12	.

			X122		Z&

	R2 +			R1
	R2 +	&2		R1	11
			Z
			Z
			11

Второй сложный резонанс. Если после настройки на второй частный резонанс подобрать оптимальное сопротивление связи, то можно получить

2mm

1max ( X12 opt )

2 R1R2

2R2

Z&11

при

12opt

Полный резонанс. В этом случае каждый из контуров отдельно настраивается в резонанс на частоту генератора. Для этого при настройке одного контура другой размыкается. Практически вместо размыкания контуров доста-

106

точно ослабить связь между контурами настолько, чтобы вносимыми сопротивлениями из одного контура в другой можно было бы пренебречь. После раздельной настройки каждого контура подбирается оптимальная связь.

= X

= 0,

= R ,

= R .

2 max

X12

R +

X 2

R R +

X 2

2 max

E(R R + X 2 − 2X 2 )

= 0,

(R R + X 2

откуда

R R ,

2mm

, I

1max ( X12 opt )

12opt

1 2

R1R2

2R1

Значения токов в контурах в этом режиме не отличаются от полученных при настройке в сложный резонанс. Сопротивление связи, при котором ток во втором контуре достигает максимально возможного значения, получается

много меньше, чем при сложном резонансе и составляет единицы Ом. Коэффициент связи, при котором система настроена в полный резонанс,

называется оптимальным

opt

≈

X12

R1R2

= d d

ρ1ρ2

Q1Q2

где

Q =

− добротности контуров.

Так как добротность контуров, используемых в радиотехнике, имеет величину примерно 100−300, коэффициенты связи обычно составляют единицы или доли процентов.

Энергетические соотношения в двухконтурной системе

107

Рассматривая второй контур как нагрузочный, содержащий полезное сопротивление R2 , можно ввести понятие коэффициента полезного действия двухконтурной системы

η =

+ P

где P1 −мощность, расходуемая в сопротивлении R1 ,

P2 −мощность, расходуемая в сопротивлении

R2 ,

P1 + P2 −мощность, отдаваемая генератором.

P = R

I 2

P = R

I 2

= R

I 2

X 2

Z222

1 2

2 2

1BH 2

2 2

При настройке второго контура в резонанс

Z 2

= R ,

X 2

22 P

1BH

η =

X 2

1BH

+ P

+ R

R R

X 2

1BH

1 2

1 + R

1BH

Таким образом, для получения высокого η необходимо увеличивать

	R1BH	, т. е. снижать R и подбирать достаточно сильную связь (это применя-

1
	R1
ется на выходе передатчиков, когда вторым контуром является антенна с
η=0,8-0,9).				R1R2
	При полном резонансе X12 =		R1R2 и η =			= 0,5,
				R1R2	+ R1R2

т. е. для получения максимального коэффициента полезного действия полный и сложный резонансы не пригодны.

Если поставить задачу передачи максимальной мощности во второй кон-

тур при заданных	E& и R	то, очевидно, P	будет при условии согласо-
	1	2 max

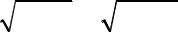
108

вания R1 = R1BH , т. е. при η=0,5. Для получения P2 max необходимо использовать полный и сложный резонансы.

Лекция 13.

Резонансные кривые связанных контуров

Основной интерес представляет поведение амплитуд токов в контурах вблизи резонансных частот системы. Для простоты полагаем, что резонансные частоты контуров равны между собой:

=ω

L11C11

L22C22

Полные сопротивления контуров

= R + jX

= R (1 + j

X11

= R + jX

= R (1 + j

X22

) .

На частотах близких к резонансной частоте

∆ω <<1,

=ξ = Q(

− ω0 ) ≈

2(ω −ω0 )

Q и

ω0

= R + jX

≈ R (1 + jξ ) ,

= R + jX

≈ R (1 + jξ

) ,

где ξ1, ξ2 −обобщенная расстройка первого и второго контуров.

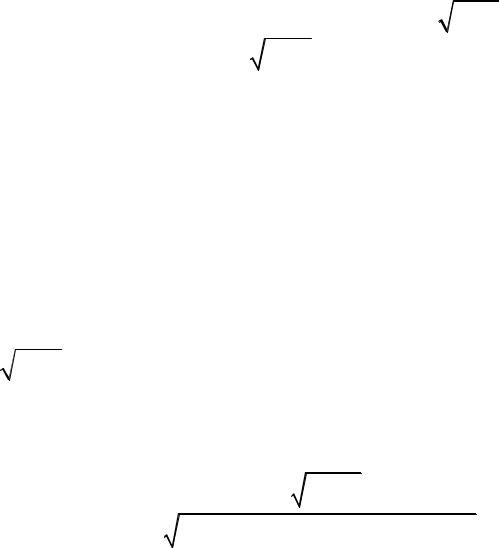
Ток в первом контуре

109

X122

(1 + jξ ) +

X122

(1 + jξ

)

R (1 + jξ )

X 2

1 1 −ξξ

+ j(ξ

+ξ

)

R1R2

Ток во втором контуре

± j

X12

I&2 =

± jX

R1R2

X12

Z22

R1R2 1

−ξξ

X12

+ j(ξ

+ξ

)

1 2

R R

На частотах, близких к резонансной частоте

X 2

ρ ρ

= k2Q Q .

R1R2

ρ1ρ2 R1R2

Кроме того, выше было получено

= 2I

2mm

1max ( X12 opt )

R1R2

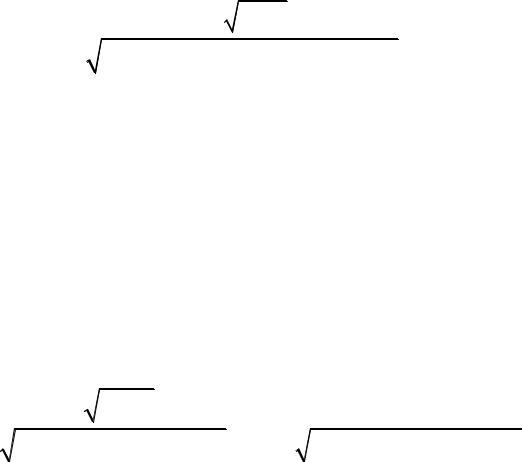
Таким образом, подставив последние выражения в формулы для токов, получим уравнения нормированных резонансных кривых первого и второго контуров

n1 =	I&	=			2 1 +ξ22							e	− j(ϕ −ϕ		)	,
&	1												12	2
	I1max ( X12 opt )	(1	−ξ ξ	2	+ k	2Q Q )2		+ (ξ	+ξ	2	)2
			1	2		1	2	1		2

110

I&2

2k Q1Q2

− j(ϕ12

±π2 )

I2mm

(1 −ξ ξ

+ k

2Q Q )2

+ (ξ

+ξ

где

ξ1 +ξ2

ϕ12

= arctg

, ϕ2 = arctgξ2 ,

−фаза X12 ,

−ξ ξ

+ k

2Q Q

+π2 −соответствует емкостной связи, − π2 −магнитной связи.

Для одинаковых контуров, использующихся в полосовых фильтрах при-

емников,

Q1 = Q2 = Q, ξ1 =ξ2 =ξ ,

n1 =

2 1 +ξ2

, n2 =

2kQ

−

(1 −

(1 −ξ2 + k2Q2 )2 + 4ξ2

2 + k2Q2 )2 + 4ξ2

−амплитудно-частотные характеристики первого и второго контуров,

ϕ = arctg

2ξ

− arctgξ , ϕ

= arctg

2ξ

± π −

−ξ2 + k2Q2

−фазочастотные характеристики первого и второго контуров.

На рис.80 приведены АЧХ и ФЧХ второго контура в функции обобщенной расстройки при пяти различных значениях произведения kQ. (kQ характеризует степень связи контуров и называется параметром или фактором связи).

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете Метрология, стандартизация и сертификация

#
23.02.2023361.47 Кб6История создания систем качества на отечественных предприятиях Кулакова О.Г.doc
#
23.02.2023361.47 Кб2История создания систем качества.doc
#
23.02.202357.38 Кб1Классы чистоты Большая советская энциклопедия (БСЭ)..mht
#
23.02.2023997.02 Кб8Метрология.pdf
#
23.02.2023728.67 Кб8Обработка Результатов Измерений.pdf
#
23.02.20231.23 Mб10Основы Теории Цепей.pdf
#
23.02.20234.18 Mб2Теория Измерений.mht
#
23.02.20232.03 Mб9Цифровые Измерительные Устройства.pdf