
Основы Теории Цепей
.pdf
91
ω0 L1 |
|
ω0 L2 |
|
1 |
|
R1 << X1 и R2 << X2 ). |
|
= − |
− |
(при |
|||||
|
|||||||
|
|
|
|
ω0C |
|
||
ω |
|
(L |
+ L )− |
1 |
= 0 |
или ω |
|
= |
1 |
( f |
|
= |
ω0 |
), |
|
|
ω0C |
0 |
LC |
0 |
|||||||||||
|
0 |
|
1 |
2 |
|
|
|
|
|
2π |
|
||||
где |
L = L1 + L2 . |
|
|
|
|
|
|
|
|
|
|
||||
Обозначим p = LL1 − коэффициент включения, тогда
X1 =ω0 L1 = pω0 L, ω0 L = ρ .
Входное сопротивление контура при резонансе
Z |
BX P |
= R |
= |
X12 P |
= |
p2 ρ2 |
= p2 R |
(R = R + R ). |
|
|
|||||||
|
э |
R |
R |
эmax |
1 2 |
|||
|
|
|
|
|
|
|||
Кроме резонанса токов, в контуре II вида возможен и резонанс напряжений в ветви L2C ;
X |
|
=ω |
L − |
1 |
= 0, ω |
|
= |
1 |
>ω |
|
( f |
|
= |
ω02 |
). |
|
ω02C |
|
L2C |
|
02 |
||||||||||
|
2 |
|
02 2 |
|
02 |
|
|
0 |
|
|
2π |
|
При частоте ω =ω02 сопротивление второй ветви резко падает до величины R2 .
Поскольку L2 = L − L1 = L(1 − p), то
ω02 |
= |
|
1 |
= |
ω0 |
, |
||
L(1 |
− p)C |
1 |
− p |
|||||
|
|
|
|
|||||
т.е. чем меньше коэффициент включения, тем ближе ω02 к ω0 . Модуль входного сопротивления контура при небольших расстройках
|
|
|
|
|
92 |
|
ZBX |
|
= p |
2 |
Rэmax |
|
. |
|
|
|||||
|
|
1 +ξ |
2 |
|||
|
|
|
|
|
||
Если контур питается от идеального источника тока, то напряжение на нем изменяется с частотой также как и ZBX .
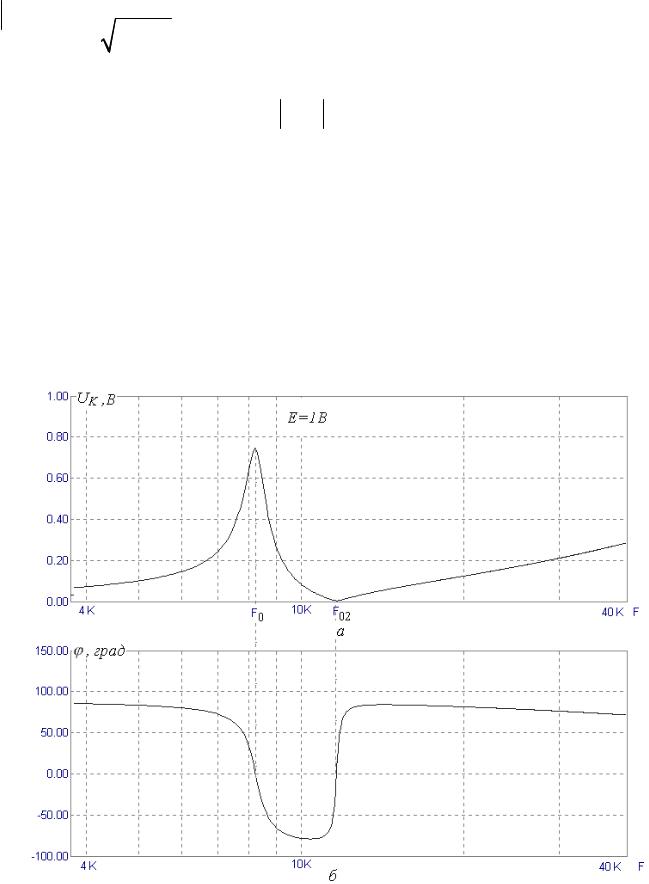
На рис.74, а приведена зависимость напряжения от частоты на реальном контуре с параметрами L1 = L2 = 25мГн, C = 7,5нФ, R = 40Oм
при подключении его к источнику Е =1В с внутренним сопротивлением
Ri =10кОм.
Контур II вида не только выделяет сигналы с частотой, близкой к ω0 , но и более сильно, чем контур I вида, подавляет сигналы, близкие по частоте к
ω02 .
На рис.74, б представлена ФЧХ, соответствующая данной амплитудночастотной характеристике.
Рис.74

93
Действительно, на частотах 0 <ω <ω0 входное сопротивление кон-
тура имеет индуктивный характер, поскольку на частоте ниже резонансной в параллельном контуре сопротивление левой ветви (рис.73, а) меньше сопротивления правой ветви, имеющей ёмкостной характер. На частотах
ω0 <ω <ω02 входное сопротивление определяется ёмкостным сопротивлением правой ветви, поскольку последовательный контур L2C на
ω <ω02 имеет входное сопротивление ёмкостного характера. На частотах ω >ω0 сопротивления ветвей X1 и X2 имеют индуктивный характер и ФЧХ стремится к 90o при ω → ∞. Следует отметить, что в колебательном контуре с потерями ФЧХ нигде не достигает значения ±90o.
В контуре III вида (рис.73, б) X1 = −X2 при
|
ω0 L − |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
= − |
|
|
|
, ( R1 << X1 и R2 << X2 ). |
||||||||||||||
|
ω0C1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
ω0C2 |
|
|
|
|
|
|
|||||||||
|
Откуда |
ω0 = |
|
1 |
|
|
, |
где |
C = |
|
|
C1C2 |
. |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
LC |
|
|
|
|
C1 +C2 |
|||||||
|
Обозначив |
C |
= p − коэффициент |
включения, |
|||||||||||||||||
|
|
||||||||||||||||||||
получим |
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
R = |
|
1 |
|
|
= |
|
|
1 |
|
|
|
= p2 |
|
ρ2 |
= p2Q ρ. |
||||||
R(ω0C2 )2 |
|
|
|
|
C 2 |
|
|
|
|||||||||||||
э |
|
|
|
|
|
|
|
|
|
|
R |
|
|
||||||||
|
|
|
|
|
|
|
|
|
R |
ω0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|||
Как и в контуре II вида, в контуре III вида возможен резонанс напряжений в первой ветви, когда X1 = 0
94
|
ω01L − |
1 |
|
= 0 , ω01 = |
1 |
<ω0 ( f01 = |
ω01 ). |
|
|
|
|||||||
ω01C1 |
|
|||||||
|
|
|
|
LC1 |
2π |
|||
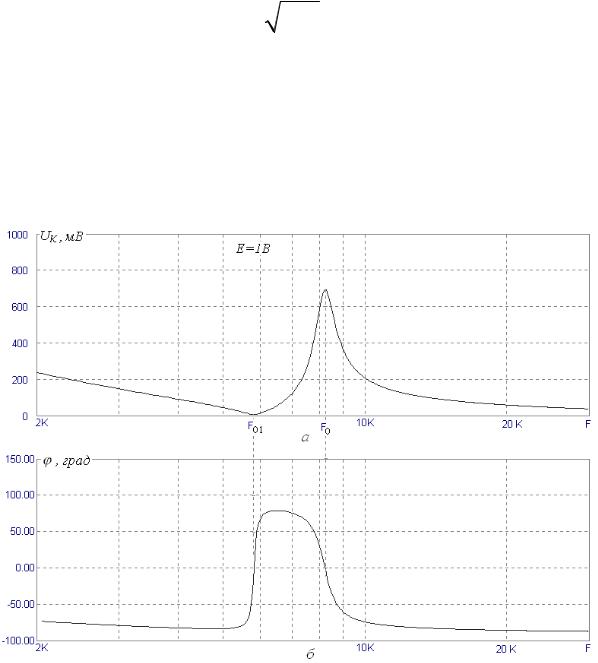
АЧХ и ФЧХ для контура с параметрами L = 50мГн, |
|
|||||||
C1 = C2 =15нФ, |
R = 40Oм при подключении его к источнику |
|||||||
Е =1В с внутренним сопротивлением Ri =10кОм представлены на рис.75.
Рис.75
Следует отметить, что для передачи максимальной мощности от генератора к контуру следует выбрать коэффициент включения

95
p |
= |
Ri R |
= |
Ri |
R |
= R |
= p2 |
ρ2 |
. |
||
|
|
|
|||||||||
OPT |
|
ρ |
2 |
|
Rэmax |
|
i |
э |
OPT |
R |
|
|
|
|
|
|
|
|
|
|
|||
Лекция 11.
Колебательные системы. Связанные контуры
Рассмотренные ранее одиночные колебательные контуры обладают недостаточно высокой избирательностью ввиду невысокой крутизны скатов резонансной кривой, что препятствует четкому разделению сигналов по частоте. Для повышения избирательности применяют сложные колебательные системы из нескольких контуров связанных между собой различным способом.
Чаще всего применяют системы из двух связанных контуров.
Виды связи
В зависимости от того, как осуществляется связь между контурами через общий магнитный поток или общее электрическое поле различают
магнитную (индуктивную) (рис.76, а, б) или электрическую (рис.76, в, г)
связь. Применяют также и комбинированную индуктивно-ёмкостную связь
(рис.77, а).
Кроме того связь подразделяют на внешнюю, когда элементы связи не входят в состав контуров и внутреннюю, когда элементы связи являются общими для двух контуров.
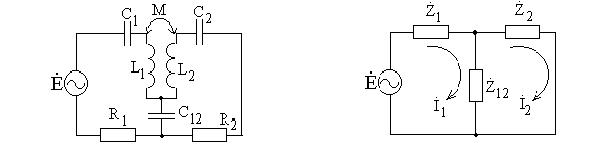
|
|
а) трансформаторная |
б) автотрансформаторная |
(внешняя магнитная) |
(внутренняя магнитная) |
|
|
|
|
96
в) внутренняя ёмкостная |
г) внешняя ёмкостная |
Рис.76
При рассмотрении стационарного режима любую из двухконтурных цепей можно представить в виде обобщенной схемы (рис.77, б).
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
б |
|
|
|
|
|
Рис.77 |
|
|
|
|
|
|
|
|
|
|
|
|
В общем случае Z& |
и |
Z& |
имеют L , |
C , |
R и |
L , C |
2 |
, R , входящие |
||||
1 |
|
2 |
1 |
1 |
1 |
2 |
|
|
2 |
|
|
|
только в первый или во второй контуры, |
Z& |
имеет |
L , |
C , |
R |
− общие |
||||||
для двух контуров. |
|
|
|
12 |
|
12 |
|
|
12 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результирующие величины L, C, R , получаемые при обходе данного |
||||||||||||
контура при разомкнутом втором: L11, C11, |
R11 и |
L22 , |
C22 , |
R22 . |
||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
Z& |
= R + jωL + |
|
1 |
, |
|
|||
|
jωC |
|||||||
11 |
11 |
11 |
|
|
|
|
||
|
|
|
|
11 |
|
|
|
|
Z& |
= R + jωL + |
|
1 |
|
. |
|||
|
|
|||||||
22 |
22 |
22 |
|
|
jωC22 |
|||
|
Общее сопротивление |
|
|
|
||||
Z& |
= R + jωL + |
1 |
. |
|||||
|
||||||||
12 |
12 |
12 |
|
|
jωC |
|
|
|
|
|
|
|
12 |
|
|
|
|
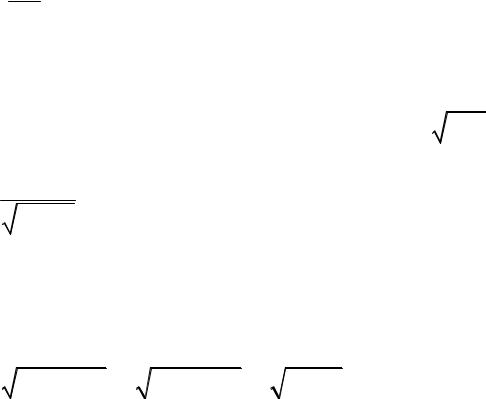
97
Очевидно, что
Z&11 = Z&1 + Z&12 , Z&22 = Z&2 + Z&12 .
Коэффициент связи
Для количественной оценки взаимного влияния контуров применяется понятие коэффициента связи. Рассмотрим, например, случай трансформаторной связи (рис.76, а). Пусть при разомкнутом втором контуре в первом про-
текает ток I&1 . Тогда отношение э. д. с., индуктированной в катушке L22 , к полному напряжению на индуктивности L11
k |
= |
|
E& |
= |
jωMI& |
= |
M |
|
|
|
|
2 |
1 |
|
, |
||||
& |
|
& |
|
||||||
1 |
|
|
|
|
L |
|
|||
|
|
U |
L |
|
jωL I |
|
|
||
|
|
|
|
|
11 1 |
|
11 |
|
|
|
|
|
|
11 |
|
|
|
|
|
где k1 имеет смысл коэффициента трансформации и является величиной, ха-
рактеризующей степень связи первого контура со вторым.
Если генератор включить со стороны второго контура, а первый контур разомкнуть, то
k2 = M .
L22
При одновременном протекании токов в обоих контурах имеется взаимное влияние между ними тем большее, чем больше произведение k1k2 .
Коэффициент связи между контурами определяют k = k1k2 . Для трансформаторной связи
k = M .
L11L22
В общем случае коэффициент связи k определяется как отношение сопротивления связи к среднему геометрическому сопротивлений того же рода обоих контуров. Для рассмотренной выше трансформаторной связи
k = |
X12 |
|
= |
ωM |
|
= |
M |
|
. |
ωL ωL |
ωL ωL |
L L |
|||||||
|
11 |
22 |
|
11 |
22 |
|
11 |
22 |
|
98
Для автотрансформаторной связи (рис.76, б)
k = |
|
|
|
|
|
|
X12 |
|
|
= |
|
|
|
|
ωL12 |
|
|
|
|
= |
|
|
L12 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L L |
||||||||||||
|
|
|
|
|
ωL ωL |
|
|
ωL |
ωL |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
11 |
|
|
22 |
|
|
|
|
|
|
|
|
|
11 |
|
|
22 |
|
|
|
|
|
11 |
22 |
|
|
||||||
Для внутренней ёмкостной связи (рис.76, в) |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
C11C22 |
|
|
|||||||
k = |
|
|
|
|
|
ωC |
|
|
|
|
|
= |
|
|
|
|
|
C |
|
|
|
|
= |
|
|
|
|
|||||||||||
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
, |
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
C12 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ωC11 |
|
ωC22 |
|
|
|
|
|
|
|
C11 |
|
C22 |
|
|
|
|
|
|
|
|||||||||||||
где C |
|
|
= |
C1C12 |
, |
C |
22 |
= |
|
|
C2C12 |
. |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
11 |
|
|
C1 |
+C12 |
|
|
|
|
|
|
|
|
C2 |
+C12 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
При изменении ёмкости |
C12 |
от 0 до ∞ коэффициент связи изменяется |
|||||||||||||||||||||||||||||||||||
от k = 1 до |
k = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
При |
|
|
C12 = 0 система вырождается в один контур, при C12 → ∞ |
||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
→ 0 и контуры оказываются не связанными. |
||||||||||||||||||||||||||||||||
ωC |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если связь между контурами осуществляется через чисто реактивное сопротивление и контуры настроены на одну частоту, совпадающую с частотой генератора, то индуктивное и ёмкостное сопротивления каждого контура приблизительно равны характеристическому сопротивлению и коэффициент связи может быть определен по формуле
k = |
|
|
X12 |
|
|
, |
|
|
|||||
|
|
ρ ρ |
2 |
|||
|
|
|
|
|||
|
|
1 |
|
|
||
где ρ1 и ρ2 − характеристические (волновые) сопротивления первого и второго контуров.
Соотношения между токами в связанных контурах
Для обобщенной схемы связанных контуров (рис.77, б) можно составить систему уравнений методом контурных токов

99
E& = Z&11I&1 − Z&12 I&2 ,
= −Z& I& + Z& I&
0 12 1 22 2.
Решив систему относительно токов в контурах, получим
I& |
= |
Z& |
I& |
, |
I& |
= |
|
|
|
|
|
E& |
|
|
, |
I& |
|
= |
|
|
|
|
E& |
|
|
|
|
Z& |
|
||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
, |
|||||||||||||||
& |
|
|
|
|
|
|
&2 |
|
|
|
|
|
|
|
|
& |
2 |
|
& |
||||||||||||||||||||
2 |
|
1 |
|
1 |
|
|
|
Z& |
− |
|
|
|
2 |
|
|
Z& |
− |
|
|
|
|||||||||||||||||||
|
|
Z22 |
|
|
|
|
|
|
|
|
|
Z |
12 |
|
|
|
|
|
|
|
Z |
12 |
|
|
Z22 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
& |
|
|
|
|
|
|
|
|
|
11 |
|
|
& |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z22 |
|
|
|
|
|
|
|
|
|
|
|
|
Z22 |
|
|
|
|
|||||
|
|
|
E& |
|
|
|
|
|
Z& |
|
|
|
|
|
Z& |
22 |
|
|
|
|
|
|
|
E& |
|
|
|
|
|
|
Z& |
|
|
|
|
|
|
||
I&2 = |
|
& |
2 |
|
|
|
|
|
Z& |
|
|
= |
|
|
|
&2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
& |
|
|
|
& |
11 |
|
|
|
|
|
|
|
& . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|||||||
|
|
Z& |
− |
Z |
12 |
|
|
|
Z |
22 |
|
|
|
Z |
22 |
|
|
|
|
|
Z& |
|
− |
Z |
12 |
|
|
|
Z |
11 |
|
|
|
|
|
||||
|
|
11 |
|
& |
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
22 |
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Z |
22 |
|
|
|
|
|
|
|
|
|
Z |
11 |
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|||||
Из выражения для тока в первом контуре следует, что влияние второго контура на первый можно оценить с помощью некоторого «вносимого» со-
противления, добавляемого к собственному сопротивлению Z&11,
|
|
&2 |
|
|
|
|
|
& |
|
||
т.е. |
Z& |
= − |
Z |
12 |
, |
тогда |
I& |
= |
|
E |
. |
|
|
& |
& |
||||||||
|
1BH |
& |
|
|
|
1 |
|
|
|||
|
|
|
Z |
22 |
|
|
|
|
Z |
+ Z |
|
|
|
|
|
|
|
|
|
11 |
1BH |
|
|
Таким же образом влияние первого контура на второй можно оценить с помощью вносимого сопротивления
Z&2 BH = − ZZ&&122 .
11
Чаще всего сопротивление связи чисто реактивное
Z& |
|
= ± jX |
|
|
Z&2 |
= −X 2 |
и Z& |
= |
X 2 |
|||
|
12 |
, тогда |
12 |
. |
||||||||
|
& |
|||||||||||
12 |
|
|
|
|
12 |
12 |
1BH |
|
|
|||
|
|
|
Z& |
= R + jX |
|
|
|
|
Z22 |
|||
|
При |
22 |
|
|
|
|
|
|||||
|
|
|
22 |
|
2 |
|
|
|
|
|
|
|
100
Z& |
= |
|
X 2 |
|
= |
|
X 2 |
|
R − j |
X 2 |
|
|
X |
|
|
||
|
12 |
|
|
12 |
|
|
12 |
|
|
|
, |
||||||
R |
+ jX |
|
R2 |
|
|
R2 |
+ X |
|
|
||||||||
1BH |
|
22 |
|
+ X 2 2 |
|
2 |
|
22 |
|
||||||||
|
|
2 |
|
|
2 |
|
22 |
|
|
2 |
|
|
22 |
|
|
|
|
|
|
|
|
|
|
Z& |
= R |
+ jX |
1BH |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
1BH |
|
1BH |
|
|
|
|
|
|
|
|
Аналогично, из первого контура во второй вносится сопротивление
Z& |
|
= |
X 2 |
= |
|
|
|
|
X 2 |
|
= R |
|
+ jX |
|
|
|
|
||||||
|
|
12 |
|
|
|
|
|
12 |
|
|
2 BH |
, |
|||||||||||
|
|
& |
|
|
|
|
|
|
|
||||||||||||||
2 BH |
|
|
|
|
|
R |
+ jX |
|
|
2 BH |
|
|
|
|
|
|
|||||||
|
|
|
Z |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
11 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
= |
|
X |
2 |
|
R , X |
|
|
= − j |
|
X |
2 |
|
X |
|
|
|
||||
где |
|
|
|
12 |
|
2 BH |
|
|
12 |
|
11 |
. |
|
||||||||||
|
|
& |
|
|
|
& |
|
|
|
||||||||||||||
|
|
2 BH |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|||
Следует отметить, что независимо от вида связи и настройки контуров действительная часть вносимого сопротивления всегда положительна. Это следует из физического эффекта поглощения энергии, поступающей из первого контура во второй.
Реактивная составляющая вносимого сопротивления может быть как положительной, так и отрицательной в зависимости от настройки контуров;
X |
|
=ωL |
− |
1 |
, |
|
ωC22 |
||||
|
22 |
22 |
|
|
|
приω >ω02 |
X22 > 0 и X1BH < 0, приω <ω02 X22 < 0 , X1BH > 0 |
||||
(ω02 − резонансная частота второго контура).
Это значит, что при индуктивной расстройке второго контура в первый вносится ёмкостное сопротивление, а при ёмкостной наоборот− индуктивное.
При резонансе второго контура
ω =ω |
|
X |
|
= 0, X |
|
= 0, а R |
= |
X 2 |
|
02 |
22 |
1BH |
12 |
, |
|||||
|
|||||||||
|
|
|
1BH |
|
R2 |
||||
|
|
|
|
|
|
|
|
||
т. е. чем меньше сопротивление потерь второго контура, тем больше вносимое сопротивление и большее влияние оказывает второй контур на режим работы первого контура.
