
Свойства операций над событиями
 ,
, - коммутативность,
- коммутативность, - ассоциативность
- ассоциативность - дистрибутивность
- дистрибутивность и
и ,
, ,
,
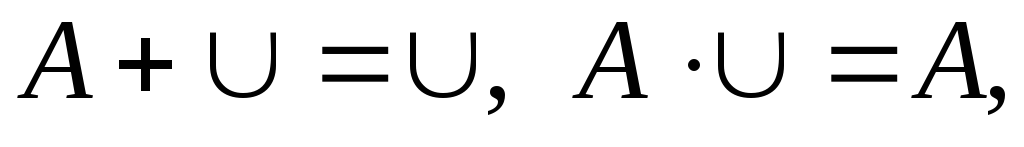 где
где - достоверное событие,
- достоверное событие, - невозможное событие.
- невозможное событие.
Теорема 1: Если события А и В несовместны, то вероятность их суммы равна сумме их вероятностей
![]() .
.
Доказательство:
Пусть n – общее число возможных элементарных исходов,
m1 – число исходов, благоприятствующих A,
m2 – число исходов, благоприятствующих B.
Число исходов благоприятствующих наступлению либо события А, события В равно m1+ m2 ,
значит ![]() .
.
Ч.т.д.
Следствие: Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
![]() .
.
Пример: В урне 8 белых, 5 синих и 2 красных шара. Какова вероятность того, что вынутый шар будет синего или красного цвета?
Решение: А – вынут синий шар,
В – вынут красный шар.
![]()
![]() .
.
Полная группа событий
Полной группой называется совокупность единственно возможных событий испытания.
Пример: Стрелок проводит по мишени 2 выстрела.
Полная группа
событий: ![]() - одно попадание,
- одно попадание,
![]() - два попадания,
- два попадания,
![]() -промах.
-промах.
Теорема 2:
Сумма вероятностей
![]() ,
образующих полную группу, равна единице:
,
образующих полную группу, равна единице:![]() .
.
Доказательство:
Т.к. появление одного из событий полной группы достоверно, а вероятность достоверного события равна 1, то
![]() или
или
Т.к. любые два события полной группы несовместны, то
![]() .
.
Теорема 3:
![]()
Доказательство:
Т.к.
![]() не совместные события, то
не совместные события, то
![]() ,
,
Но
![]() - это достоверное событие, т.е.
- это достоверное событие, т.е.![]() ,
значит,
,
значит,
![]() ЧТД.
ЧТД.
Пример: Один лотерейный билет выигрывает с вероятностью 0,0001. Какова вероятность того, что владелец одного билета ничего не выиграет?
![]() .
.
Теорема 4:
Вероятность
совместного появления двух независимых
событий равна произведению вероятностей
этих событий:
![]() .
(без доказательства).
.
(без доказательства).
Пример: Найти вероятность появления герба при одном бросании двух монет.
![]() .
.
Определение: Событие A называется зависимым от события B, если вероятность события A меняется в зависимости от того, произошло событие B или нет.
Пример: Пусть в урне 5 шаров: 2 белых и 3 черных. Два человека извлекают из урны по одному шару. A – появление белого шара у первого человека, B – появление белого шара у второго человека.
![]() ,
но
,
но
![]() ,
в зависимости, что вытащил первый человек
– белый или черный шар.
,
в зависимости, что вытащил первый человек
– белый или черный шар.
Определение:
Условной вероятностью
![]() называется вероятность событияA
, вычисленную
при условии, что событие B
произошло.
называется вероятность событияA
, вычисленную
при условии, что событие B
произошло.
Теорема 5:
![]() .
.
Доказательство:
Пусть испытание, в котором могут появиться события A и B имеется n.
m(B) – число исходов, благоприятных B,
m(AB) – число исходов, благоприятных AB.
![]() ,
,
В знаменателе стоит m(B), т.к. из определения условной вероятности, мы должны учитывать только те исходы, в которых произошло событие B.
![]() .
ЧТД
.
ЧТД
Следствие:
![]() ,
,![]() .
.
Эти формулы можно распространить на любое число событий:
![]()
Пример: Из колоды карт выбирают две карты. Какова вероятность, что будут вынуты 2 туза?
Решение: I
способ.
![]() .
.
II
способ.
 .
.
Определение: События A и B называются независимыми, если вероятность каждого из них не зависит от того, произошло другое событие или нет, т.е.
![]() ,
т.е.
,
т.е.
![]() (теорема
4).
(теорема
4).
Теорема 6: Вероятность двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
![]() .
.
Доказательство:
n – общее число исходов,
m – число исходов, благоприятных A,
k – число исходов, благоприятных B,
l – число исходов благоприятных и A и B.
![]() .
.
В сумме m+k дважды учтены исходы, благоприятные AB, поэтому число случаев, благоприятных событию A+B будет m + k – l, значит,
![]() .
.
Пример: Два стрелка независимо один от другого делают по одному выстрелу по одной и той же мишени. Вероятность поражения мишени первым стрелком – 0,5, вторым - 0,6. Какова вероятность того, что мишень будет поражена?
Решение:
I способ. С – мишень поражена,
А – мишень поразил первый стрелок,
B- мишень поразил второй стрелок.
![]()
II способ.
![]() .
.
III способ.
![]() .
.
