
даишев лекция по дифурам
.pdf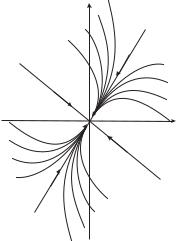
I. |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A. Корни λ1 |
и λ2 |
характеристического уравнения веще- |
|||||||||||||
ственны и различны. Тогда |
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
= c1e |
λ1t |
|
α1 |
|
+ c2e |
λ2t |
|
β1 |
|
, |
(15.4) |
|
|
y |
|
|
|
α |
|
|
|
β |
2 |
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть, иначе говоря,
x(t) = c1α1eλ1t + c2β1eλ2t , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ1t |
+ c2β2e |
λ2t |
. |
y(t) = c1α2e |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1. λ1 < 0, λ2 < 0; пусть |
λ1 = −p 2, λ2 = −q2 |
|||
случае решение (15.5) примет вид
x(t) = C1α1e−p2t + C2β1e−q2t , |
||||
|
2 |
t |
2 |
t |
|
p |
q |
||
|
|
|
|
|
y(t) = C1α2e− |
|
|
+ C2β2e− . |
|
|
|
|
|
|
|
|
|
|
|
(15.5)
. В этом
(15.6)
|
|
x |
Точка покоя x = 0, y = 0 |
устойчива |
|||||
|
|
|
|
|
|
|
|
||
|
|
|
и асимптотически устойчива, так как из-за |
||||||
|
|
|
наличия множителей |
e−p 2t и |
e−q2t |
все |
|||
|
|
|
точки, находящиеся в момент времени |
t0 в |
|||||
Рис. 10. |
|
|
δ -окрестности начала координат, при доста- |
||||||
|
|
точно большом t переходят в точки, лежа- |
|||||||
Устойчивый узел |
|
|
|||||||
щие в сколь угодно малой |
ε -окрестности начала координат, а |
||||||||
при t → ∞ и |
x → 0, и |
y → 0. |
|
|
|
|
|||
Если в (15.6) положить C1 = 0 или |
C2 = 0, получим два |
||||||||
выделенных решения. Эти решения имеют вид |
|
|
|||||||
x(t) = α1C1e−p2t , |
или |
x(t) = C2β1e−q2t , |
|
|
|||||
|
|
2 |
t |
|
2 |
t |
|
|
|
|
|
p |
|
|
q |
|
|
||
|
|
|
|
|
|
|
|
|
|
y(t) = α2C1e− |
|
|
|
y(t) = C2β2e− . |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
111

В плоскости (x, |
y) — это прямая |
x |
= |
|
α1 |
в случае первого |
|||||
|
|
α |
|||||||||
|
|
|
|
|
|
y |
|
|
|||
|
|
x |
|
β1 |
|
|
|
2 |
|
||
решения или прямая |
= |
в случае второго. Оба эти решения |
|||||||||
y |
|
||||||||||
устойчивы, и при |
|
β |
и x → 0, |
и |
y → 0 вдоль этих |
||||||
t → ∞, 2 |
|||||||||||
прямых.
Покажем, что кривые входят в особую точку, касаясь той прямой, которая направлена вдоль собственного вектора, соответствующего меньшему по абсолютной величине значению λ. Пусть p2 < q2. Запишем (15.6) в виде
x(t) = e−p2t C1α1 + C2β1e−(q2−p2)t , |
||||||
|
2 |
t |
(q |
2 |
2 |
(15.7) |
|
p |
|
p |
)t |
||
|
|
|
C1α2 + C2β2e− − |
|
. |
|
y(t) = e− |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Легко видеть, что поскольку q2 − p2 > 0, то при t → +∞ вторые слагаемые в скобках быстро убывают, поэтому при боль-
ших значениях t |
поведение решения определяется только пер- |
|||||
|
x(t) |
≈ |
e−p2tC1α1, |
|
||
|
|
|
p t |
|
|
|
выми слагаемыми |
|
|
|
|
то есть интегральные |
|
|
|
2 |
|
|||
|
y(t) ≈ e− |
|
C1α2, |
α2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривые асимптотически стремятся к прямой y = α1 x.
Однако же "бесконечно давно", то есть при t → −∞, именно вторые слагаемые в (15.6) превалируют над первыми, и общее направление движения точек определяется, главным образом,
прямой y = β2 x. β1
На рисунке 10 схематично изображено расположение траекторий около точки покоя рассматриваемого типа, называемой устойчивым узлом. Стрелками показано направление движе-
ния по траектории при возрастании |
t. |
A2. λ1 > 0, λ2 > 0. Пусть |
λ1 = p 2, λ2 = q2 . При |
112
замене t → − t, мы имеем ситуацию A1. Траектории имеют тот же вид, только точка по траектории движется от начала координат и при больших значениях t точки, которые в момент времени t0 находились вблизи начала координат, удаляются из ε-окрестности начала координат. Это — неустойчивый узел.
A3. λ1 > 0, λ2 < 0; |
пусть |
λ1 = p 2, |
Точка покоя неустойчива, так как |
||
взяв решение x(t) = = C1α1ep2t, |
y(t) = |
|
C1α2ep2t (т.е. положив C2 |
= 0 ), полу- |
|
чим, что точка по прямой |
|
α |
y = |
α12 x |
|
удаляется от начала координат, при t > t0 она покидает ε-окрестность начала координат (x, y) = (0, 0).
λ2 = −q2 .
y 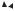
x
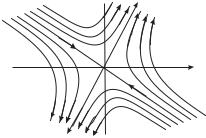
Рис. 11. Седло.
Вместе с тем существует другая прямая (при |
C1 |
= |
0) |
|
x(t) = C2β1e−q2t, y(t) = C2β2e−q2t, то есть y = β2 |
x, |
где точки |
||
(x, y) → (0, 0). Если же и C1 |
= 0, и C2 |
β1 |
|
|
= 0, |
то как при |
|||
t → +∞, так и при t → −∞, |
точка покидает начало коорди- |
|||
нат. Точка покоя рассматриваемого типа называется седлом, а
прямые y = |
α2 |
x |
и y = |
β2 |
x, вдоль которых точка или убега- |
|
α1 |
|
|
β |
|
|
|
|
|
1 |
|
ет от начала координат, или приближается к нему, называются
сепаратриссами седла. Качественное поведение интегральных кривых в окрестности точки покоя изображено на рисунке 11.
B. Корни λ1 и λ2 |
характеристического уравнения ком- |
плексные: λ1 = α + iβ, |
λ2 = α − iβ. Решение системы в этом |
случае может быть записано в виде
113
x(t) = eαt(C1 cos βt + C2 sin βt) , |
|
||
|
|
|
|
|
αt |
|
|
|
где C1 |
и C2 — произвольные |
|
|
|
||
y(t) = e |
|
(C3 cos βt + C4 sin βt) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянные, а C3 |
и C4 |
— линейные комбинации постоянных |
|
C1 и C2. |
|
|
|
B1. α = 0, |
β = 0. |
В этом случае решение исследуемой |
|
системы уравнений имеет вид |
x(t) = C1 cos βt + C2 sin βt , |
||
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
y(t) = C cos βt + C sin βt .
3 4
Поскольку и sin βt и cos βt — периодические функции с одним и тем же периодом 2π/β, зна-
 чения x(t) и y(t) через период повторятся, а
чения x(t) и y(t) через период повторятся, а
x
это означает, что через этот промежуток времени точка вернётся в исходное положение, т. е. траектория замкнётся. Следовательно, в этом случае
мы имеем замкнутые циклы, окружающие точку (x, y) = (0, 0). Решение устойчиво. Такая точка покоя называется центром. Качественное поведение интегральных кривых в окрестности этой точки покоя изображено на рисунке 12.
B2. α < 0, пусть α = −p 2, β = 0.
Наличие множителя e−p 2t в решении означает, что точка по спирали стремится к началу координат при t → ∞. Решение устойчиво, более того, решение асимптотически устойчиво. Такая точка покоя называется устойчивым фокусом. Качественное поведение интегральных кривых в окрестности фокуса показано на рисунке 13.
B3. α > 0. Пусть α = p 2, β = 0. Этот случай при
114
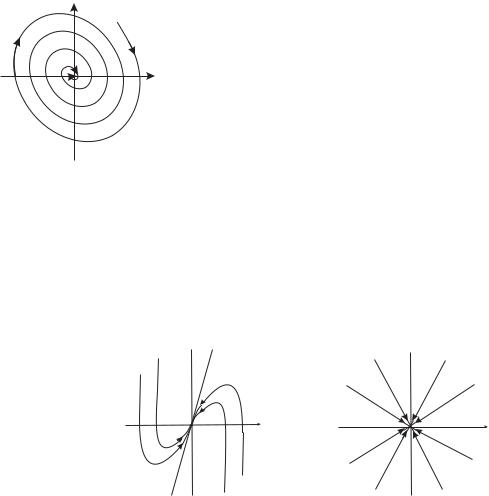
замене t → − t переходит в случай B2. Точки по спирали бегут от начала координат. Точка покоя называется неустойчивым фокусом.
y
C. Корни характеристического уравнения кратные: λ1 = = λ2 = λ. В этом случае решение системы имеет вид
x |
x(t) = (C1α1 + C2β1t)eλt , |
|
|
|
λt |
|
|
|
|
|
|
|
y(t) = (C1α2 + C2β2t)e , |
|
|
|
|
|
|
|
где |
C1 и C2 — произвольные постоянные. |
||
Рис. 13. Фокус |
|
|
|
C1. λ < 0. Пусть |
λ = −p 2. Тогда |
tlim x(t) = tlim y(t) = |
|
|
|
→∞ |
→∞ |
0. Точка покоя не только устойчива, но и асимптотически устойчива. Такая точка покоя называется вырожденным устойчивым
y 
 y
y
x |
x |
Рис. 14. Вырожденный узел |
Рис. 15. Дикритический узел |
узлом. Геометрически, вырожденный устойчивый узел занимает промежуточное положение между ситуациями A1 и B2, так как при сколь угодно малом изменении действительных коэффициентов a11, a12, a21, a22 она может превратиться как в устойчивый узел типа A1, так и в устойчивый фокус. Качественное поведение интегральных кривых в окрестности вырожденного узла показано на рисунке 14.
115

C2. При β1 = β2 = 0 получаем еще один тип устойчивого узла, так называемый дикритический узел (см. рисунок 15).
C3. λ > 0, пусть λ = p 2. При замене t → − t получим ситуацию C1 или C2. В данном случае, хотя интегральные кривые и сохраняют ту же форму, но точки вдоль них бегут в противоположном направлении. Имеем или вырожденный или
дикритический неустойчивый узел.
II. = 0. Случаи A, B, C исключают ситуацию, когда один из корней характеристического полинома является нулевым, ибо при рассмотрении этих случаев определитель ≡ (a11a22 − a12a21) = 0, а характеристическое уравнение имеет
вид λ2 − (a11 + a22)λ + |
= 0. D. Пусть теперь |
= 0 и |
λ2 − (a11 + a22)λ = 0. Тогда |
λ · [λ − (a11 + a22)] = 0 |
и, следова- |
тельно, возможны два решения: λ1 = 0 и λ2 = a11 + a22 = 0. Общее решение системы уравнений в рассматриваемой ситуации имеет вид
x(t) = C1α1 + C2β1eλ2t , |
|
|
λ2t |
|
|
|
|
y(t) = C1α2 + C2β2e . |
|
|
|
|
|
Исключим из этих двух уравнений переменную t, получим
y − C1α2 |
= |
β2 |
, |
|
|||
x − C1α1 |
|
β1 |
|
то есть имеем семейство прямых
β2(x − C1α1) − β1(y − C1α2) = 0,
которое при любых значениях C1 является семейством прямых,
|
|
x = C1α1, |
|
|
|
|
|
параллельных друг другу. При C2 |
|
то |
|
= 0 имеем |
|||
α2 |
|
y = C1α2, |
|
|
|
|
|
есть y = α1 |
|
|
|
x − целая прямая точек покоя. |
|
||
116

D1. λ2 < 0. Пусть λ = −q 2.
При t → ∞ точки на каждой траектории приближаются к точке покоя x = c1α1, y = c1α2. Точка покоя x = 0, y = 0 является точкой устойчивости, но асимптотической устойчивости нет.
|
|
D2. λ2 > 0. Пусть |
λ = q 2. |
|
y |
При замене |
t → − t |
приходим к случаю D1. |
|
|
||||
|
Однако при |
λ = q 2 движение происходит в про- |
||
|
x |
|
|
|
|
тивоположном направлении и точка покоя x = |
|||
|
0, |
y = 0, как и множество точек покоя, лежащих |
||
|
|
|
α |
|
|
на прямой y = α2 x, неустойчива. |
|||
|
|
|
1 |
|
Рис. 16. |
|
На рисунке 16 схематично изображено рас- |
||
положение траекторий около прямой точек покоя. Стрелками показано направление движения по траекториям при возрастании t.
E. Осталось рассмотреть последний случай, когда оба корня характеристического уравнения равны нулю: λ1 = 0, и λ2 = 0.
При этом a11 + a22 = 0, |
|
= a11a22 − a12a21 = 0. |
|
|
|
|||||||||||||
Положим |
a11 |
≡ a, |
|
тогда |
a22 |
= |
|
− a. Из |
|
= 0 |
||||||||
следует |
a |
a21 |
≡ ν, |
|
то есть |
|
|
|
|
a |
|
− νa. В |
||||||
|
= |
− |
|
|
a12 |
= |
|
|
, a21 |
= |
||||||||
a12 |
a |
|
ν |
|||||||||||||||
терминах этих обозначений наша система запишется в виде: |
||||||||||||||||||
x˙ = ax + ν ay, |
|
|
dy |
|
|
|
νx + y |
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|||||
|
|
|
|
|
dx |
|
− |
1 |
|
|
|
|||||||
|
|
|
|
или |
= |
|
|
|
|
= |
ν. |
|||||||
|
|
|
|
|
|
x + /ν y |
|
|||||||||||
y˙ = −νax − ay, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
E1. x = C1, |
y = C2. |
|
Каждая точка на плоскости есть |
|||||||||||||||
точка покоя. Все решения устойчивы.
117

E2. x = C1 + C2t, y = C3 + C4t, где C3, C4 – линейные комбинации C1, C2. Точка покоя x = 0, y = 0 не является устойчивой.
y
Пример 1. Особой точкой (седлом) системы уравнений
|
y˙ = 2x + y, |
|
x |
|
|
|
x˙ = 3x + 4y |
|
|
|
|
|
|
|
|
является точка (0, 0). Изображение интеграль- |
|
Рис. 17. Седло |
ных кривых в окрестности этой точки получе- |
|
но численным интегрированием системы в пакете |
||
|
"Математика"и приведено на рисунке 17. Две выделенные, хорошо видные на рисунке прямые — это сепаратриссы седла.
Пример 2. Особой точкой (фокусом) систе-
мы уравнений |
|
|
|
|
y |
|
|
|
|
|
|
|
y˙ = 4x − y, |
|
|
||
|
|
|
2y |
|
x |
|
x˙ = 3x |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является начало координат. Изображение интеграль- |
|
|
|||
ных кривых в окрестности этой точки получено чис- |
|
|
|||
ленным интегрированием системы в пакете "Мате- |
|
Рис. 18. Фокус |
|||
матика"и приведено на рисунке 18. |
|
|
|||
|
|
|
Пример 3. Особой точкой (вырожденным |
||
y |
узлом ) системы уравнений |
|
|||
|
|
||||
|
|
|
y˙ = x, |
|
|
|
|
|
|
|
|
|
x |
|
x˙ = 2x |
− |
y |
|
|
|
|
||
|
|
|
|
|
|
является точка (0, 0). На рисунке 19 показано расположение интегральных кривых, полученных численным интегрированием в пакете "Матема-
Рис. 19. Вырожденный узел тика". На рисунке хорошо видно единственное выделенное направление, отвечающее единственному кратному корню λ характеристического уравнения.
118

Пример 4. Особой точкой (центром) системы дифференциальных уравнений
y
y˙ = 2x + 2y, |
|
|||
|
|
|
|
|
x˙ = |
2x |
− |
5y |
x |
|
− |
|
||
|
|
|
|
|
является начало координат — точка (0, 0). На |
|
|||
рисунке 20 показано расположение интеграль- |
|
|||
ных кривых этой системы, полученных числен- |
|
|||
ным интегрированием в пакете "Математика". |
Рис. 20. Центр |
|||
Пример 5. Особыми точками системы
y |
|
|
дифференциальных уравнений |
|
|||
|
|
|
|
||||
2 |
|
|
y˙ = 4y2 |
− x2, |
|
|
|
|
|
|
|
|
|
|
|
2 1 |
4 |
x |
x˙ = 2xy |
− |
4e |
− |
8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
являются две точки: (−2, −1) и (4, 2). Пер- |
|
вая особая точка — фокус, вторая особая точка |
|
— узел. На рисунке 21 показано расположение |
Рис. 21. Узел + фокус |
интегральных кривых этой системы. Рисунок |
получен численным интегрированием в пакете "Математика". Пример 6. Особыми точками систе-
мы дифференциальных уравнений |
y |
|
y˙ = 4y2 |
− x2, |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x˙ = 2xy |
− |
4e |
− |
8 |
1 |
1 |
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
являются две точки: |
(−1, −1) и (1, 1). |
|
1 |
|
|||
Первая особая точка — седло, вторая осо- |
|
|
|
||||
бая точка — фокус. На рисунке 22 показа- |
|
|
|
||||
но расположение интегральных кривых этой |
Рис. 22. Фокус + седло |
||||||
системы. Рисунок получен численным интегрированием в пакете "Матема- |
|||||||
тика". |
|
|
|
|
|
|
|
Подводя итоги, заметим, что если оба корня характеристического уравнения имеют отрицательные вещественные части, то решение x = 0, y = 0 асимптотически устойчиво. Если хотя
119
бы один корень имеет положительную вещественную часть, то точка покоя x = 0, y = 0 неустойчива.
Совершенно аналогично обстоит дело и в случае системы
nлинейных однородных уравнений с постоянными коэффи-
циентами x˙ i = |
n |
aikxk, (i = 1, 2, ..., n), где A = |
|
aik |
|
|
|
|
|
||
|
k=1 |
|
|
|
|
— числовая матрица. Характеристическое уравнение для этой |
|||||
системы имеет вид |
det (A − λE) = 0. Если вещественные |
||||
части всех корней характеристического уравнения отрицательны, то точка покоя асимптотически устойчива. Если же вещественная часть хотя бы одного корня положительна, то точка
xi = 0 |
(i = 1, 2, ..., n) |
не является устойчивой точкой покоя. |
||||||||||
|
|
x˙ = 2y |
− |
z, |
|
|
− |
λ2 |
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2z, det (A |
|
3 λ 2 |
|||||
Пример. y˙ = 3x |
|
|
λE) = |
= |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
− |
− |
− |
||||
|
|
|
|
|
|
|
||||||
|
|
|
z˙ = 5x 4y. |
|
|
|
|
|
|
|
||
|
|
|
5 4 λ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
− |
|
|
|
− |
− |
|
||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= −λ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
+ 9λ − 8 = 0. У этого характеристического уравнения |
|||||||||||
существует положительный корень |
λ1 = 1 > 0. Точка покоя |
|||||||||||
неустойчива. |
|
|
|
|
|
|
|
|
|
|||
ЛЕКЦИЯ 16
16.1. Второй метод Ляпунова
Рассмотрим систему дифференциальных уравнений
dxi |
= f |
(t, x , x |
, ..., x |
n |
) (i = 1, 2, ..., n). |
(16.1) |
|
|
|
||||||
|
dt |
i |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1 (теорема Ляпунова об устойчивости.) Если су- |
|||||||
ществует дифференцируемая функция V (x1, x2, ..., xn), |
назы- |
||||||
120
