Данные проблемы можно решить при помощиоператора преобразования типа. Он может применяться явно или неявно. При преобразовании типа при необходимости может выполняться изменение самих данных преобразуемого объекта, но, по возможности, такой модификации следует избегать (недеструктивное преобразование). При преобразовании типа всегда создается новый объект целевого типа (иногда временный).

Для обеспечения возможности преобразования объекта классаАА к типу Т следует определить операторную функцию-член класса АА вида:

AA::operator T()

{

// Тело ...

}

Как видно, в прототипе этой функции не указан тип возвращаемого результата, т.к. этот тип является частью имени операторной функции. В этом отношении она имеет сходство с конструктором. Однако результат все же возвращается при помощи инструкцииreturn. Типом возвращаемого результата является тип Т. В имени функции между ключевым словом operator и именем целевого типа должен быть пробел.

Пусть требуется обеспечить возможность преобразования объекта классаComplex в указатель на тип double (в динамический массив объектов типаdouble). Тогда достаточно определить операторную функцию-член этого класса вида:

Complex::operator double *() const

{

double (*pvd)(new double[2]); pvd[0] = m_Re; pvd[1] = m_Im; return pvd;

}

В результате в программе становятся возможными, в частности, конструкции вида:

Т. о., если конструктор преобразует объект некоторого типа к своему классу, то оператор преобразования типа, наоборот, преобразует объект своего класса к некоторому типу.

4.4. перегрузка основных бинарных операторов

Оператор присваивания

Поскольку данный оператор изменяет содержимое своего первого операнда, то лучше его определять как член класса. Перегрузка оператора присваивания обязательна, если

среди объектов-членов его класса-владельца есть указатель на динамическую память.

Для класса Complex перегрузка оператора присваивания может выглядеть так(однако компилятор здесь справится с этим и сам, поэтому можно поручить присваивание ему):

Complex &Complex::operator=(const Complex cz)

{

m_Re = cz.m_Re; m_Im = cz.m_Im; return *this;

}

Для класса Vector перегрузка оператора присваивания может иметь вид:

Vector &Vector::operator=(const Vector &cv)

{

if (this != &cv)

{

delete[] m_pVec;

if (!(m_pVec = new double[m_Dim = cv.m_Dim]))

{

cout << "Ошибка! Недостаточно памяти." << endl; exit(-1);

}

size_t i;

for (i = 0; i < m_Dim; ++i) m_pVec[i] = cv.m_pVec[i];

}

return *this;

}

В любом случае данный оператор должен возвращать ссылку на объект-владелец вызова операторной функции, иначе будет невозможно использовать присваивание внутри выражений. Пример использования оператора:

Complex za(1, 2), zb, zc; Vector va(10), vb(5), vc; // ...

Составные операторы присваивания

Перегрузка данных операторов подобна таковой для оператора присваивания, т. к. при их выполнении также используются два операнда, и результат также сохраняется в объекте, являющемся первым операндом. Т. о., определять их лучше как члены класса.

В случае классаComplex составные арифметические операторы присваивания могут быть реализованы так:

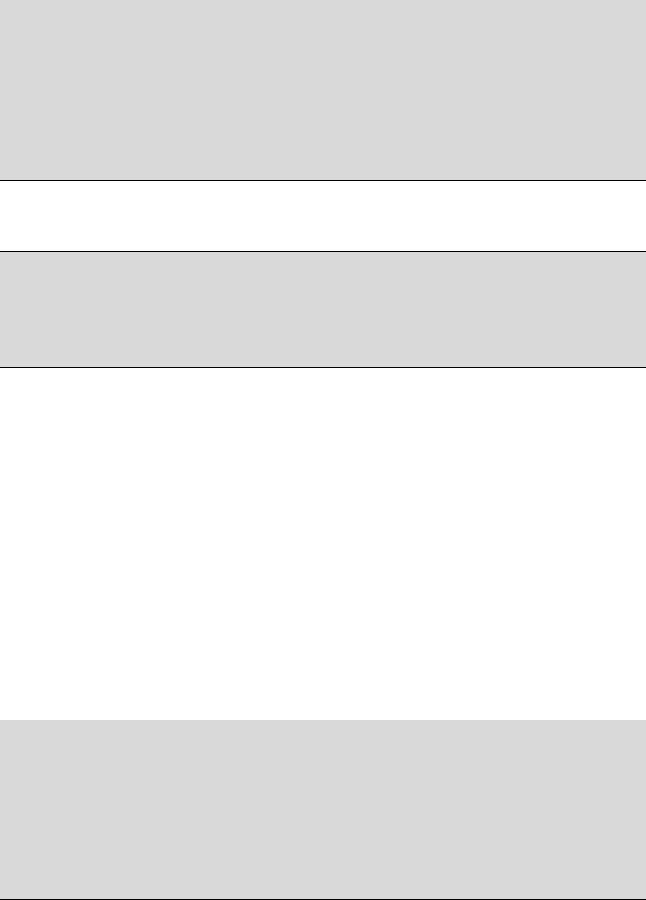
Complex &Complex::operator^=(const Complex cz) // Возведение в степень.

{

if (!m_Re && !m_Im) return *this;

Complex z(log(abs()), arg()); m_Re = m_Im = exp((z *= cz).m_Re); m_Re *= cos(z.m_Im);

m_Im *= sin(z.m_Im); return *this;

}

В случае классаVector составной оператор, например, умножения на число с последующим присваиванием может быть реализован так:

Vector &Vector::operator*=(const double cd)

{

size_t i;

for (i = 0; i < m_Dim; ++i) m_pVec[i] *= cd;

return *this;

}

Обычные арифметические и логические операторы

Как ни странно, данные операторы реализуются сложнее и выполняются дольше аналогичных им составных операторов присваивания. Вызвано это тем, что при их выполнении используется три объекта: два в качестве операндов и один в качестве результата выполнения операции, тогда как в составных операторах присваивания используется только два объекта: первый в качестве первого операнда, а также результата выполнения операции, и второй в качестве второго операнда. При этом для операторов без присваивания требуются сопутствующие операции копирования при создании объектов.

Поскольку обычные операторы не изменяют содержимого первого операнда, то соответствующие им операторные функции следует делать внешними.

Логические операторы обычно требуют доступа к закрытым элементам своих операндов, поэтому они, как правило, являются дружественными к классам этих операндов.

Арифметические операторы, как правило, не требуется делать дружественными, т. к. обычно они используют внутри себя соответствующие составные операторы присваивания.

Внешние операторные функции и обычные функции, не являющиеся дружественными к классам, но предназначенные для работы с их объектами, называют функциями-

помощниками этих классов.

В случае класса Complex обычные арифметические операторы могут быть реализованы как функции-помощники класса Complex следующим образом:

Complex operator+(const Complex cz1, const Complex cz2)

{

Complex temp(cz1); return temp += cz2;

}

Complex operator*(const Complex cz1, const Complex cz2)

{

Complex temp(cz1); return temp *= cz2;

}

Логические операторы сравнения объектов класса Complex должны быть определены как внешние функции, дружественные к классу Complex, например, так:

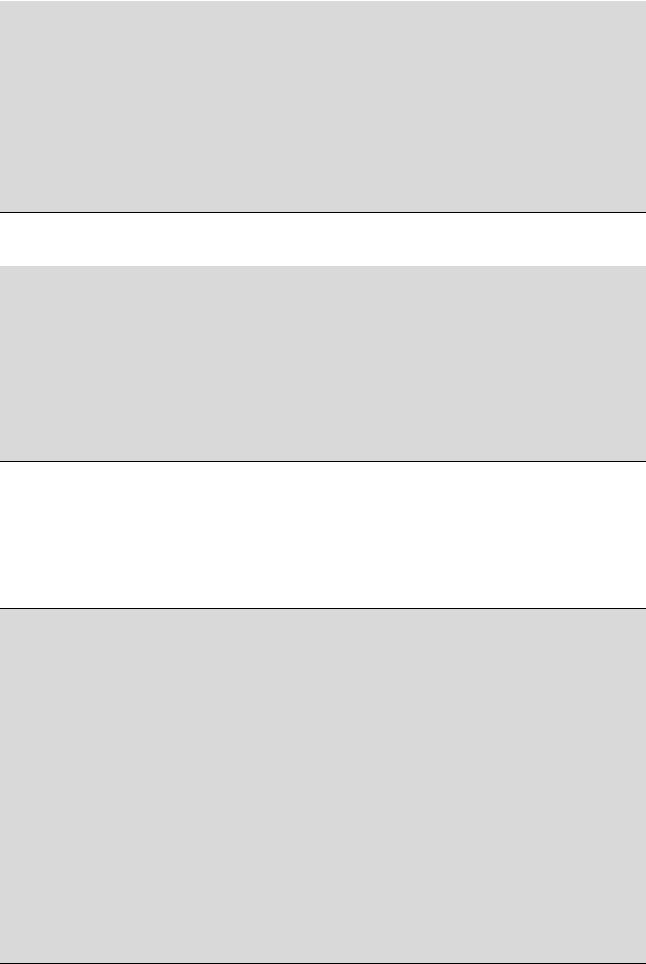
bool operator==(const Complex cz1, const Complex cz2)

{

if (cz1.m_Re == cz2.m_Re && cz1.m_Im == cz2.m_Im) return true;

return false;

}

bool operator!=(const Complex cz1, const Complex cz2)

{

if (cz1.m_Re == cz2.m_Re && cz1.m_Im == cz2.m_Im) return false;

return true;

}

Для класса Vector обычное арифметическое, например, умножение вектора на число может быть реализовано следующим образом:

Vector operator*(const Vector &cv, const double cd)

{

Vector temp(cv); return temp *= cd;

}

Vector operator*(const double cd, const Vector &cv)

{

Vector temp(cv); return temp *= cd;

}

Как видно, здесь потребовалась перегрузка обычного оператора умножения для поддержки коммутативности операции умножения вектора на скаляр.

Логический оператор сравнения объектов классаVector между собой, например, на равенство, а также логические операторы сравнения на равенство объекта классаVector с числом (и наоборот, числа с объектом класса Vector) должны быть определены как внешние функции, дружественные к классуVector. Таким образом этот оператор может быть перегружен в следующих вариантах:

bool operator==(const Vector &cv1, const Vector &cv2)

{

size_t Dim(cv1.m_Dim);

if (Dim != cv2.m_Dim) return false;

size_t i;

for (i = 0; i < Dim; ++i)

{

if (cv1.m_pVec[i] != cv2.m_pVec[i]) return false;

}

return true;

}

bool operator==(const Vector &cv, const double cd)

{

if (cv.m_Dim != 1) return false;

if (cv.m_pVec[0] != cd) return false; return true;

}