амплитудный спектр

Латыпов Р. К. 614 группа

Исследование амплитудных спектров сигналов

Цель работы: ознакомится аппаратурой, позволяющей анализировать амплитудный спектр Фурье периодических сигналов.

Выполнение работы:

На рисунке 1 приведена осциллограмма прямоугольного периодического импульса со скважностью Q = 3, и длительностью импульса Tи = 100 мкс. На рисунке 2 приведена его спектр, где экспериментальные значения обозначены символом “*”, а теоретические “x”.

Рис.1

Рис.2

1

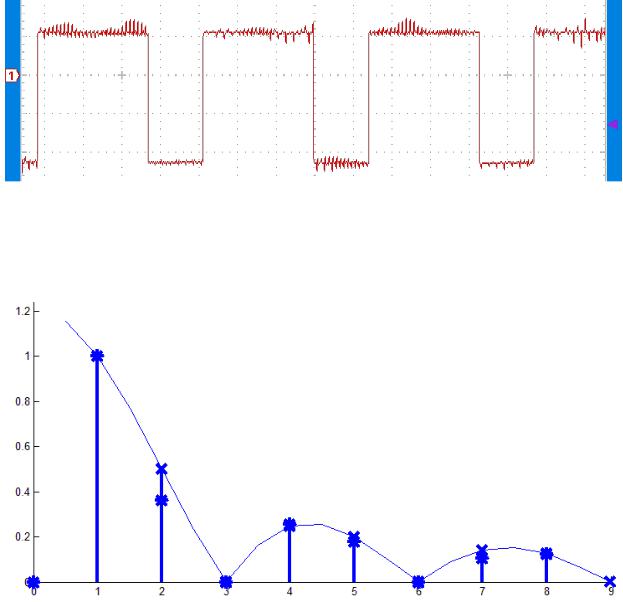
На рисунке 3 приведена осциллограмма прямоугольного периодического импульса со скважностью Q = 3, и длительностью импульса Tи = 140 мкс. На рисунке 4 приведена его спектр, где экспериментальные значения обозначены символом “*”, а теоретические “x”. Для импульсов с одинаковой скважностью амплитудный спектр значительно не отличается, то есть длительность импульса на амплитудный спектр не влияет. На рисунках 5 и 6 приведены осциллограмма прямоугольного сигнала со скважностью Q = 4 и амплитудный спектр сигнала.

Рис. 3

Рис. 4

2

Рис. 5

Рис. 6

Через схему дифференцирующей цепи

П(t) = Ϭ(t) - Ϭ(t- Tи)- уравнение прямоугольного импульса, где Ϭ(t)- единичная функция.

S(t) = уравнение прямоугольного сигнала при прохождении через схему дифференцирующей цепи.

Формула нормированного спектра амплитуд выходного сигнала для дифференцирующей цепи:

3

Где Kn – модуль комплексного коэффициента передачи дифференцирующей цепи

√

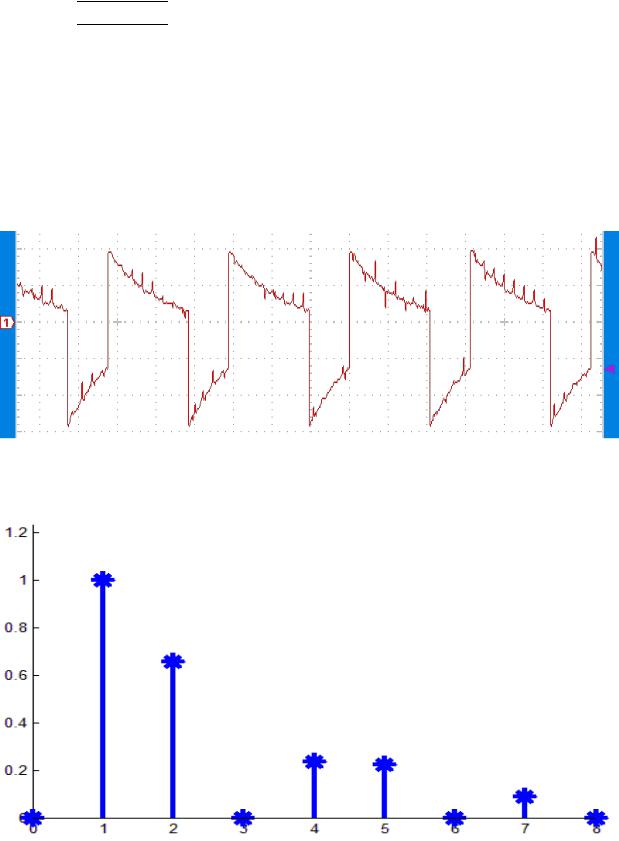
На рисунке 7 осциллограмма выходного сигнала дифференцирующей цепи при RC = Tи, на рисунке 8 его спектр. Из осциллограммы видно что дифференцирующая цепь является фильтром высокой частоты. Это хорошо видно на рисунках 9 и 10 при значении

RC = 0.1 * Ти.

Рис. 7

Рис. 8

4

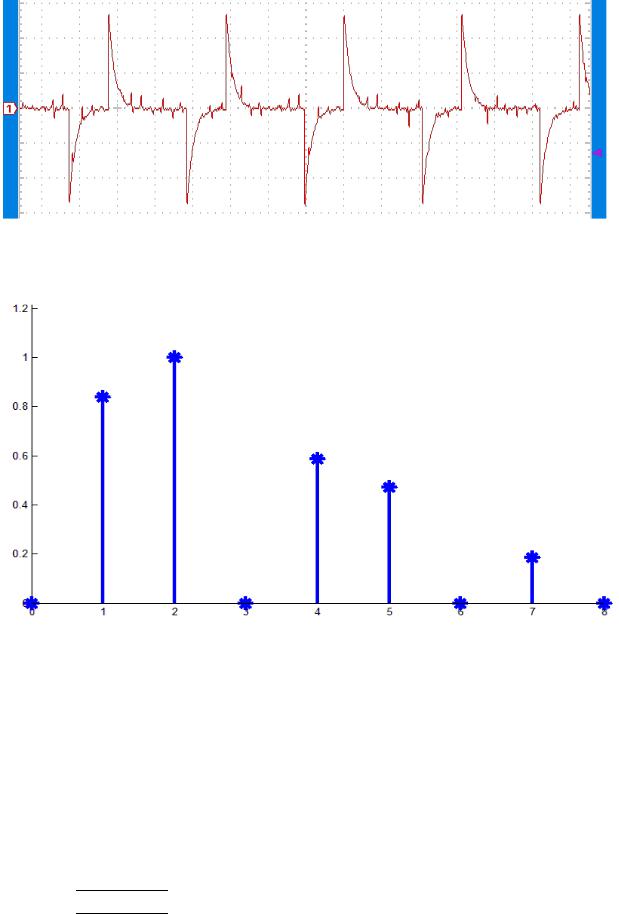
Рис. 9

Рис. 10

Через схему интегрирующей цепи

П(t) = Ϭ(t) - Ϭ(t- Tи)- уравнение прямоугольного импульса, где Ϭ(t)- единичная функция.

Формула нормированного спектра амплитуд выходного сигнала для интегрирующей цепи:

Где Kn – модуль комплексного коэффициента передачи дифференцирующей цепи

√

5

На рисунках 11, 12 осциллограмма выходного сигнала интегрирующей цепи при RC = Tи и его амплитудный спектр. Из осциллограммы видно, что фронт и срез прямоугольного сигнала сглажены, то есть интегрирующая цепь пропускает только низкие частоты. На рисунках 13 и 14 приведены осциллограмма выходного сигнала интегрирующей цепи при RC = 10*Tи и его спектр. При значении RC = 10*Tи у интегрирующей цепи наиболее хорошо выражены свойства фильтра низкой частоты.

Рис. 11

Рис. 12

Рис. 13

6

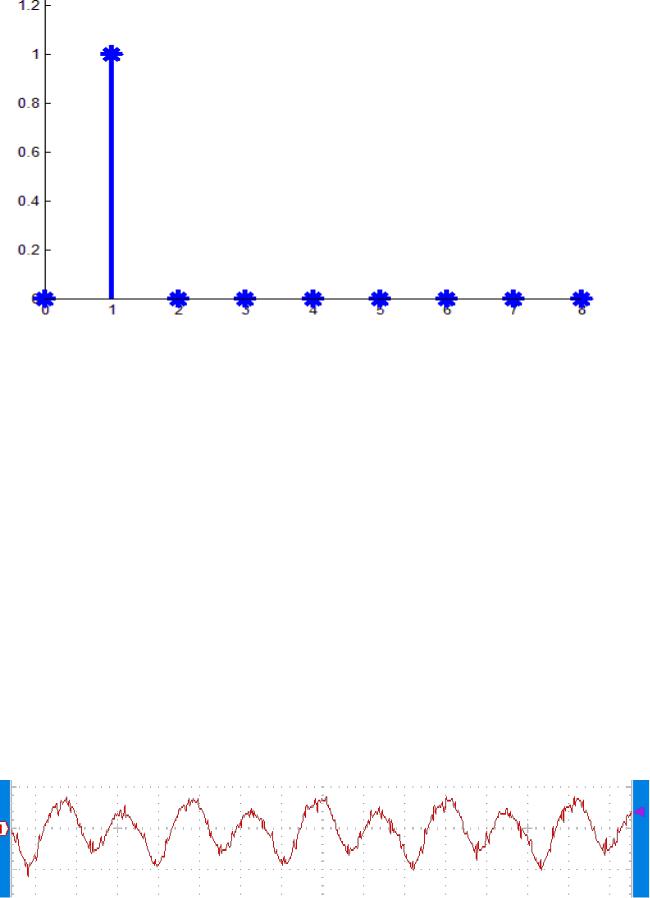
Рис. 14

Через схему полосового фильтра

Характеристики RLC цепи:

L = 2,7мГн, C = 0,1+0,01*6 = 0,16 мкФ

ωфильтр = 15,2 кГц

ω0 = 3,3 кГц

n = 4 - номер резонансной гармоники.

На рисунках 15, 16 приведены осциллограмма выходного сигнала полосового фильтра и спектр сигнала. Из спектра видно, что фильтр пропускает только до 4-ой гармоники

включительно. 4*ω0 = 13,2 кГц.

Рис. 15

7

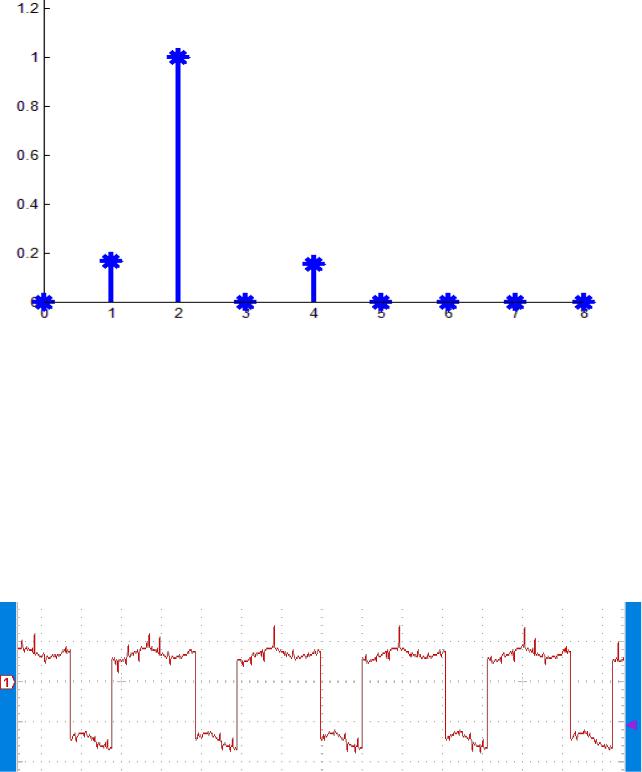
Рис. 16

Через схему режекторного фильтра

На рисунках 17, 18 осциллограмма выходного сигнала режекторного фильтра и его спектр. Из осциллограммы видно, что режекторный фильтр отфильтровывает средние частоты.

Рис. 17

8

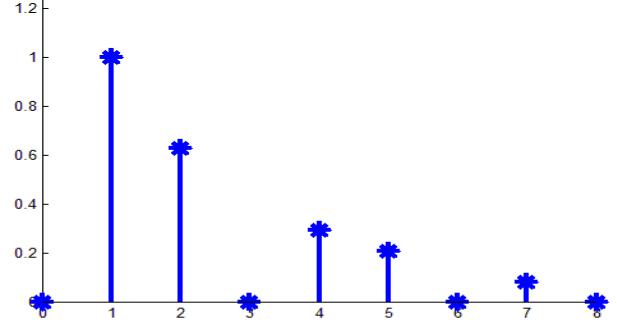
Рис. 18

9