Задание к расчетно-графической работе № 1 «Линейные электрические цепи с постоянными напряжениями и токами»:

Для заданной схемы с постоянными во времени источниками ЭДС и тока, принимая

e₁(t)=E₁, e₂(t) = E₂, e₃(t) = 0, j(t)=J,

выполнить следующее:

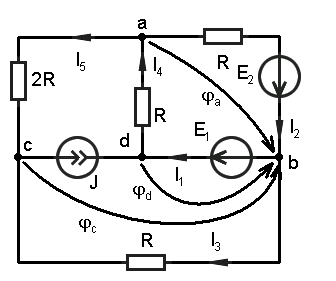
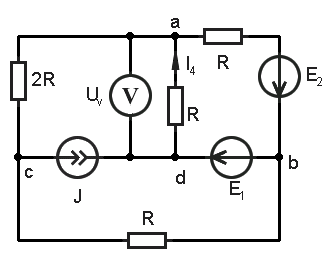
1. Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления.

2. Определить токи во всех ветвях схемы и напряжение на зажимах источника тока:

• по законам Кирхгофа,

• методом контурных токов,

• методом узловых потенциалов.

3. Составить баланс вырабатываемой и потребляемой мощностей.

4. Определить ток в ветви ab:

• методом наложения,

• методом преобразований.

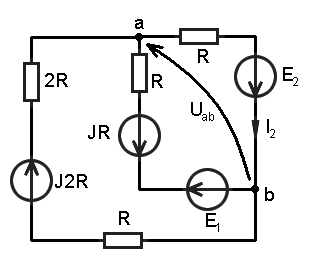
3. Рассматривая цепь относительно сопротивления R ветви аb как активный двухполюсник, заменить его эквивалентным генератором, определить параметры эквивалентного генератора и рассчитать ток в ветви ab, построить внешнюю характеристику эквивалентного генератора и по ней графически определить ток в ветви ab.

4. Для любого контура без источника тока построить потенциальную диаграмму.

5. Определить показание вольтметра.

8. Сравнить результаты вычислений, оценить трудоемкость методов расчета и сформулировать выводы по выполненным пунктам задания.

Исходные данные

E1 = 130 В; 1 = 45 град; E2 = 180 В; 2 = -45 град; J = 4 А;  = 180 град; R = 40 Ом; L = 127.39 мГн; С = 79.6 мкФ;

1. Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы, помеченные буквами, указав их номера и направления.

Т. к. в схеме действуют только источники постоянной энергии, то заменяем индуктивность на закоротку, а конденсатор на разрыв.

2. Определить токи во всех ветвях схемы и напряжение на зажимах источника тока используя законы Кирхгофа:

Записываем первый закон Кирхгофа для трех узлов: a, b, d

Записываем второй закон Кирхгофа для трех контуров: I₁₁, I₂₂, I₃₃

Выполняем подстановку:

Решаем систему в матричном виде:

Результаты расчета:

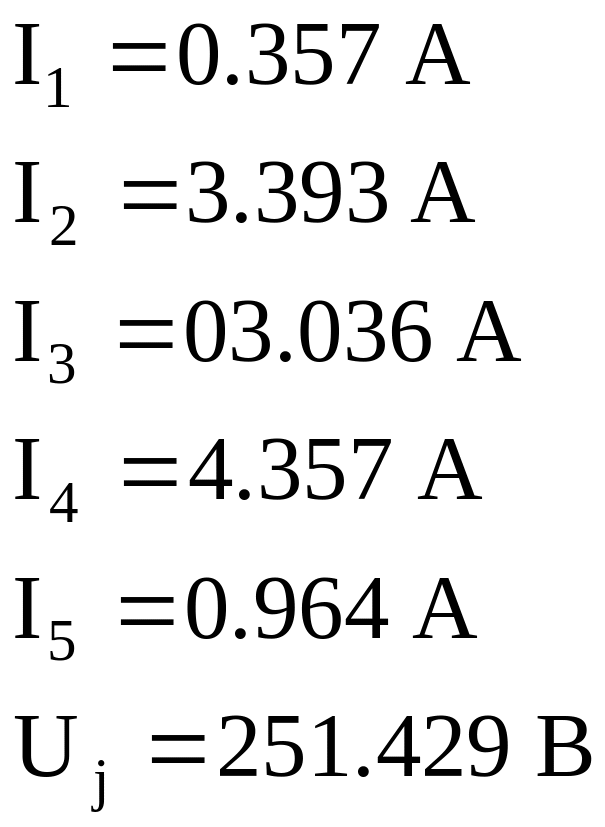
Определить токи во всех ветвях схемы используя метод контурных токов:

Записываем уравнения для двух контуров: I₁₁, I₃₃, при условии что I₂₂ = J:

Записываем систему в матричном виде находим её решение:

Результат расчета:

Определяем значения токов:

Определить токи во всех ветвях схемы используя метод контурных токов:

Заземляем узел d и записываем уравнения для узлов а, с, считая известным потенциал в узле d= E1:

Выполняем подстановку значений:

Записываем систему в матричном виде и рассчитываем ее:

Результат расчета:

Определяем значения токов в ветвях используя законы Кирхгофа:

3. Составить баланс вырабатываемой и потребляемой мощностей.

Определяем мощность источников энергии:

Определяем мощность потребителей энергии:

Определяем относительную погрешность расчета:

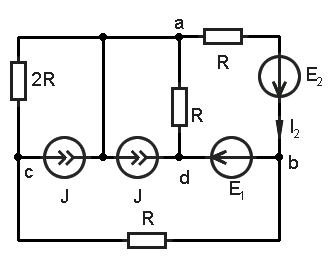
4. Определяем ток в ветви ab методом наложения.

Для определения тока в ветви данным методом, необходимо найти составляющие тока от каждого из источника энергии. При этом остальные источники ЭДС заменяются на закоротки, а источники тока на разрывы.

	Определяем эквивалентное сопротивление цепи относительно источника ЭДС E2 и находим составляющую тока в ветви ab: Определяем составляющую тока в ветви ab от источника ЭДС E1 c использованием метода разброса тока в параллельных ветвях:
	Используя правило разброса токов в параллельных ветвях определяем сначала ток , а затем тем же методом составляющую тока ветви ab:

Определяем ток в ветви ab как сумму составляющих от каждого из источников:

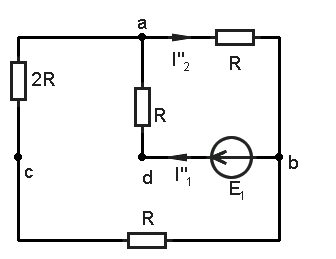
Определяем ток в ветви ab методом преобразования.

Преобразуем данную схему к схеме с двумя узлами. Для этого преобразуем источник тока в эквивалентные источники ЭДС в ветвях ca и ad. Методом двух узлов определяем напряжение между узлами ab: Используя второй закон Кирхгофа определяем ток Iab:

5. Определить показание вольтметра.

Т. к. вольтметр подключен параллельно сопротивлению в ветви ad, то показание вольтметра можно определить по закону Ома: Показание вольтметра 174.286 В.

6. Сравнить результаты вычислений, оценить трудоемкость методов расчета и сформулировать выводы по выполненным пунктам задания.

В результате выполнения задания №1 установлено, что результаты расчета не зависят от метода расчета, а зависят только от параметров схемы.

Метод уравнений Кирхгофа имеет большее по сравнению с другими методами количество уравнений, но простота составления уравнений, а также возможность расчета матрицы с помощью компьютера делают этот метод одним из удобнейших. Но если в схеме много ветвей и мало узлов и нет компьютера под рукой, то рациональнее всего использовать метод узловых потенциалов, и наоборот, узлов много, а ветвей мало, то удобнее использовать метод контурных токов. Если нас интересует только один ток во всей схеме, то наиболее рациональными могут оказаться метод наложения или преобразования. В случае использования метода наложения вообще не придется решать систему уравнений, но зато придется рассмотреть столько простых схем с одним источником энергии, сколько их находится в исходной схеме.

8