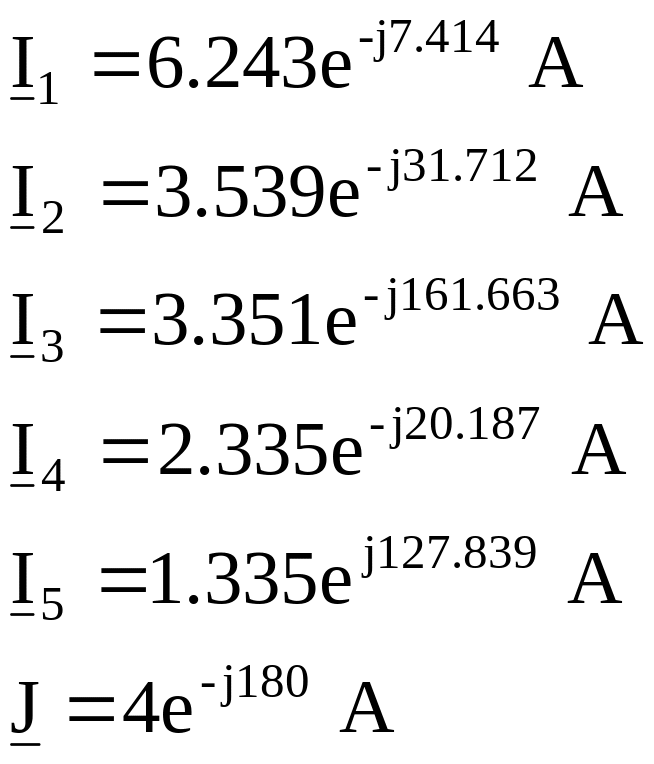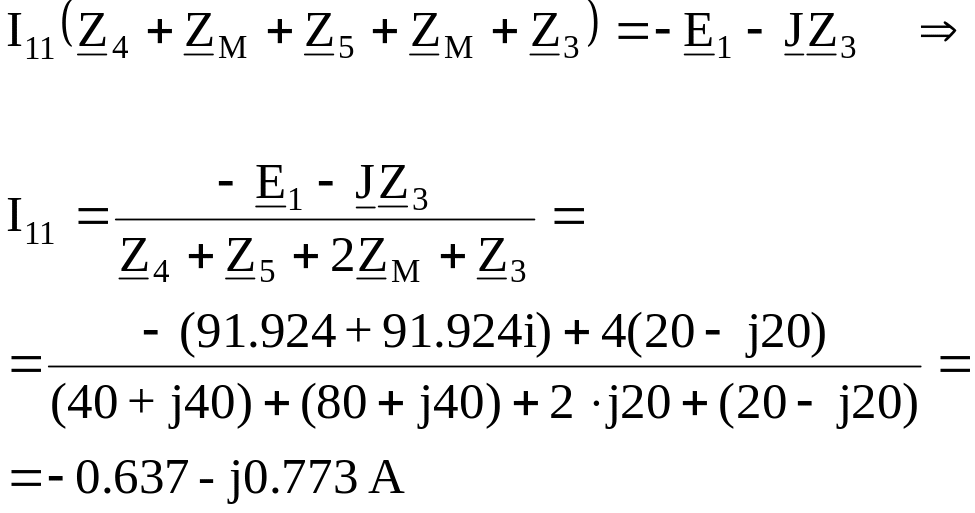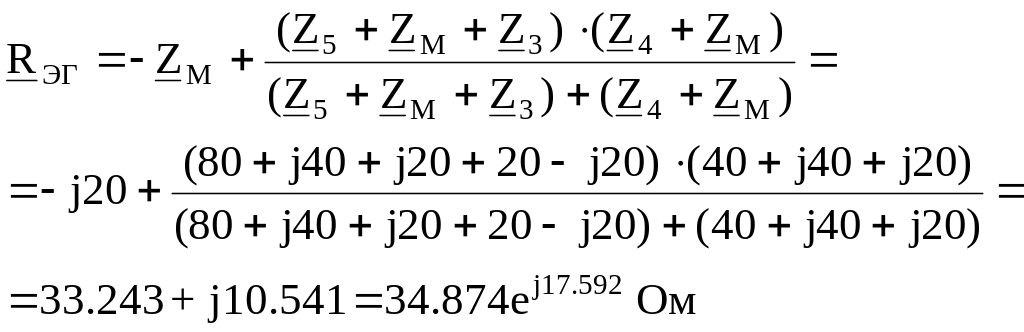349-2

ЗАДАНИЕ №2 Линейные электрические цепи с гармоническими напряжениями и токами.

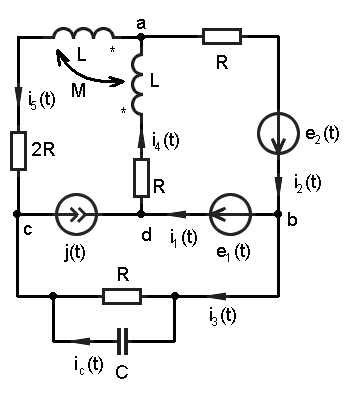
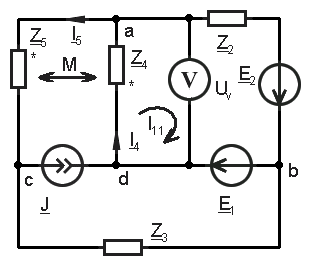
Для заданной схемы с источниками гармонических ЭДС и тока

принимая = 314 рад/с и M = L/2, выполнить следующее:

1. Записать систему независимых уравнений по законам Кирхгофа для мгновенных значений токов.

2. Рассчитать без учета М комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно заданию №1, причем параллельное соединение R и С представить в виде одного комплексного сопротивления).

3. Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока:

• по законам Кирхгофа,

4. Записать мгновенные значения тока в ветви ab и напряжения на зажимах источника тока.

5. Рассчитать балансы активной и реактивной мощностей.

6. Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжений.

7. Определить показание вольтметра.

8. Сделать развязку индуктивной связи и по методу эквивалентного генератора относительно сопротивления R ветви ab определить комплексное сопротивление активного двухполюсника (эквивалентного генератора) , ЭДС генератора E_Г и ток I_ab, в ветви ab, a затем при изменении сопротивления R ветви ab от 0 до 10 Z_Г рассчитать и построить зависимость для активной мощности P_ab = f (R).

9. Проанализировать результаты вычислений и сформулировать выводы по заданию.

1. Записать систему независимых уравнений по законам Кирхгофа для мгновенных значений токов.

Используя первый и второй законы Кирхгофа записываем систему независимых уравнений:

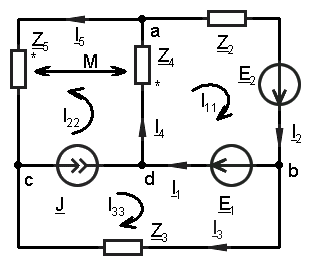
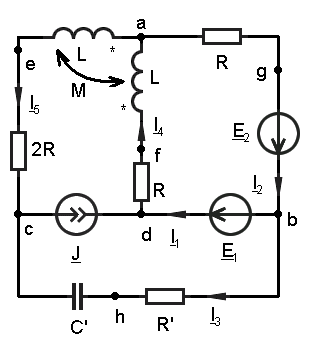
2. Рассчитать без учета М комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей.

Выполняем расчет сопротивлений реактивных элементов:

Выполняем расчет сопротивлений ветвей:

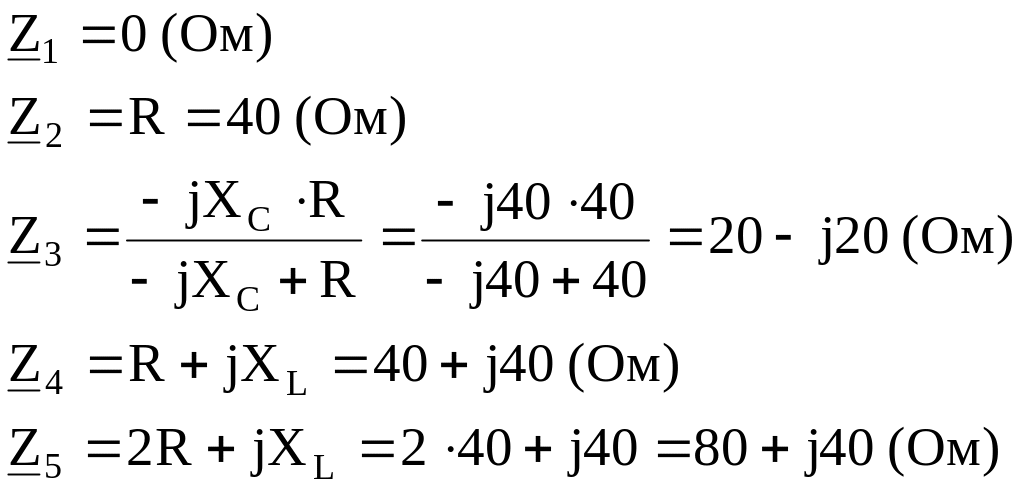
3. Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока по законам Кирхгофа.

Записываем систему уравнений по первому законам Кирхгофа:

Выполняем подстановку:

Записываем систему в матричном виде и решаем её:

Результаты расчета:

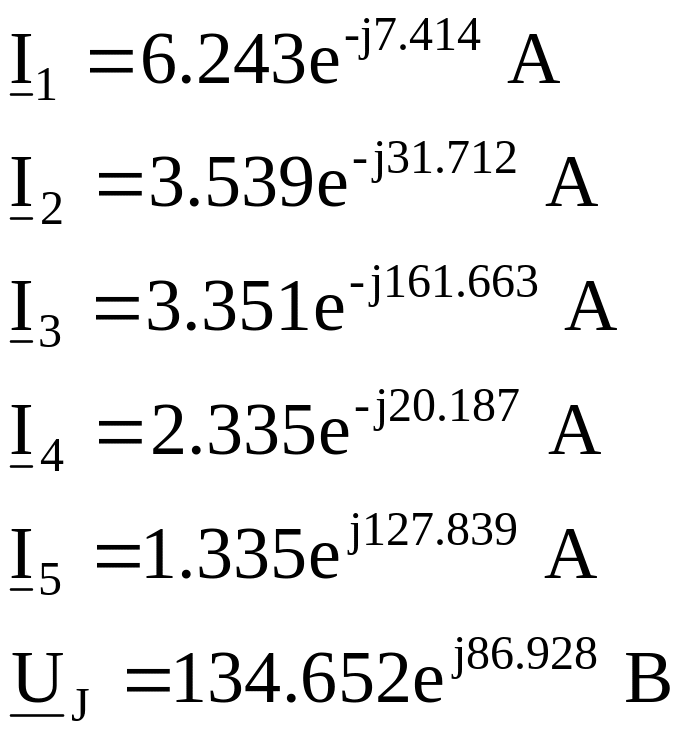
4. Записать мгновенные значения тока в ветви ab и напряжения на зажимах источника тока.

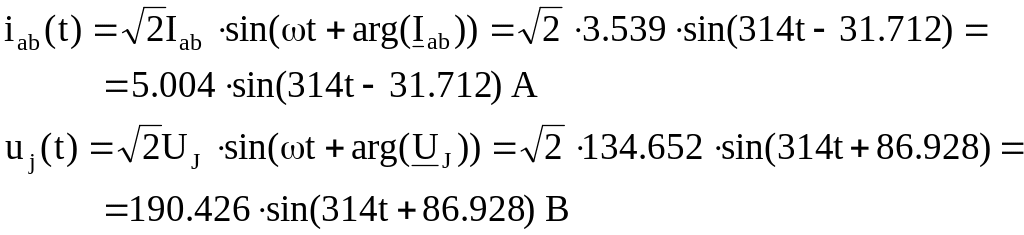
5. Рассчитать балансы активной и реактивной мощностей.

Определяем мощности источников энергии:

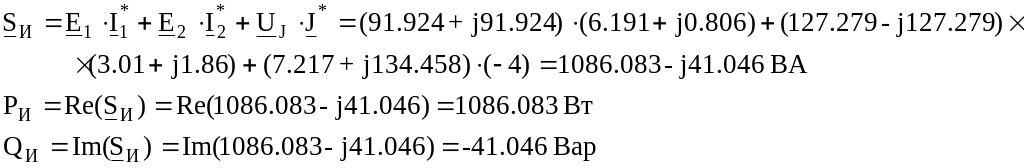Определяем активную мощность потребителей энергии и погрешность расчета:

Определяем реактивную мощность потребителей энергии и погрешность расчета:

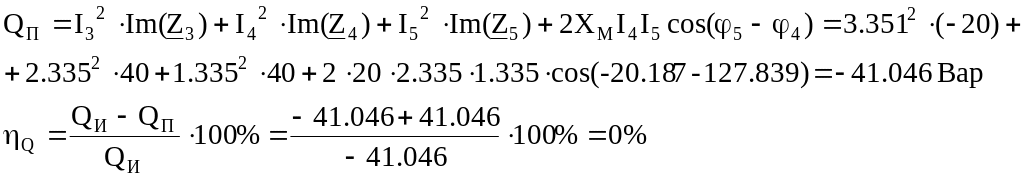
6. Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжений.

Выполняем расчет значений падений напряжений на всех элементах схемы:

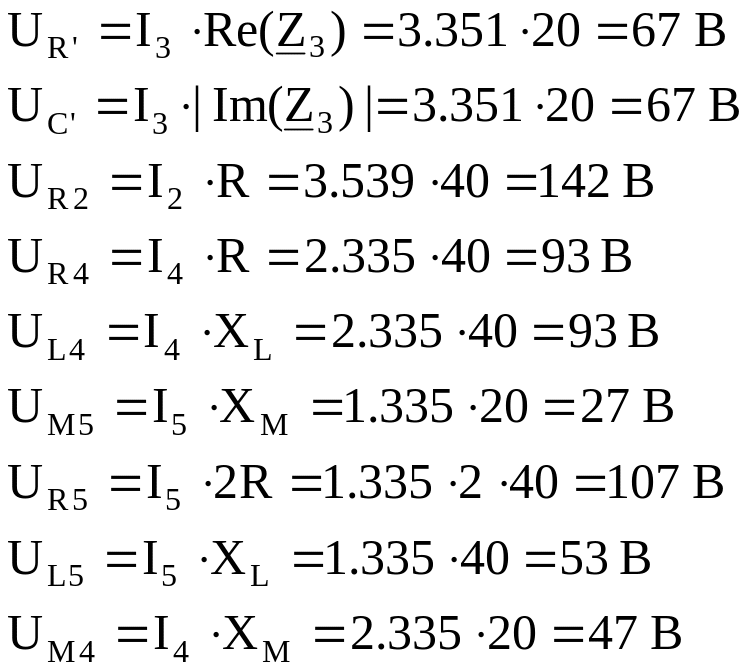
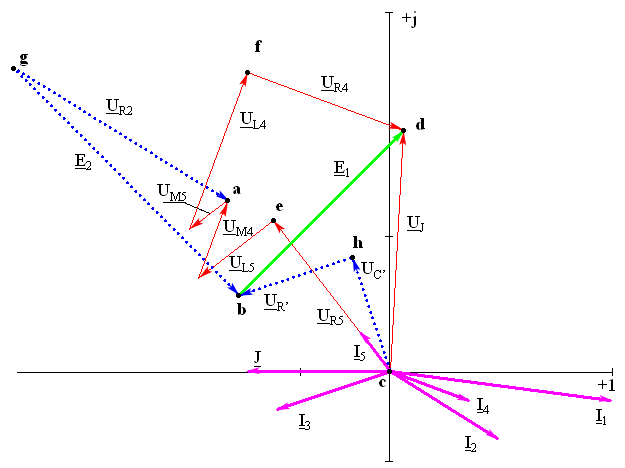
7. Определить показание вольтметра.

Определяем показание вольтметра по второму закону Кирхгофа из контура I11: Показание вольтметра 106.229 В.

8. Сделать развязку индуктивной связи и по методу эквивалентного генератора относительно сопротивления R ветви ab определить комплексное сопротивление активного двухполюсника (эквивалентного генератора) , ЭДС генератора E_Г и ток I_ab, в ветви ab, a затем при изменении сопротивления R ветви ab от 0 до 10 Z_Г рассчитать и построить зависимость для активной мощности P_ab = f (R).

Выполняем развязку катушек индуктивности и определяем напряжение холостого хода ЭГ при разомкнутой ветви ab:

Используя метод контурных токов записываем уравнение (I33 = J):

Из контура I₂₂ определяем U_xx:

Определяем сопротивление ЭГ. При этом все источники ЭДС заменяются на закоротки, а источники тока на разрывы:

Определяем ток в ветви ab:

Выполняем расчет зависимости активной мощности P_ab = f (R):

Задаемся значениями сопротивления R_ab от 0 до 3R_ЭГ, вычисляем ток в ветви ab, затем вычисляем активную мощность. Пример расчета для R_ab = R_ЭГ:

Сводная таблица значений:

Rab/RЭГ	-	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5
Rab	Ом	0	17,437	34,874	52,311	69,749	87,186	104,623	122,06	139,497	156,934
Iab	А	7,508	5,058	3,799	3,038	2,529	2,166	1,894	1,682	1,513	1,375
Pab	Вт	0	446,161	503,266	482,673	446,161	409,03	375,203	345,384	319,338	296,588

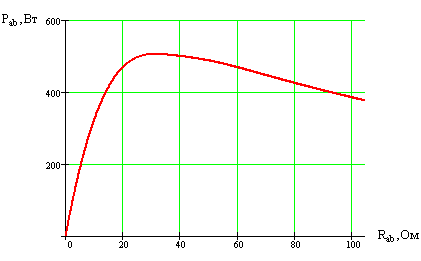
По результатам расчета строим зависимость для активной мощности P_ab = f (R).

9. Проанализировать результаты вычислений и сформулировать выводы по заданию.

Результатом выполнения задания №2 является расчет электрической цепи с гармоническим источниками энергии. Как и в предыдущем задании убедились, что результаты расчета не зависят от метода расчета, а также в том, что для схем с гармоническими источниками энергии справедливы все законы и методы расчета, используемые для расчета цепей постоянного тока. Согласно зависимости P_ab(R_ab) можно убедится, что наибольшая активная мощность в ветви ab выделяется в режиме согласованной нагрузки, т. е. когда сопротивление внешней цепи равно внутреннему сопротивлению источника.

По сравнению с цепями с постоянными источниками энергии, данное задание является более сложными и требует наличия персонального компьютера для выполнения расчетов, что обусловлено наличием реактивных элементов, а также взаимосвязи между катушками индуктивности.

10