3. Разбивка передаточного отношения по ступеням

Данный механизм состоит из двух ступеней:

Первая ступень – планетарная зубчатая передача вида АJ, состоит из зубчатых колес 2', 3, 4 и водила Н;

Вторая ступень – зубчатая передача внешнего зацепления, состоящая из зубчатых колес 1 и 2.

Передаточное отношение всего механизма определим как произведение всех передаточных чисел механизма:

;

где и - передаточное отношение планетарного механизма 1 и 2;

- передаточное отношение рядового механизма.

Примем передаточное отношение планетарного механизма и , тогда передаточное отношение планетарного механизма определим следующим образом

.

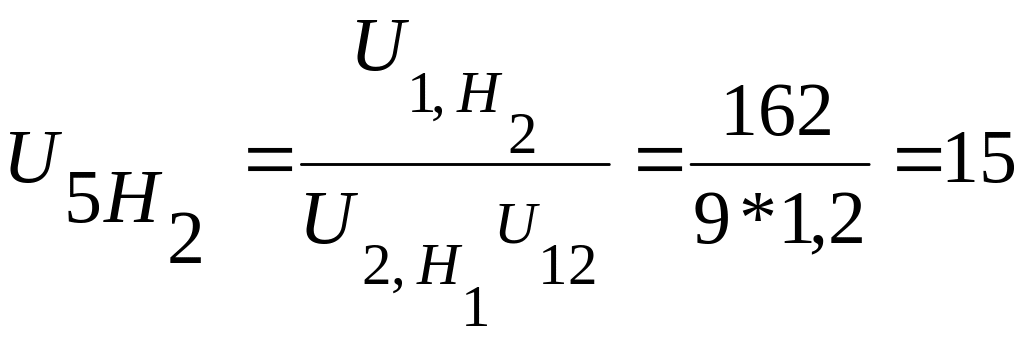4. Подбор чисел зубьев зубчатых колес

   Подберем число зубьев зубчатых колес, удовлетворяющих требуемому отношению, условию соосности, сборки и соседства по методу сомножителей. Так как передача осуществляется от колеса 1 к водилу Н и задано передаточное отношение , то передаточное отношение обращаемого механизма определим по формуле

Осуществим подбор зубьев для планетарного механизма типа АJ по формуле:

;

подставив в эту формулу полученное получим:

.здесь

;

выразим через числа зубьев:

.

Заменим числа зубьев пропорциональными им коэффициентами С, тогда

.

Запишем в таблицу 1 все возможные варианты разложения на сомножители виде дроби , где B =1 и варианты разложения с помощью дополнительных множителей учитывая рекомендации

Таблица 1

№ вариант	1	2	3	4	5	6

В соответствии с рекомендациями пределами отношения сомножителей при которых выполняется условие соседства смежных сотелитов исключаем из рассмотрения.

Определим P, Q и P+Q по формуле:

;

где , а значение С₁, С₂, С₂^I, С₃ берутся из таблицы 1 для соответствующего варианта.

Например для варианта 1 (С₁=2, С₂=6, С₃=19, С₂^I =3)

;

т.е. Р=1, Q=1, P+Q=2

Аналогично определяем P и Q для других вариантов, а результаты заносим в таблицу 2.

Таблица 2

	1	2	4	5	6
Р	16	5	18	18	6
Q	8	25	12	20	22
P+Q	24	30	30	38	28

Из таблицы следует, что минимальную сумму P+Q имеет вариант 1.

Определим числа зубьев зубчатых колёс для варианта 1 по формуле:

; ;

; ;

.

Подставив значения (С₁=2, С₂=6, С₂^I =3, С₃=19, Р=16, Q=8) приняв значение получим:

.

.

.

.

Определяем габариты и

после подстановки значений и и чисел зубьев имеем:

.

1. Проверка передаточного отношения

Проверяем выполнение заданного при принятом числе зубьев по формуле:

;

где n – число пар колес внешнего зацепления n =1

;

Заданное передаточное отношение выполняется.

2. Проверка выполнения условия соосности

Проверяем выполнение условия соосности по формуле:

,где , ,

Условие соосности выполняется.

3. Проверка условия сборки

Проверяем условие сборки по формуле:

;

где К_2.2=2 (число сателлитов), D_2.2=24 (наибольший общий делитель зубьев Z₂ и Z₂^I )

- целое число

Условие сборки выполняется.

Поскольку выполнены рекомендации, то условие соседства можно не проверять.

4. Подбор чисел зубьев для рядового механизма

Передаточное отношение рядового механизма вычисляется по формуле:

,

где и - числа зубьев рядового механизма.

Примем число зубьев для шестерни , тогда число зубьев для колеса

.

5. Геометрический расчёт внешнего эвольвентного зацепления

Для зубчатых колёс 4,5 выполняется полный геометрический расчёт, который приведен в таблице 3. Коэффициенты смещения приняты из условия износостойкости.