3.1. Зубчатый механизм
При проектировании планетарного механизма по выбранной схеме и заданному передаточному отношению подобрать числа зубьев колёс, при которых получились бы наименьшие размеры механизма.
Выбранные числа зубьев колёс планетарного механизма должны удовлетворять следующим основным условиям:
обеспечению заданного передаточного отношения;
соосности центральных зубчатых колёс;
возможности сборки механизма;
соседству смежных сателлитов;
правильному зацеплению каждой пары зубчатых колёс.
.1. Разбивка передаточного отношения
Исходные данные:
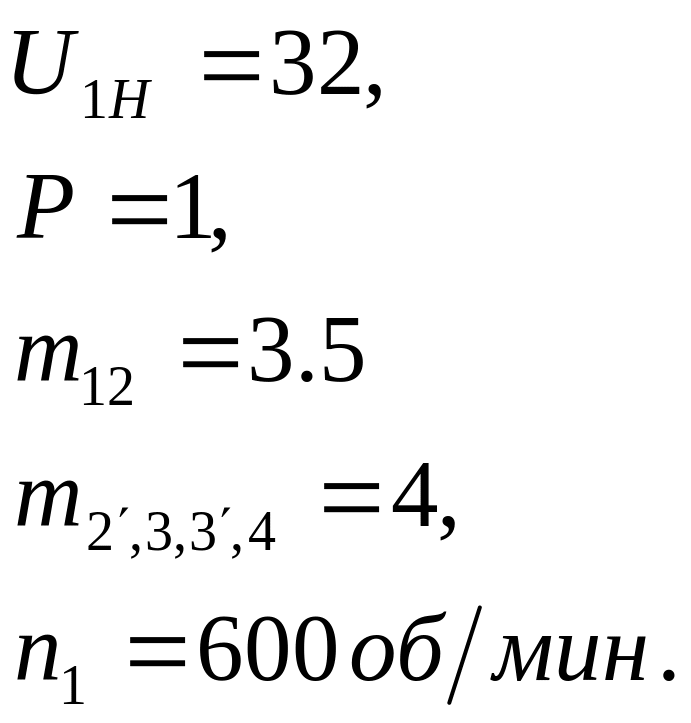
Схема механизма.
Данный механизм состоит из планетарного механизма типа АА и рядового механизма.
Подбор чисел зубьев
Осуществим подбор зубьев для планетарного механизма типа АА при
следующих данных:
Примем .
Зубчатые колёса прямозубые.
1.1.3. Определение передаточного отношения обращённого механизма
.
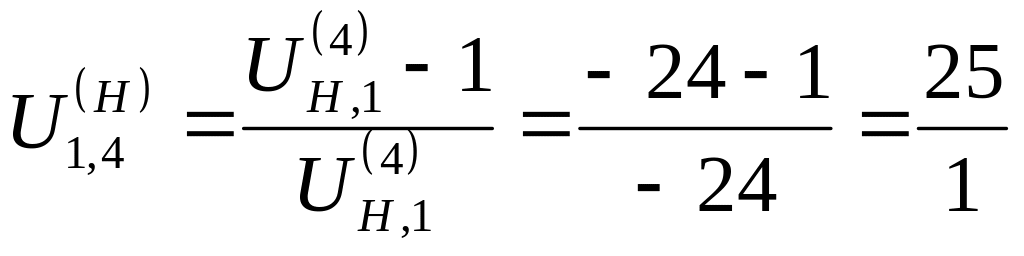Запишем в таблицу
1 все возможные варианты разложения
на сомножители.
.
№ вариантов разложения |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
Определим P, Q, P+Q по формуле 23
,
где
,
а значение
берутся из таблицы 1 для соответствующего
варианта.
Например, для
варианта 1 (
)
,
т.е.
Аналогично определяем P и Q для других вариантов, а результаты заносим в таблицу 2.
Таблица 2.
|
1 |
2 |
3 |
4 |
5 |
Р |
6 |
6 |
6 |
6 |
6 |
Q |
6 |
30 |
30 |
30 |
30 |
P+Q |
12 |
36 |
36 |
36 |
36 |
Из таблицы видно, что P+Q минимальную сумму имеет вариант 1.
1.1.4. Определение чисел зубьев зубчатых колёс
Определим числа зубьев зубчатых колёс для варианта 2 по формулам:
;
,
;
.
Подставив значения ( ) получим:
;
,
;
.
Примем
,
получим:
,
,
,
.
Для сравнения проводим аналогичные расчёты для вариантов: 4, 5, 7.
Результат заносим в таблицу 3.
Таблица 3
№ варианта разложения |
сомножители |
Z2 |
Z3 |
Z3 |
Z4 |
Условие сборки |
Габариты (мм) |
||||
С2 |
С3 |
С3 |
С4 |
Г1 |
Г2 |
||||||
1 |
1 |
5 |
1 |
5 |
18 |
90 |
18 |
90 |
Вып. |
792 |
792 |
4 |
5 |
5 |
1 |
25 |
90 |
90 |
18 |
450 |
Вып |
990 |
990 |
5 |
1 |
5 |
5 |
25 |
18 |
90 |
90 |
450 |
Не вып |
990 |
990 |
По таблице 3 видно, что наименьшие габариты выдаёт вариант 1:
, , , , .
Передаточное отношение
Передаточное отношение определяется по формуле:
.
Условие соосности
Это условие
обеспечивается при точном равенстве
межосевых расстояний (
)
соответствующих пар зубчатых колёс:
откуда
,
,
.
Условие сборки
,
где К3,3=1, D3,3=18.
Условие соседства не проверять (т.к. пользовались таблицей для определения передаточного отношения).
Условие сборки удовлетворяется.
Геометрические параметры внешнего эвольвентного зацепления цилиндрических прямозубых колёс, нарезанных инструментом реечного типа
Таблица 4
Исходные данные |
|||||
Параметры |
Обозначение |
Величина |
|||
Число зубьев |
шестерни |
Z1 |
12 |
||
колеса |
Z2 |
16 |
|||
Модуль зацепления, мм |
m |
3,5 |
|||
Исходный контур по ГОСТ 13755 - 68 |
Угол профиля, град |
|
20 |
||
Коэффициент высоты головки |
|
1 |
|||
Коэффициент радиального зазора |
С* |
0,25 |
|||
Коэффициент радиуса кривизны переходной кривой |
|
0,38 |
|||
Коэффициент cмещения |
|
А |
X1 |
0,45 |
|
X2 |
0,44 |
||||
Б |
X1 |
0 |
|||
X2 |
0 |
||||
РАСЧЕТ
Формула |
Наименование параметра |
|
А |
Б |
||
1 |
Передаточное число |
|
1,333 |
1,333 |
||
2
|
Эвольвентный угол в точке на делительной окружности |
|
|
|||
|
||||||
3 |
Эвольвентный угол в точке на начальной окружности
|
|
0,035438 |
0,014904 |
||
4 |
Угол зацепления, град. |
|
|
0,4921 |
0.364 |
|
|
W |
0.8972 |
0.9397 |
|||
5
|
Делительный шаг зубьев, мм |
P=
|
10,996 |
10,996 |
||
6 |
Основной шаг зубьев,мм |
|
10,333 |
10,333 |
||
7
|
Начальный шаг Зубьев, мм |
|
11,516 |
10,996
|
||
8 |
Межосевое расстояние,мм |
|
51,319 |
49 |
||
9 |
Радиус делительной окружности, мм |
|
21
28 |
21
28 |
||
10 |
Радиус основной окружности, мм |
|
18,200
26,312 |
18,200
26,312 |
||
11 |
Радиус начальной окружности, мм |
|
21,994
|
21
|
||
29,325 |
28 |
|||||
12 |
Радиус окружности впадин, мм |
|
19,734
24,815 |
16,625
23,625 |
||
13 |
Радиус окружности вершин, мм |
|
25,629
32,244 |
25
32 |
||
14 |
Угол профиля на окружности вершин |
|
39,65
0,8287 35,312
0,7083 |
36,35
0,7358 73,356
0,6583 |
||
15 |
Эвольвентный угол в точке на окружности вершин |
|
0,136691
0,092038 |
0,101460
0,076099 |
||
16 |
Толщина зуба по дуге делительной окружности, мм |
|
6,644
6,364 |
5,498
5,498 |
||
17 |
Толщина зуба по дуге основной окружности,мм |
|
6,832
6,764 |
5,754
5,951 |
||
18 |
Толщина зуба по дуге начальной окружности, мм |
|
6,055
5,461 |
5,498
5,498 |
||
19 |
Толщина зуба по дуге окружности вершин, мм |
|
1,866
2,354 |
2,173
2,330 |
||
20 |
Высота зуба, мм |
h= |
7,429 |
7,88 |
||
21 |
Глубина захода, мм |
h3=h-c* |
6,554 |
7 |
||
22 |
Показатель заострения |
|
0,553
0,673 |
0,621
0,666 |
||
23 |
Коэффициент воспринимаемого смещения |
|
0,662 |
0 |
||
24 |
Воспринимаемое смещение |
ym |
2,319 |
0 |
||
25 |
Коэффициент уравнительного смещения |
|
0,128 |
0 |
||
26 |
Радиус кривизны перехода кривой |
|
1,33 |
1,33
|
||
26| |
Радиальный зазор, мм |
c=c*m
|
0,88 |
0,88 |
||
27 |
Аналитический коэффициент перекрытия |
|
1,19 |
1,46 |
||
=0,014904
=0,3639
=0,9397
17’36”
W
0
-
