1. Булевы функции. Основные логические операции. Штрих Шеффера и стрелка Пирса. Выразимость одних операций через другие.

B = {0, 1}.

Булева функция — функция f : B^n → B.

Литерал — любая переменная x или ее отрицание x.

σ ^σ = x если σ = 1 и !x если σ = 0.

σ ^σ = 1 и σ^!σ = 0 для всех σ ∈ B.

Таким образом, x^σ = 1 тогда и только тогда, когда x = σ. А также, x^σ = 0 тогда и только тогда, когда x != σ, то есть x = !σ.

1. константа 0,

2. константа 1,

3. f1(x) = x – тождественная функция,

4. f2(x) = !x – отрицание x (читается как «не x»),

5. f3(x, y) = x & y – конъюнкция x, y (читается как «x и y» и иногда обозначается через x ∧ y),

6. f4(x, y) = x ∨ y – дизъюнкция x, y (читается как «x или y»),

7. f5(x, y) = x → y – импликация x и y (читается как «из x следует y»),

8. f6(x, y) = x + y – исключающее ИЛИ от x и y,

9. f7(x, y) = x/y – функция Шеффера от x и y.

Стрелка Пирса

—отрицание

—конъюнкция

—дизъюнкция—импликация

-(X∨Y), 1+X+Y+XY;

Штрих Шеффера

—отрицание

—дизъюнкция

—конъюнкция

—константа 1

-(X*Y), 1+XY;

2. ДНФ и КНФ. Теоремы о совершенных ДНФ и КНФ.

Конъюнкция нескольких литералов называется элементарным конъюнктом

Примеры -

Элементарный конъюнкт называется полным, если он содержит все рассматриваемые переменные.

Дизъюнкция нескольких литералов называется элементарным дизъюнктом

Примеры -

Элементарный дизъюнкт называется полным, если он содержит все рассматриваемые переменные.

Дизъюнкция нескольких элементарных конъюнктов называется дизъюнктивной нормальной формой (ДНФ). Пример -

Дизъюнкция нескольких полных элементарных конъюнктов называется совершенной дизъюнктивной нормальной формой (СДНФ).

Конъюнкция нескольких элементарных дизъюнктов называется конъюнктивной нормальной формой (КНФ). Пример -

Конъюнкция нескольких полных элементарных дизъюнктов называется совершенной конъюнктивной нормальной формой (СКНФ).

Теорема. Для любой булевой функции f : B^n → B имеет место

Доказательство. Пусть f(x1, x2, . . . , xn) = 1. Тогда при σ1 = x1, σ2 = x2, . . . , σn = xn имеем

Поэтому правая часть (п.ч.) равна 1.

Пусть п.ч. равна 1. Тогда для некоторого (σ1, σ2, . . . σn) ∈ B^n , такого, что f(σ1, σ2, . . . σn) = 1, имеем

Значит для каждого значение, а это возможно только при xi = σi. Таким образом, f(x1, x2, . . . , xn) = 1.

Теорема. Для любой булевой функции f : B^n → B имеет место

Доказательство. Пусть f(x1, x2, . . . , xn) = 0. Тогда при σ1 = x1, σ2 = x2, . . . , σn = xn имеемПоэтому правая часть (п.ч.) равна 0.

Пусть п.ч. равна 0. Тогда для некоторого (σ1, σ2, . . . σn) ∈ B^n, такого, что f(σ1, σ2, . . . σn) = 0, имеем. Значит для каждогозначение, а это возможно только при xi = σi. Таким образом, f(x1, x2, . . . , xn) =0.

3. Минимальные ДНФ. Импликанты и простые импликанты, сокращенные ДНФ и тупиковые ДНФ. Алгоритм нахождения минимальной ДНФ.

ДНФ наименьшего веса называется минимальной. Весом ДНФ называется количество литералов,

входящих в ДНФ.

Элементарный конъюнктназываетсяимпликантом булевой функции, если , для всех x1, x2, . . . , xn∈ B.

Если K присутствует в ДНФ функции f, то K является импликантом f.

Импликант функции f называется простым импликантом, если ни одна его собственная часть не

является импликантом f.

Теорема. Каждый элементарный конъюнкт в минимальной ДНФ для булевой функции f является простым импликантом.

Доказательство. Пустьявляется минимальной ДНФ. Докажем, что K1 (например) является простым импликантом. Пусть не так: существует импликант K’, являющийся собственной частью K1. Тогдато есть получили ДНФ, с меньшим весом чем минимальная. Противоречие.

Следствие. Пусть P — множество всех простых импликантов булевой функции f. Тогда.

Доказательство. Пустьминимальная ДНФ. Тогда

Дизъюнкция всех простых импликантов функции f называетсясокращенной ДНФ.

Пусть P — множество всех простых импликантов f. ДНФ вида где S⊆ P, называется тупиковой ДНФ, если для имеем

Теорема. Минимальная ДНФ является тупиковой.

Доказательство. Пусть минимальная ДНФ для f. Ясно, что весбудет еще меньше при

Нахождение минимальной ДНФ.

1. Строим сокращенную ДНФ.

2. Последовательно удаляем лишние конъюнкты из сокращенной ДНФ, находим все тупиковые ДНФ.

3. Находим минимальную ДНФ, выбирая тупиковую ДНФ с наименьшим весом.

?4. Монотонные функции. Теорема о сокращенной ДНФ для монотонных функций. Композиция монотонных функций есть снова монотонная функция.

Набор (x1, x2, . . . , xn) ∈ B^n меньше или равен набору (y1, y2, . . . , yn) ∈ B^n ,

(x1, x2, . . . , xn) ≤ (y1, y2, . . . , yn), если x1 ≤ y1, x2 ≤ y2, . . . , xn ≤ yn.

Функция f : B^n → B называется монотонной, если

(x1, . . . , xn) ≤ (y1, . . . , yn) ⇒ f(x1, . . . , xn) ≤ f(y1, . . . , yn)

для всех (x1, x2, . . . , xn),(y1, y2, . . . , yn) ∈ B^n.

0, 1, x, y, x ∨ y, x & y — монотонные функции.

Теорема. Простые импликанты монотонных функций не содержат отрицаний.

Доказательство. Пусть — простой импликант монотонной функцииf(x1, x2, . . . , xn) при k ≤ n. Тогда

Значит Таким образомЗначит,импликант f, а это противоречит

тому, что — простой импликант.

Теорема. Сокращенная ДНФ монотонной функции является тупиковой (и, следовательно, минимальной).

Доказательство. Пусть K = x1 & . . . & xk — простой импликант f(x1, x2, . . . , xn), k≤n, f=K∨f’, где f’—

дизъюнкция всех простых импликантов f, кроме K.

Докажем, что f != f’. Заметим, что каждый импликант K’ != K должен содержать литерал xi,i > k, так как K — простой. Поэтому, при .

Имеем Значит, f != f’.

5. Многочлен Жегалкина. Представимость булевых функций многочленами Жегалкина.

Определение. Многочленом Жегалкина называется сумма нескольких элементарных конъюнктов без отрицаний.

Примеры. 0, 1, xy, 1 + x, x + y, x + y + xy, 1 + x + xy + xyz,

Теорема. Любая булева функция f : B^n → B представляется в виде многочлена Жегалкина, причем единственным образом

Доказательство существования. Представим f в СДНФ

Заметим, что при имеем

ПоэтомуТаким образом, достаточно доказать, что любой элементарный конъюнктпредставляется в виде многочлена Жегалкина. Без ограничений общности можно считать, что

Тогда, где суммирование проводится по всем конъюнктам K без отрицаний от переменных x1, x2, . . . xk.

Доказательство единственности. Пусть и f1, f2, . . . , fN— все булевы функции от n аргументов. Пусть Gi —количество различных многочленов Жегалкина функции fi,

В силe доказанного Gi ≥ 1, Тогда для количества G всех многочленов Жегалкина от n аргументов имеем

поскольку всего существует только 2^n конъюнктов без отрицаний, каждый из которых может входить или не входить в многочлен. Поэтому, Gi = 1 для каждого , то есть каждаяfi имеет только один многочлен Жегалкина

6. Замкнутые классы булевых функций. Классы T_0 и T_1. Классы монотонных, линейных и самодвойственных функций.

Пусть M - некоторое множество булевых функций. Множество [M], состоящее из всех функций, представимых формулами над M, называется замыканием M.

Определение. Класс функций C ⊆ F называется замкнутым, если [C] = C, то есть каждая формула над C принадлежит C.

Примеры

• Класс всех функций F — замкнутый. В силу Предложения 4 любое замыкание [C] является

замкнутым классом.

• M = [{0, 1, ∨, &}] — класс монотонных функций.

• L = [{0, 1, +}] — класс линейных функций, состоящих из многочленов Жегалкина вида a0 + a1x1 + · · · + anxn, где ai ∈ B.

Теорема. Класс T_0, состоящий из всех f ∈ F, для которых f(0, . . . , 0) = 0, является замкнутым.

Док-во. Пусть f, A1, . . . , An ∈ T_0 и g = f(A1, . . . , An). Тогда g(0, . . . , 0) = f(A1(0, . . . , 0), . . . , An(0, . . . , 0)) = f(0, . . . , 0) = 0, так что g ∈ T_0. Т.к. A1, . . . , An ∈ замкнутому классу, то g = f(A1, . . . , An) тоже замкнут.

Теорема. Класс T1, состоящий из всех f ∈ F, для которых f(1, . . . , 1) = 1, является замкнутым.

Док-во. Пусть f, A1, . . . , An ∈ T1 и g = f(A1, . . . , An). Тогда g(1, . . . , 1) = f(A1(1, . . . , 1), . . . , An(1, . . . , 1)) = f(1, . . . , 1) = 1, так что g ∈ T1. Т.к. A1, . . . , An ∈ замкнутому классу, то g = f(A1, . . . , An) тоже замкнут.

Теорема. Класс S, состоящий из всех f ∈ F, для которых (-f(x1, . . . , xn)) = f(-x1, . . . ,- xn),

является замкнутым.

Доказательство. Пусть f, A1, . . . , Ak ∈ S и g = f(A1, . . . , An).

Тогда (-g(x1, . . . , xn)) =[- f(A1(x1, . . . , xn), . . . , Ak(x1, . . . , xn))] =

= f([-A1(x1, . . . , xn)], . . . ,[- Ak(x1, . . . , xn))] = f(A1(-x1, . . . , -xn), . . . , Ak(-x1, . . . , -xn)) = g(-x1, . . . , -xn),

так что g ∈ S. Т.к. A1, . . . , An ∈ замкнутому классу, то g = f(A1, . . . , An) тоже замкнут.

7. Полные классы функций. Теорема Поста о полноте (доказательство теоремы слева направо).

Определение. Класс функций C ⊆ F называется полным,

если [C] = F. (если замыкание этого класса равно классу всех булевых функций)

Примеры.

- {∨, &, }, {∨, }, {&, }, {1, +, ·}, {|}, {↓} — полные

классы.

- {0, 1, ∨, &}, {0, 1, +} — неполные классы.

Теорема (критерий Поста). Теорема. Класс функций C ⊆ F является полным тогда и

только тогда, когда C не содержится в классах T0, T1, M, L,S.

Доказательство. Пусть система функций B является полной. Допустим, что B

содержится в одном из перечисленных замкнутых классов, который обозначим

через A. Тогда [B] ⊆ [A] = A. В силу полноты системы B, класс A содержит

все булевы функции. Противоречие.

8. Лемма о несамодвойственной функции. Лемма о немонотонной функции.

Лемма. Если f S ,то 0, 1 ∈ [{f,}].

Док-во. Пусть f S .Тогда существует набор (σ1, . . . , σn) такой, что Тогда

Поэтому для формулы имеем

Таким образом, одна из констант 0, 1 является формулой над {f, }. Подставляя ее в отрицание, получим другую константу.

Лемма о немонотонной функции : Если fM ,то я∈ [{f, 0, 1}].

Пусть fM.Тогда существует наборы (σ1, . . . , σn) ≤ (τ1, . . . τn) такие, что f(σ1, . . . , σn) = 1 и

f(τ1, . . . τn) = 0. Определим формулы

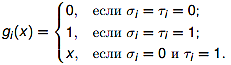
Тогда gi(0) = σi и gi(1) = τi для всех i = 1,..,n. Поэтому для формулы h(x) = f(g0(x), . . . , gn(x)) имеем h(0) = 1 и h(1) = 0, то есть h(x) =x.

9. Лемма о функциях, не сохраняющих t_0 и t_1. Теорема Поста о полноте (доказательство теоремы справа налево).

Лемма. Если f T0и g T1,то либо ∈ [{f, g}], либо 0, 1 ∈ [{f, g}].

Доказательство. Имеем f(0, . . . , 0) = 1 и g(1, . . . , 1) = 0. Если f(1, . . . , 1) = 0, то f(x, . . . , x) =x и лемма доказана. Пусть теперь f(1, . . . , 1) = 1. Тогда f(x, . . . , x) = 1 и, следовательно, 1∈ [{f, g}].

Остается показать, что 0 ∈ [{f, g}]:

Следствие. Если f T0, gT1, pSи qM ,то либо, 0, 1 ∈ [{f, g, p}], либо , 0, 1 ∈ [{f, g, q}].

Теорема (критерий Поста). Теорема. Класс функций C ⊆ F является полным тогда и

только тогда, когда C не содержится в классах T0, T1, M, L,S.

Док-во. Обратно, пусть B содержится в одном из пяти вышеперечисленных классов.

Выделим в B систему функций fT0, fT1, f S , f M , f L, не принадлежащих классам

T0 , T1 , S , M и L соответственно. Не ограничивая общности можно считать, что каждая из этих функций зависит от фиксированного числа переменных x1, . . . , xn .Покажем, что при помощи функций fT0, fT1 и fS можно получить константы 0 и 1. Если fT0(1, . . . ,1) = 1, то функция ϕ(x) = fT0(x, . . . , x) тождественно равна 1, поскольку ϕ(0) = 1 = ϕ(1). Константа 0 получается из fT1, поскольку

fT1(1, . . . ,1) = 0. Если же fT0(1, . . . ,1) = 0, то ϕ(x) = fT0(x, . . . , x) = !x, поскольку ϕ(0) = fT0(0, . . . ,0) = 1 и ϕ(1) = fT(1, . . . ,1) = 0. По лемме 10 при помощи x и fS можно получить константу. Вторая константа получается применением x. при помощи констант 0, 1 и функции fM можно получить !x. Наконец, по лемме 12 при помощи констант 0, 1 и функций !x и fL можно получить x1 & x2 . Теперь полнота системы B следует из полноты конъюнкции и отрицания. Неполный класс функций A назовем предполным, если класс A ∪ {f} будет

полным для любой функции f 6∈ A.

10. Неориентированные графы. Степени вершин. Сумма степеней вершин графа. Изоморфизм графов. Пример неизоморфных графов с одинаковыми степенями.

Определение. Неориентированный граф состоит из множества вершин V и множества ребер E, причем каждому ребру e ∈ E сопоставлена неупорядоченная пара вершин a, b.

Определение. Ребро, сопоставленное паре {a, a} называется петлей. Если несколько ребер сопоставлены одной и той же паре вершин {a, b}, то такие ребра называют кратными.

Определение. Неориентированный граф (V, E) называется простым, если среди элементов V нет петель и кратных ребер. Для случая простых графов мы будем отождествлять ребра e ∈ E с соответствующей парой вершин {a, b} ∈ V^2.

Определение. Если ребру e ∈ E сопоставлена пара вершин {a, b} ∈ V^2, то будем говорить, что ребро e инцидентно каждой из вершин a и b.

Определение. Если имеется ребро e ∈ E, сопоставленное паре вершин {a, b} ∈ V^2, то будем говорить, что вершины a и b являются смежными.

Определение. Степенью вершины deg(j) неориентированного графа называют количество инцидентных вершине j ребер, при этом каждая инцидентная ей петля считается два раза. Другими словами, deg(j) =

Теорема. Сумма степеней всех вершин неориентированного графа равна удвоенному количеству ребер,

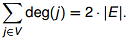
Доказательство.

Определение. Неориентированные графы G = (V, E) и G’ = (V’, E’) изоморфны, если существуют биективные отображения f : V → V’ и g : E → E’ такие, что e ∈ E инцидентна a ∈ V ⇐⇒ g(e) ∈ E’ инцидентна f(a) ∈ V’.

Для случая простых графов для изоморфизма достаточно существования биективного отображения f : V → V’ такого, что

a, b ∈ V — смежные ⇐⇒ f(a), f(b) ∈ V’ — смежные.

Для изоморфных графов G и G’ имеем deg(a) = deg(f(a)).