1.3. Упражнения и задачи

Задача 1.3.1

Так называемая кривая Филипса описывает связь темпа роста заработной платы и уровня безработицы. А именно,

,

где – уровень заработной платы,- темп роста заработной платы (в процентах) и– процент безработных в годt. Теория предполагает, что <0 и >0.

Используя данные для некоторой страны из таблицы

1. найдите оценки коэффициентов уравнения и проверьте наличие значимой связи между 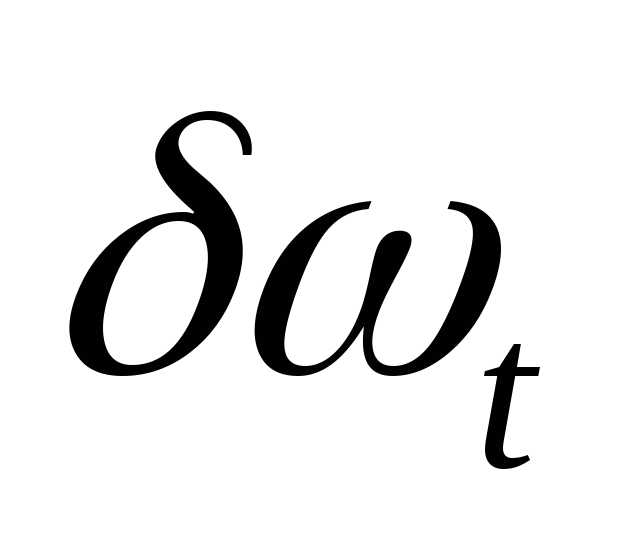и;

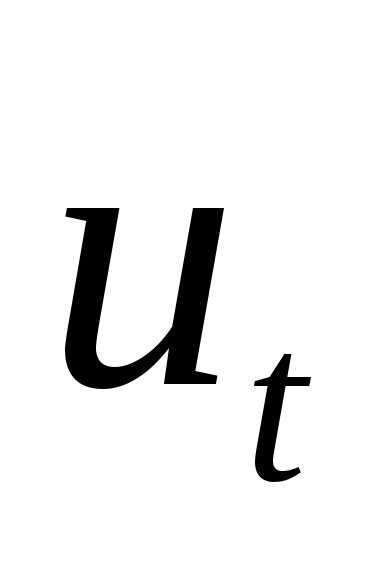2. найдите «естественный уровень безработицы», т.е. такой уровень безработицы, при котором 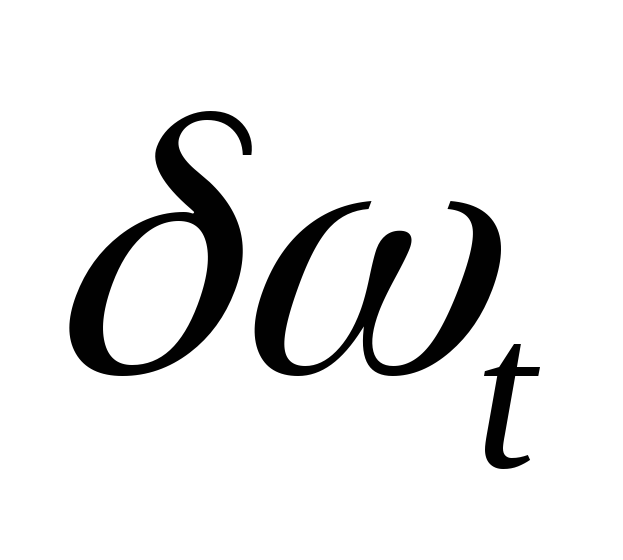= 0;

3. когда изменения в уровне безработицы оказывали наибольшее (наименьшее) влияние на темп изменения заработной платы;

4. найдите 95% – доверительные интервалы для и.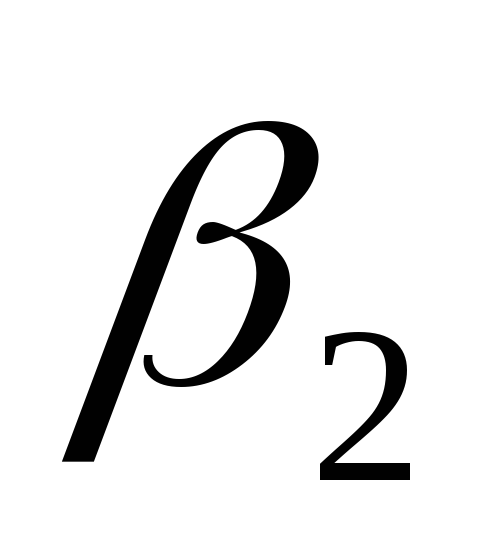

Год			Год
1	1,62	1,0	10	2,66	1,8
2	1,65	1,4	11	1,73	1,9
3	1,79	1,1	12	2,80	1,5
4	1,94	1,5	13	2,92	1,4
5	2,03	1,5	14	3,02	1,8
6	2,12	1,2	15	3,13	1,1
7	2,26	1,0	16	3,28	1,5
8	2,44	1,1	17	3,43	1,3
9	2,57	1,3	18	3,58	1,4

Задача 1.3.2

Для 14 однотипных предприятий (i – номер предприятия) имеются данные за год (см. табл.)

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14
yi	20	24	28	30	31	33	34	37	28	40	41	43	45	48
xi	32	30	36	40	41	47	56	54	60	55	61	67	69	76

y_i – производительность труда, т/ч;

x_i – уровень механизации работ, %.

Требуется:

1. Построить выборочное уравнение линейной парной регрессии (найти значения b₁ и b₀);

2. Рассчитать значение выборочного коэффициента корреляции rxy., среднюю ошибку аппроксимации, выборочный коэффициент детерминации R2 и стандартные отклонения коэффициентов регрессии;

3. На уровне значимости α=0,05 оценить значимость коэффициентов и уравнения регрессии, проверить значимость линейной функции регрессии Найти доверительные интервалы для значимых коэффициентов регрессии и значений yi;

4. Оформить выводы в виде аналитической записки.

Задача 1.3.3

Имеются следующие статистические данные по Республике Татарстан:

Год	2001	2002	2003	2004	2005	2006	2007
Зарегистрировано преступлений, yi	71266	57632	58866	63529	922324	105105	81251
Общая численность безработных, xi	116144	99669	125714	137444	126825	107042	108327

Требуется:

5. Определить по МНК оценки коэффициентов уравнения регрессии.

6. Проверить статистическую значимость коэффициентов, входящих в уравнение регрессии.

7. Найти доверительные интервалы для коэффициентов регрессии при уровне значимости = 0,05.

8. Рассчитать коэффициент детерминации и на уровне значимости 0,05 проверить значимость линейной функции регрессии с помощью F-критерия Фишера.

9. Найти точечное (с надёжностью 0,95) предсказание зависимой переменной при значении объясняющей переменной, равном максимальному наблюдённому её значению, увеличенному на 10%.