2. Физические приложения двойного интеграла

I. Вычисление массы плоской фигуры

Пусть на плоской фигуре Р распределена масса m. Поверхностной плотностью массы в точке N фигуры Р называется предел

,

где D – произвольный участок фигуры Р содержащий точку N, его площадь также обозначим D, m(D) – его масса. Условие DN означает, что участок D стягивается к точке N, то есть наибольшее расстояние от точки N до точек участка D стремится к нулю.

Если плотность распределена равномерно по фигуре, то (х;у)=const .

Задача. Вычислить массу плоской фигуры Р, по которой непрерывным образом распределена масса m с поверхностной плотностью (х;у), при этом (х;у)- непрерывная функция.

Разобьём фигуру сетью кривых на n произвольных частей: Р₁,Р₂,…,P_n, площади которых тоже обозначим Р₁,Р₂,…,P_n, а m₁,m₂,…,m_n - их массы. В каждой части P_i возьмем произвольно точку N_i(u_i;v_i) и вычислим в ней плотность (u_i;v_i). Если разбиение достаточно мелко, то в силу непрерывности функция (х;у) мало изменяется в области P_i. Следовательно, можно считать, что . Тогда .

Равенство тем точнее, чем мельче разбиение, и становится точным в пределе при где , _i=diamP_i.

Так как (х;у)-непрерывная функция, то предел справа существует и равен . Следовательно,

m= .

II. Вычисление статических моментов и центра тяжести плоской фигуры

С татический момент М материальной точки массы m относительно некоторой оси равен произведению массы этой точки на расстояние d от точки до оси: M=md. При этом расстояние d берется со знаком «+» или «-» в зависимости от того, с какой стороны от оси находится точка.

Статический момент M системы n материальных точек m₁, m₂,…m_n, лежащих в одной плоскости с осью на расстояниях d₁,…d_n соответственно равен .

Ц ентр тяжести системы материальных точек на плоскости – это такая точка, что если в ней сосредоточить массы всех точек системы, то её статический момент относительно любой оси будет равен статическому моменту всей системы точек относительно той же оси.

Рассмотрим плоскую фигуру Р и предположим, что по ней распределена масса с поверхностной плотностью =(х;у) в любой точке М(х;у)Р. Разобьём Р на n произвольных частей Р₁,Р₂,…,P_n и в каждой P_i выберем произвольно точку N_i(u_i;v_i). Будем считать, что масса i-й части , и что она сосредоточена в точке N_i(u_i;v_i). Тогда статические моменты и всей фигуры P относительно Ox и Oy:

, .

Равенства тем точнее, чем мельче разбиение, следовательно,

, .

В правых частях - интегральные суммы для функций : y(х;у) и x(х;у), которые являются непрерывными. Следовательно, пределы интегральных сумм существуют и равны соответственно интегралам от этих функций. Значит,

, .

Обозначим (х_с;у_с) - координаты центра тяжести фигуры Р. Пусть m – ее масса. Тогда по определению центра тяжести: , . Отсюда

, .

Если фигура однородная (то есть (х;у)=const), то учитывая, что , получим

, .

П ример. Найти центр тяжести однородной плоской фигуры, ограниченной синусоидой y=sinx, осью Ox и прямой .

 Так как плоская фигура однородна, то используем последние формулы. Найдём площадь фигуры Р:

,

, , ,

. 
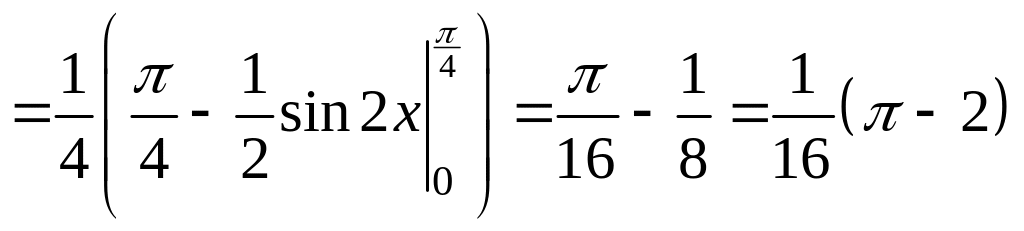