4. Двойной интеграл в полярных координатах

Если преобразование стоит в переходе к полярным координатам, то формула (6) примет вид:

.

Переход к полярным координатам эффективен, если уравнение границы области интегрирования или подынтегральная функция содержит выражение x²+y².

Если в состав подынтегральной функции или уравнения границы области входит сумма вида ax²+by² (a>0, b>0), то используют «обобщённую» полярную систему координат:

,

т огда , а .

Пример 1. Вычислить , где D- часть круга x²+y²=R², лежащая в I четверти.

 Перейдём к полярным координатам

Область . Следовательно,

. 

П ример 2. Найти площадь фигуры Р, ограниченной параболами y=ax², y=bx² (0<a<b) и гиперболами xy=p, xy=q (0<p<q).

 Площадь фигуры , но непосредственно вычислить этот интеграл трудно. Поэтому следует выполнить замену переменных.

Рассмотрим 2 семейства кривых: парабол y=ux² (или ) и гипербол xy=v. Чтобы каждое из них заполняло фигуру Р, достаточно взять какие u, v, которые удовлетворяют неравенствам aub, pvq. Через каждую точку фигуры Р проходит только одна парабола и только одна гипербола. Следовательно, эти два семейства кривых образуют сетку координатных линий.

Так как задание этих двух кривых (то есть параметров u и v) однозначно определяет точку фигуры Р, то u и v можно принять за криволинейные координаты точек фигуры Р: (*)

Область Р перейдет в прямоугольник Q: aub, pvq на плоскости uOv, т.к.

, ,

, .

Выразим из уравнений (*) x и y и найдем якобиан.

  

Тогда по формуле (5)

. 

§6. Приложения двойного интеграла

1. Площадь поверхности

Пусть поверхность S задана явным уравнением

z=f(x;y), (1)

причём проекция поверхности S на плоскость XOY – квадрируемая область Р, а функция f(x;y) определена, непрерывна и имеет непрерывные частные производные первого порядка на Р. Тогда функция f(x;y) будет дифференцируемой на Р, а поверхность S в каждой точке M(x₀;y₀;z₀) имеет касательную плоскость, уравнение которой

,

г де x, y, z – текущие координаты касательной плоскости, а x₀, y₀, z₀- координаты точки касания.

Задача. Найти площадь поверхности S.

Установим само понятие площади поверхности. Разобьём область Р на части . Построим на каждой из них, как на основании, цилиндрические столбики. Они разобьют поверхность на n частей: . В каждой части произвольно выберем точку , которой на частичной поверхности S_i будет соответствовать точка , где . Построим в точке касательную плоскость Т_i к поверхности S и нормаль к этой поверхности.

Каждый из цилиндрических столбиков вырежет на касательной плоскости Т_i фигуру, которую также обозначим Т_i. Если разбиение становится всё более мелким (0), то плоские фигуры Т_i будут приближаться к соответствующим частям S_i: . Тогда сумма площадей всех Т_i: .

Под площадью данной поверхности S понимают предел последней суммы при

, - диаметр .

Покажем, что этот предел существует и выясним, чему он равен.

Из курса геометрии известно, что площадь проекции плоской фигуры на плоскость равна произведению площади проектируемой фигуры на косинус острого угла между плоскостью проекции и плоскостью, в которой лежит проектируемая фигура.

Обозначим - острый угол между нормалью и осью Oz. Т.к. уравнение нормали к поверхности S в точке имеет вид

, то .

Вектор также является нормальным вектором поверхности. Тогда

,

где - единичный вектор оси ОZ.

Угол равен углу между касательной плоскостью и плоскостью XOY. - ортогональная проекция частичной фигуры , следовательно,  . Тогда

.

Эта сумма является интегральной суммой для функции

.

Т.к - непрерывная функция, то она интегрируема, следовательно,

 .

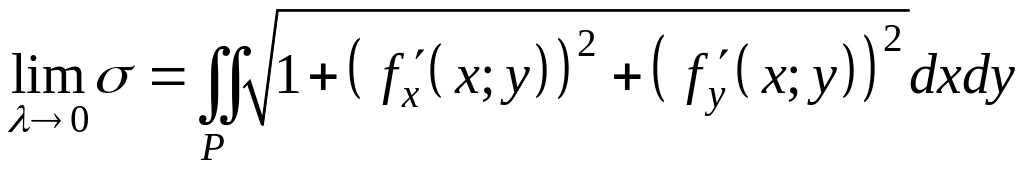Тогда .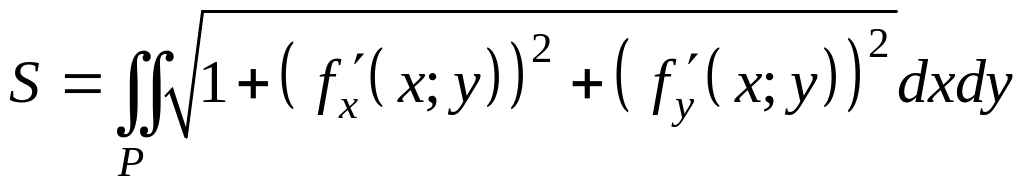

П ример. Вычислить площадь части параболоида , вырезанной цилиндром .

 Указанная поверхность симметрична относительно плоскостей XOZ и YOZ, т.е. состоит из четырёх одинаковых частей. Найдём площадь поверхности одной из них (например, лежащей в I октанте) и умножим на 4.

,

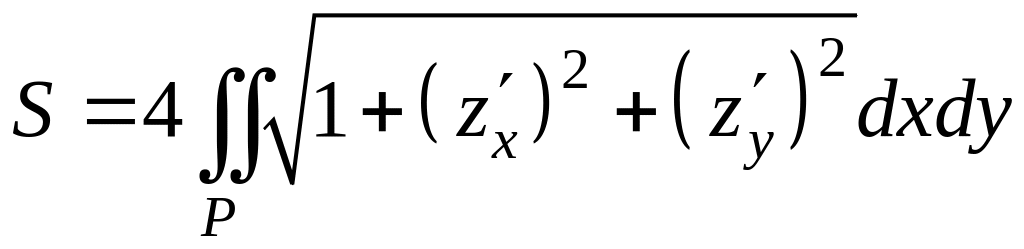Р – область интегрирования: четверть круга с центром в т.(0,0) и радиусом 1 в плоскости XOY.

Из уравнения поверхности получаем: , .

.

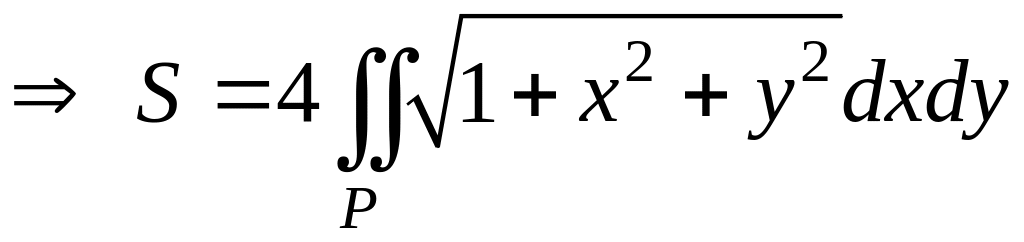Интеграл удобно вычислить в полярных координатах:

. 