2. Тройной интеграл в цилиндрических и сферических координатах

Как и для двойного интеграла, для тройного интеграла имеют место формулы перехода от прямоугольных координат к новым системам координат. Наиболее употребительные из них – цилиндрические и сферические.

I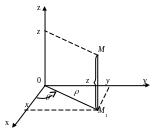 . Цилиндрические координаты

Пусть M₁ - проекция точки M на плоскость XOY, =OM₁- полярный радиус точки M₁, =xOM₁- полярный угол точки M₁, z – аппликата точки M. , , z называются цилиндрическими координатами точки M. . Обозначается M(;;z).

Связь с x, y, z: x=cos, y=sin, z=z.

Следовательно, преобразование тройного интеграла к цилиндрическим координатам происходит так же, как и преобразование двойного интеграла к полярным координатам.

Формула перехода к цилиндрическим координатам в тройном интеграле:

.

Если положить f(x;y;z)=1 всюду в (V), то

- объем тела (V) в цилиндрических координатах.

В ыражение называется элементом объема в цилиндрических координатах.

Пример 2. Вычислить объем кругового цилиндра высоты H с радиусом основания R.

 Поместим начало системы координат в центр нижнего основания конуса. Тогда 0R, 0<2, 0zH.

.

(известная формула элементарной геометрии). 

П ример 3. Вычислить объем тела, ограниченного сферой и параболоидом .

 Найдем проекцию линии пересечения сферы и параболоида на плоскость XOY. Для этого из уравнений выразим и решим систему:

,

,

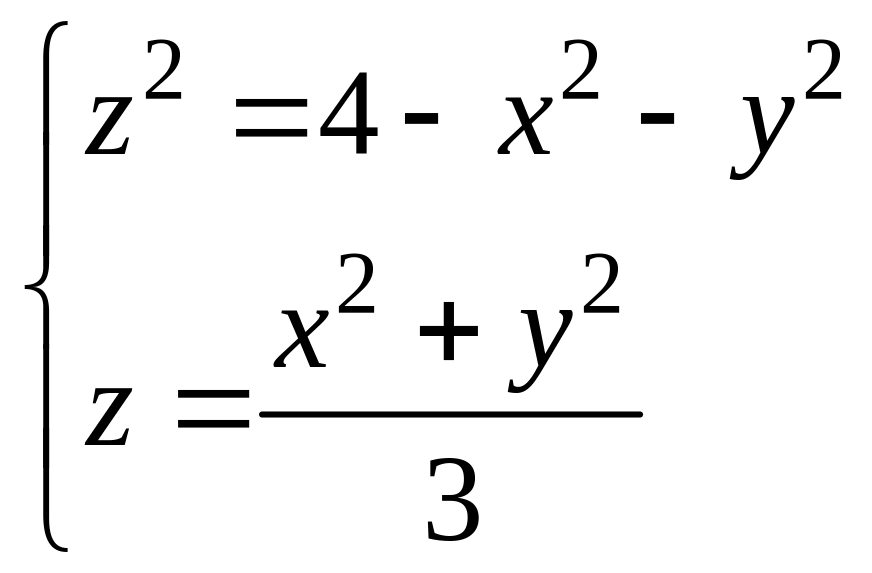
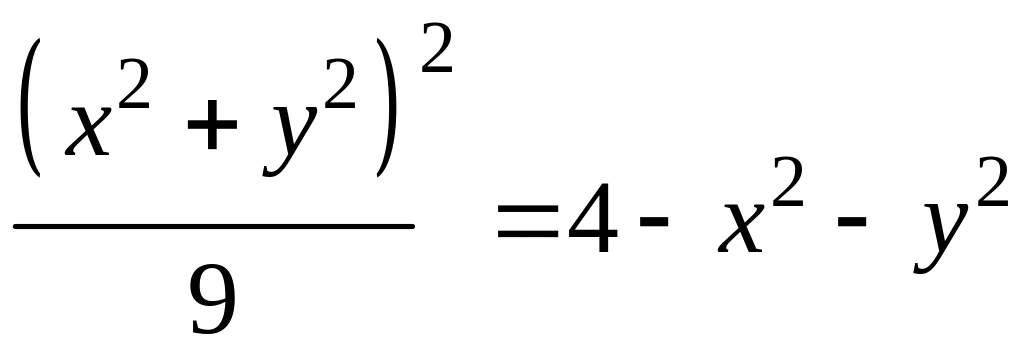или - не удовлетворяет условию .

Следовательно, линией пересечения поверхностей является окружность , при этом .

Т.к. тело симметрично относительно плоскостей XOY и YOZ, то можно вычислить объем тела , лежащего в I октанте и умножить на 4. Тогда .

Так как проекция тела на плоскость XOY – круг, то следует перейти к цилиндрическим координатам: x=cos, y=sin, z=z.

Преобразуем уравнения границ:

,

.

Уравнения границы проекции: .

Итак, в области : . Следовательно,

=

. 

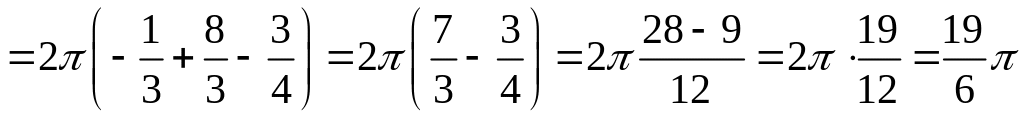I I. Сферические координаты

Сферическими координатами точки называются: ОМ= - расстояние от точки до начала координат, =xOM₁ - угол между Ox и проекцией отрезка на плоскость XOY, =zOM - угол между осью Oz и отрезком OM: М(;;), 0, 0<2, 0.

Связь с прямоугольными координатами:

z=cos (из zOM),

OM₁=sin (из zOM, zM=OM₁),

x=OM₁cos  x=sincos (из xOM₁),

y=OM₁sin  y=sinsin (из xOM₁, xM₁=Oy).

Итак, x=sincos, y=sinsin, z=cos.

. (Вычислить самостоятельно.)

Формула перехода в тройном интеграле к сферическим координатам:

.

Если положим здесь f(x;y;z)=1 всюду в ( ), то получим

- объем тела (V) в сферических координатах.

Выражение называется элементом объема в сферических координатах.

П ример 4. Вычислить объем шара радиуса R.

 Поместим начало системы координат в центр шара. Тогда 0R, 0<2, 0.

.

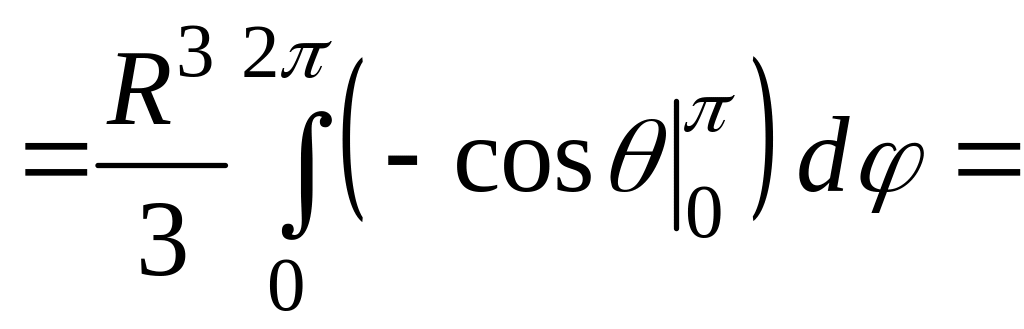
(известная из элементарной геометрии формула). 

36