4.1.7. Различение сигналов

Рассмотрим применение отношения правдоподобия для различения двух сигналов и как частный случай – обнаружение сигнала на фоне шумов. Положим, источник может находиться в двух состояниях и, характеризующихся двумя сигналамии, отличающимися друг от друга некоторыми параметрами, (например, амплитудой, фазой и т.д.).

На вход приемника поступает дискретная во времени аддитивная смесь одного из сигналов и шума

,

со значениями

,

шум распределён по нормальному закону с математическим ожиданием, равным нулю и известной дисперсией ,

.

Математическое описание сигналов экспериментатору известен, но неизвестно, какой из сигналов присутствует на входе приемника. В этой ситуации проверяются две альтернативные гипотезы -

: источник находится в состоянии , т.е. генерирует сигнал,

: источник находится в состоянии , т.е. генерирует сигнал.

На основании выборки экспериментатор должен вынести решениеилио состоянии источника информации.

Для решения задачи применим отношение правдоподобия, которое введено в разделе 3.

В примере 3.3 был получен логарифм отношения правдоподобия

(4.37)

при проверке двух альтернативных гипотез о состоянии источника ,. Все рассмотренные критерии, кроме минимаксного критерия, приводят к единому правилу решения - отношение правдоподобиясравнивается с порогом, зависящим от критерия. Отвлекаясь от типа применяемого критерия, обозначим этот порог черезС. По необходимости, будем заменять величину С соответствующим порогом согласно выбранному критерию.

Использовав нормальный закон распределения вероятности значений шума в дискретные моменты времени, был записан логарифм отношения правдоподобия в виде

(3.8)

Используя (4.37), запишем правило принятия решения

.

(4.38)

Преобразуем (4.38) в вид, удобный для анализа

, (4.39)

где .

Правая часть неравенства не зависит от сигнала на входе приемника. Она определяется априорно известными данными.

Величина 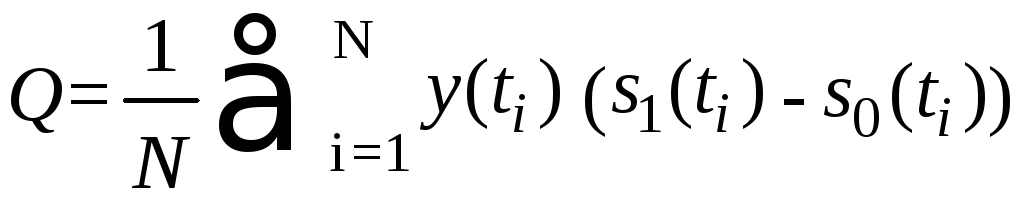- статистика, распределенная, согласно (3.8), по нормальному закону с параметрами, зависящими от состояния источника и шума:

,

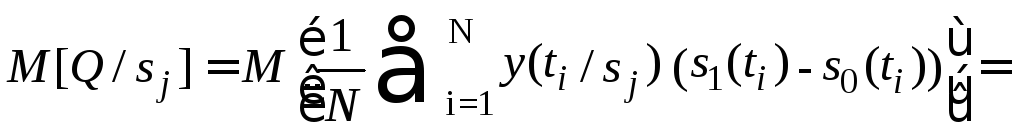(4.40)

=(4.41)

Как видно из (4.41), дисперсия величины Q не зависит от состояния источника на момент приема сигналов. Значимость критерия и мощность критерия определяются как

, (4.42)

. (4.43)

Если решается задача обнаружения сигнала, одно из состояний источника примем за наличие только шума, скажем состояние , т.е. сигнали на вход приемника поступает или шум, или смесь шума и сигнала. Реализация обрабатываемого сигналав задаче обнаружения примет вид

где - реализации шума,- реализации сигнала.

В этом случае формулы (4.38) – (4.43) примут вид

, (4.44)

, (4.45)

где .

Математическое ожидание и дисперсия величины вычисляются как

(4.46)

=.

(4.47)

Значимость критерия и мощность критерия вычисляются по формулам (4.48) и (4.49):

, (4.48)

(4.49)

На рисунке 4.2 изображены плотности распределения вероятностей величины при состояниях источникаи. Интервал значений () – критическая область – область, при попадании в которую значенийгипотезаотвергается, в то время как она верна.

Качество алгоритма обнаружения сигнала оценивается рабочей характеристикой приемника: – вероятность правильного обнаружения как функция вероятности ложной тревоги.