4.1.2. Минимаксный критерий

При использовании этого критерия априорной информацией является матрица потерь и функция правдоподобия. Вероятности , () состояния источника неизвестны. В этом случае средний рискневозможно вычислить. Но доступной информацией является условный риск:

(4.8)

Риски изависят от элементов матрицы потерьи от выбора критического подмножества.

Пусть заданы правила разбиения множествана подмножества. Для каждого правила имеются свои значения условных рисков и , . Для заданного правилавыберем из каждой пары условных рисков наибольший риск

,

В результате получим ряд значений . Из всех существующих рисков выберем тот, который даёт наименьшее значение: . Этому риску соответствует правилоиз множества правил разбиения множестваG. Критерий, обеспечивающий наименьший риск из наиболее возможных рисков, называется минимаксным критерием

(4.9)

Определяющим в этом критерии является способ разбиения множества значений на подмножества.

Пример. Случайная величина принимает значения 1 и 0 с вероятностью и 1-, соответственно. Производится два независимых испытания и в результате имеется выборка объёма. Наблюдателю неизвестно значение , но он предполагает, что вероятность равна либо 0.3, либо 0.5. Таким образом, имеются две гипотезы

, .

Генеральная совокупность образована из всевозможных реализаций:

Выберем правила разбиения множества (субъективно):

Матрица потерь имеет вид

.

Теперь, основываясь на методике минимаксного критерия, нужно выяснить, какое правило разбиения наилучше: или?

Рассмотрим правило .

Вероятности ошибок и вероятности правильных решений будут

,

,

,

Условный риск при разбиении по правилу и верности гипотезыравен

Условный риск при разбиении по правилу и верности гипотезыравен

Максимальное значение риска при разбиении будет равно

.

Рассмотрим правило .

Вероятности ошибок при разбиении по правилу будут

,

,

,

.

Условный риск при разбиении по правилу и верности гипотезыравен.

Условный риск при разбиении по правилу и верности гипотезыравен

Максимальное значение риска при разбиении по правилу будет равно

.

Из двух правил разбиения выберем то правило, которое обеспечивает минимальный условный риск .

Таким образом, наилучшим является правило разбиения .

4.1.3. Критерий максимума апостериорной вероятности

Для применения критерия максимума апостериорной вероятности априорно необходимо знать вероятности состояний источника ,таких, что+= 1, функции правдоподобия,.

Совместная вероятность состояния источника и регистрируемой выборки имеет вид

, j=0; 1. (4.10)

В этом выражении

- априорная вероятность того, что источник находится в состоянии ,j=0; 1.

- функция правдоподобия при состоянии источника .

- апостериорная⁴ вероятность – вероятность того, что источник находится в состоянии при условии , что выборка приняла значения.

Выразим апостериорные вероятности через составляющие выражения (4.10) и определенные состояния источника

, . (4.11)

В данном случае так же, как и при построении критерия Байеса, к выборочному подпространству отнесем только те выборки , которые обеспечиваютмаксимум апостериорной вероятности при условии, что источник находится в состоянии . Это является критерием разбиения выборочного пространства на подпространства и . В количественном соотношении этот критерий имеет вид

, (4.12)

т.е. вероятность того, что источник находится в состоянии больше, чем вероятность того, что источник находится в состояниипри одной и той же выборке, принадлежащей выборочному подпространству .

Этот критерий называется критерием максимума апостериорной вероятности. При нарушении неравенства (4.12) принимается гипотеза .

Из неравенства (4.12) и соотношений (4.11) следует

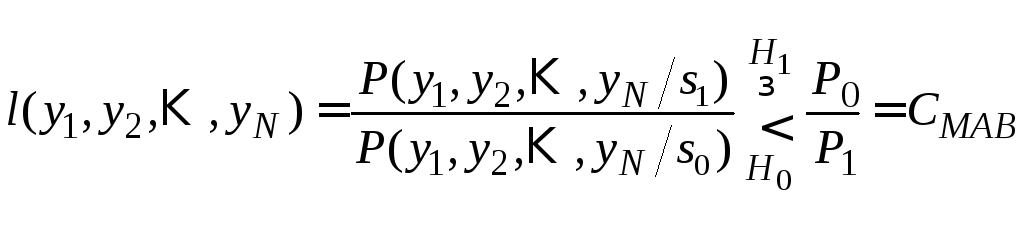. (4.13)

Если значения выборки принадлежат непрерывному множеству, то неравенство (4.13) приводится к виду

. (4.14)

Неравенства (4.13) и (4.14) являются правилами, реализующими критерий максимума апостериорной вероятности.

Если в критерии Байеса положить , то в качестве частного случая получимкритерий максимума апостериорной вероятности.