4. Критерии качества и правила принятия решений

Из-за действия шума возможны ошибки в принятии решений. Выборка может принадлежать подмножествуи примется решение о том, что источник находится в состоянии, хотя источник находился в состоянии. Последствия ошибок могут быть различны. В частности, можно построитьматрицу потерь, платежную матрицу (как меру потерь) при принятии гипотезы , в то время как источник был в состоянии, .

При неоднократном применении процедуры проверки гипотез с данным правилом можно вычислить математическое ожидание потерь

, (4.1)

где - условная вероятность попадания выборки в областьпри состоянии источника. Величинуназываютусловным риском для гипотезы . Если задано распределение состояний источника, то полные потери (риск) при заданном правилепринятии решений будут иметь вид:

(4.2)

Функция называетсясредней функцией риска. Способ разбиения выборочного пространства на подпространства, так чтобы функция рискаприняло минимальное значение,, называетсякритерием Байеса. Правило принятия решений, которое обеспечивает минимальное значение риска , будем называтьоптимальным по Байесу. Это минимальное значение средней функции риска называетсяриском по Байесу, а правило принятия решений в этом случае называется байесовским правилом принятия решений.

4.1. Проверка двухальтернативных гипотез

Рассмотрим критерии и правила проверки двухальтернативной гипотезы. Положим, источник имеет два состояния и. Потребителю неизвестно, в каком состоянии находится источник. Выдвигаются две гипотезы:

: источник находится в состоянии , т.е. генерирует сигнал,

: источник находится в состоянии , т.е. генерирует сигнал.

На основании выборки потребитель должен вынести решениеилио состоянии источника информации.

Разобьём множество на два подмножестваи. Если после проведенияизмерений выборка, принимаем решениео том, что источник находится в состоянии , а еслипринимаем решениео том, что источник находится в состоянии.

При проверке двухальтернативных гипотез принято классифицировать вероятности ошибок в зависимости от проверяемых гипотез.

—вероятность ошибки первого рода. В радиолокации она называется вероятностью ложной тревоги. В теории проверки статистических гипотез вероятность ошибки первого рода называется значимостью критерия.

—вероятность ошибки второго рода. В силу того, что подмножества G₀ и G₁ не пересекаются, имеем

—вероятность правильного решения о верности гипотезы H₀.

—вероятность правильного решения о верности гипотезы H₁ и называется мощностью критерия. В радиолокации она называется вероятностью правильного обнаружения.

Пользуясь функцией правдоподобия , запишем соответствующие вероятности в интегральной форме



Как видно из формул, вероятности ошибок зависят от правила разбиения множества на два подмножестваи.

4.1.1. Критерий Байеса

В качестве априорной информации наблюдатель должен знать матрицу потерь , функцию правдоподобия,, вероятности состояний источника,таких, что, т.е. источник информации должен находиться в одном из двух возможных состояний.

Запишем матрицу потерь ,

где , , ,, — потери при принятии гипотезы в то время, как источник находится в состоянии. Обычно — потери при правильных решениях должны быть меньше потерь из-за неправильных решений.

Вычислим средние условные потери (условные риски) при верности гипотез и

+

+

Безусловный риск (функция среднего риска) запишется как

Перепишем средний риск в виде, удобном для анализа,

(4.3)

В полученном выражении вероятности изависят от выбора подмножества, а вероятностьзависит от выбора подмножества.

В силу того, что подмножества идополняют друг друга доG, то достаточно указать, как выбирать , чтобы минимизировать. Областьназываетсякритической. Чтобы привести области интегрирования к одной области , произведем замену. Тогда средний рискбудет иметь вид

(4.4)

Из выражения (4.4) видно, для минимизации среднего риска необходимо иметь максимально положительное значение интеграла. Если подынтегральная функция будет принимать положительные значения на множестве , то значения интеграла будут неотрицательны. Принимая это во внимание, отберём из множествате значения, которые обеспечивают не отрицательность подынтегральной функции. Это множество значенийсоставляет подмножествоиз множества, т.е. в подмножествовключены точки которые удовлетворяют условию

или

. (4.5)

При вычислении среднего риска интегрирование производилось по области. Поэтому правилом принятия гипотезыбудет выполнение неравенства (4.5). Нарушение неравенства (4.5) говорит о том, что вероятность получить выборку фиксированного видапри состоянии источникабольше, по сравнению с вероятностью получить ту же самую выборку при состоянии источника . Поэтому при нарушении неравенства (4.5) гипотезуотвергают и более целесообразно считать правдоподобной гипотезу:.

Правая часть неравенства (4.5) постоянна и не зависит от выборки и это отношение , зависящее только от априорных сведений, называется порогом Байеса.

Левая часть неравенства (4.5) представляет отношение правдоподобия. Перепишем неравенство (4.5) в виде

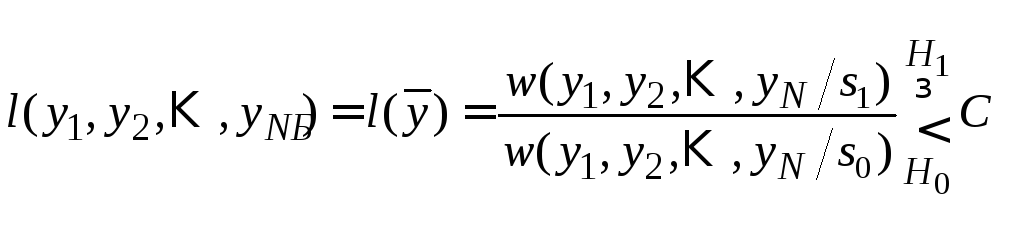, (4.6)

в котором символы иуказывают, какие гипотезы следует принять при выполнении соответствующего неравенства.

Если случайные величины независимы, отношение правдоподобия в неравенстве (4.6) примет вид

. (4.7)

Неравенство(4.7) является правилом обработки последовательности независимых наблюдений по критерию Байеса.